Loi arc sinus

En théorie des probabilités, les loi arc sinus est un ensemble de lois de probabilité à densité dont le support est un intervalle compact. Elles sont un cas particulier de la loi bêta. Les lois arc sinus sont des résultats des marches aléatoires linéaires (en dimension 1) modélisant le mouvement brownien. Plus précisément, elles modélisent le processus de Wiener.

Loi arc sinus
Densité de probabilité


Fonction de répartition

Paramètres	aucun
Support	$x\in [0,1]$
Densité de probabilité	$f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}$
Fonction de répartition	$F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)$
Espérance	${\frac {1}{2}}$
Médiane	${\frac {1}{2}}$
Mode	$x\in {]0,1[}$
Variance	${\tfrac {1}{8}}$
Asymétrie	$0$
Kurtosis normalisé	$-{\tfrac {3}{2}}$
Fonction génératrice des moments	$1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {2r+1}{2r+2}}\right){\frac {t^{k}}{k!}}$
Fonction caractéristique	${}_{1}F_{1}({\tfrac {1}{2}};1;i\,t)\$

Loi standard

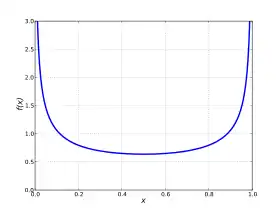
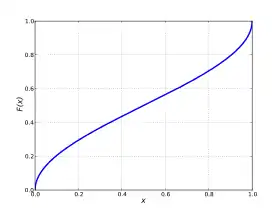
Une variable aléatoire X suit la loi arc sinus standard si sa fonction de répartition est donnée par :

F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)={\frac {\arcsin(2x-1)}{\pi }}+{\frac {1}{2}},\forall {x}\in [0;1]

pour $0 \leq x \leq 1$ , et dont la densité de probabilité est donnée par :

f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}

sur $]0 ; 1[$ . La loi arc sinus standard est un cas particulier de la loi bêta avec les paramètres $α = β = 1 / 2$ . Ainsi, si $X$ est de loi arc sinus standard alors $X\sim {\rm {Beta}}({\tfrac {1}{2}},{\tfrac {1}{2}}).$

Généralisation

Loi arc sinus – support borné



Paramètres	$-\infty <a<b<\infty \,$
Support	$x\in [a,b]$
Densité de probabilité	$f(x)={\frac {1}{\pi {\sqrt {(x-a)(b-x)}}}}$
Fonction de répartition	$F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {\frac {x-a}{b-a}}}\right)$
Espérance	${\frac {a+b}{2}}$
Médiane	${\frac {a+b}{2}}$
Mode	$x\in {]a,b[}$
Variance	${\tfrac {1}{8}}(b-a)^{2}$
Asymétrie	$0$
Kurtosis normalisé	$-{\tfrac {3}{2}}$

Support borné arbitraire

La loi peut être étendu à tout support borné $[a; b]$ par une simple transformation de la fonction de répartition

F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {\frac {x-a}{b-a}}}\right)

pour $a \leq x \leq b$ , la densité de probabilité est ainsi

f(x)={\frac {1}{\pi {\sqrt {(x-a)(b-x)}}}}

sur $] a; b [$ . Cette loi est notée $arcsinus(a, b)$ .

Paramètre de forme

La loi arc sinus standard généralisée sur $]0 ; 1[$ . avec pour densité de probabilité

f(x;\alpha )={\frac {\sin \pi \alpha }{\pi }}x^{-\alpha }(1-x)^{\alpha -1}

est également un cas spécial de la loi bêta de paramètres ${\rm {Beta}}(1-\alpha ,\alpha )$ . Le paramètre $α$ est appelé paramètre de forme. Lorsque $α = 1 / 2$ , cette loi est la loi arc sinus standard.

Propriétés

La loi arc sinus est stable par translation et par multiplication par un facteur positif :
- Si $X\sim {\operatorname {arcsinus} }(a,b)\ {\text{alors }}kX+c\sim {\operatorname {arcsinus} }(ak+c,bk+c)$ .
La loi arc sinus sur ]–1 ; 1[ mise au carré est la loi arc sinus sur ]0 ; 1[ :
- Si $X\sim {\operatorname {arcsinus} }(-1,1)\ {\text{alors }}X^{2}\sim {\operatorname {arcsinus} }(0,1)$ .

Relations avec d'autres lois

Si $U$ et $V$ sont des variables indépendantes et identiquement distribuées de loi uniforme continue sur $]-π ; π[$ , alors $sin(U)$ , $sin(2 U)$ , $-cos(2 U)$ , $sin(U + V)$ , et $sin(U - V)$ ont toutes la loi arc sinus standard.
Si $X$ est de loi arc sinus généralisée de paramètre de forme $α$ et avec pour support l'intervalle fini $[a; b]$ , alors ${\frac {X-a}{b-a}}\sim {\rm {Beta}}(1-\alpha ,\alpha )\$ .

Loi limite du dernier retour à l'origine

On considère la marche aléatoire $(S n)$ définie comme la valeur atteinte après $n$ lancers d'une pièce de monnaie équilibrée (pile = +1, face = -1). $T n$ est la variable aléatoire définie comme le dernier instant où $S$ a atteint 0 sur $[0 , 2 n]$ :

T_{n}=\max\{0\leq k\leq 2n,S_{k}=0\}

Alors la variable aléatoire $T n / S 2 n$ converge en loi vers la loi arc sinus.

Référence

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Arcsine distribution » (voir la liste des auteurs).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.