King effect
En statistique, économie et éconophysique, le King effect (ou effet roi) décrit le phénomène par lequel le meilleur membre voire les deux meilleurs membres d'une suite de valeurs apparaissent comme des données aberrantes. Ces deux meilleurs membres sont imprévisiblement grands parce qu'ils ne correspondent pas à la distribution statistique ou distribution de rangs auxquels tous les autres membres obéissent.
Les distributions suivent alors une distribution de la loi de puissance[2], qui est une fonction exponentielle étirée[1] - [3], ou une loi fractale parabolique.
L'effet Roi a été observé dans la distribution :
- de la taille des villes françaises (où le point représentant Paris est le « Roi », échouant ainsi à se conformer à l'exponentielle étirée[1]), et de façon similaire pour les autres pays possédant une ville principale telle que le Royaume-Uni (Londres), et le cas extrême de Bangkok (voir la liste des villes de Thaïlande) ;
- de la popularité des musiciens[3] (où Cliff Richard et Elvis Presley sont les données aberrantes qui ne peuvent s'inclure dans une exponentielle étirée) ;
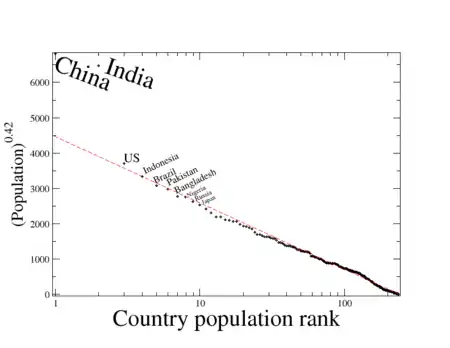
- de la population des pays (où seulement les points représentant la Chine et l'Inde échouent à se conformer à l'exponentielle étirée[1]).
Il est à noter cependant que l'effet Roi n'est pas limité aux données aberrantes situées à l'extrémité supérieure de la série : pour les classements selon un caractère indésirable, il existe également un Pauper effect (ou effet du Pauvre), avec un détachement similaire de valeurs extrêmes par rapport à la portion de la série de valeurs normalement distribuée.
Voir aussi
- Loi de Zipf
- Didier Sornette
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « King effect » (voir la liste des auteurs).
- (en) J. Laherrère et D. Sornette, Stretched exponential distributions in nature and economy: « fat tails » with characteristic scales
- (en) Arjun Jayadev, A power law tail in India's wealth distribution: Evidence from survey data
- (en) J.A. Davies, The individual success of musicians, like that of physicists, follows a stretch exponential