Jost Bürgi
Jost Bürgi ou Jobst Burgius ou Justus Byrgius (né le à Lichtensteig, décédé le à Cassel) est un horloger, concepteur ingénieux d'instruments de mesure, astronome et mathématicien suisse. Il a travaillé à Cassel au service du landgrave Guillaume IV de Hesse-Cassel et à Prague au service de l'empereur Rodolphe II et de ses successeurs.
Précurseur du calcul logarithmique, Jost Bürgi a collaboré avec l'astronome impérial Johannes Kepler.

| Naissance | |
|---|---|
| Décès |
(à 79 ans) Cassel |
| Activités |
| A travaillé pour |
Johannes Kepler (à partir de ) Rodolphe II du Saint Empire (à partir de ) Guillaume IV de Hesse-Cassel (à partir de ) |
|---|
Biographie
Les données biographiques concernant les 28 premières années de Bürgi ne sont pas sûres, en particulier son parcours de jeunesse qui est souvent décrit au conditionnel.
Jeunesse et formation
Jost Bürgi est né le à Lichtensteig, une petite bourgade non loin de Saint-Gall, en Suisse. Il est probablement le fils de Lienz[1] et petit-fils de Lienhart Bürgi[2], serruriers.
À Liechtensteig, il va à l'école, mais n'apprend pas le latin. Il s'exerce à la serrurerie avant de faire un apprentissage en orfèvrerie puis horlogerie, possiblement à Winterthour et Schaffhouse[3]. Entre 1572 et 1577, il voyage pour perfectionner son art, faisant probablement étape à Nuremberg, Augsbourg, Crémone et Strasbourg[4]. Au cours de son parcours de formation, il a pu rencontrer et bénéficier de la formation des frères Habrecht et de Conrad Dasypodius.
À la cour de Guillaume IV
En 1579, le landgrave Guillaume IV de Hesse-Cassel l'embauche en qualité d'horloger de la cour. Guillaume "le Sage" a fait construire à Cassel l'un des premiers observatoires d'Europe. Bürgi est chargé de la conservation des instruments scientifiques qu'il entretient et perfectionne. Il y pratiquera lui-même l'astronomie et y travaillera en compagnie de Christophe Rothmann (de) à partir de 1584 et Nicolaus Reymers (Ursus) en 1586-87[4].
En 1591, Jost Bürgi épouse une fille du pasteur de Felsberg, David Bramer. Ce dernier décède la même année laissant un orphelin de 3 ans, Benjamin Bramer (de) que le jeune couple va adopter. Bürgi assurera l'éducation de son beau-frère et lui transmettra ses connaissances en astronomie et en mathématiques plus particulièrement. Benjamin Bramer deviendra l'assistant de Bürgi et il travaillera à ses côtés jusqu'en 1611[5].
Peu avant sa mort en 1592, Guillaume IV accepte la demande de l'empereur Rodolphe II de faire venir Bürgi à Prague pour lui livrer un globe céleste muni d'un mécanisme qui simule les mouvements des planètes[6]. Lors de ce voyage, Bürgi présente également son Fundamentum Astronomiae (voir section Mathématiques) à l'empereur. De retour à Cassel, il reste au service de Maurice l'Éclairé qui succède à son père, mais il reviendra à Prague en 1604, nommé horloger de l'empereur avec l'assentiment de Maurice[6].
Horloger impérial
À Prague, Rodolphe II met à la disposition de son horloger un atelier et deux assistants[7].
Jost Bürgi est amené à travailler avec l'astronome impérial Johannes Kepler qui reconnaît ses compétences et son habileté en mathématiques. Ils collaboreront jusqu'à la mort de Rodolphe (1611). Après le décès à Cassel de sa première épouse, Bürgi se remarie le avec Catharina Braun[7]. Le couple n'aura pas d'enfant.
Les successeurs de Rodolphe, Matthias Ier et Ferdinand II siègeront à Vienne, mais Jost Bürgi restera à Prague avec son titre d'horloger impérial, retournant épisodiquement à Cassel, notamment en 1617, 1622 et en 1631 pour la dernière fois avant d'y décéder le [7].
Œuvre
Horlogerie

En 1580, Bürgi construit sa première horloge-globe céleste à Cassel[7].
En 1584, il réalise une horloge astronomique pour l'observatoire de Cassel munie d'un échappement à battement en croix et d'un remontoir automatisé à trois mois[8]. Ces innovations apportent un gain de précision considérable. L'horloge indique et bat la seconde. Elle doit contribuer à la qualité des observations astronomiques.
Plus tard, Bürgi construit d'autres horloges-globe céleste, chacune amenant de nouveaux perfectionnements. L'une d'entre-elles est exposée au CNAM à Paris[9].
Entre 1622 et 1627, il construit pour l'empereur Ferdinand II son chef-d'œuvre, l'horloge de Cristal, actuellement exposée au Kunsthistorisches Museum de Vienne[10] Il s'agit d'une horloge astronomique de table qui présente son mécanisme et ses éléments astronomiques par transparence.
Instruments scientifiques

Son employeur, le landgrave avait confié à Bürgi la conservation de ses instruments scientifiques (astrolabes, globes, etc.) ; c'est en les réparant que Bürgi réfléchit aux moyens de les perfectionner. Outre des horloges et ses globes, il a fabriqué un compas de réduction, des sphères armillaires, des sextants[11] un goniomètre et un pantographe.
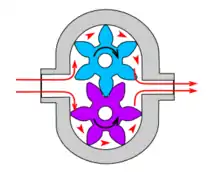
En 1604, Bürgi construit un prototype d'une pompe à engrenages imaginée par Kepler[12] (voir figure).
Dès 1610, l'atelier de Bürgi produit des instruments d'observation optiques. La première lunette astronomique pragoise est réalisée par son assistant, Hermann Stolle[13].
Astronomie

Guillaume IV avait entrepris de dresser un catalogue d'étoiles avant son accession au pouvoir. Jost Bürgi et Christophe Rothmann devaient le seconder et poursuivre ce travail. La précision des observations était tributaire de la bonne mesure des angles et du temps. Bürgi y contribuait par la qualité de ses instruments (voir paragraphes précédents). Le catalogue Grosses Hessiches Sternverzeichnis (1587) fut complété par les données de 383 étoiles supplémentaires[14].
Vers 1587, Bürgi construisit pour Reymers un planétaire conforme à la cosmologie géo-héliocentrique que préconisait ce dernier (voir Nicolas Raimarus Ursus). En retour, Reymers traduisit en allemand le De revolutionibus orbium coelestium de Nicolas Copernic à l'attention de Bürgi qui ne lisait pas le latin[15] - [16].
Plus tard, Bürgi étudia les trajectoires de la Terre et de la Lune pour mettre au point l'horloge de 1591 qui intégrait les anomalies de leurs mouvements selon le modèle copernicien[17].
Les travaux astronomiques de Bürgi ne sont pas consignés par des écrits, mais ils sont concrétisés par des réalisations techniques : le globe céleste mécanisé de 1594 exposé au Musée national de Zurich[18] présente 1026 étoiles regroupées en 47 constellations. La voûte céleste est ainsi vue de l'extérieur donnant aux constellations un dessin symétrique de leur aspect habituel. (voir figure)
À Prague, Jost Bürgi a travaillé en étroite collaboration avec Johannes Kepler de 1604 à 1611. C'est à cette période que Kepler a résolu le problème de la trajectoire de Mars et publié son Astronomia nova. Les biographes conjecturent sur les contributions de Bürgi à l'élaboration des lois de Kepler sur le mouvement elliptique des planètes[19]. En l'absence d'écrits, il est difficile de faire la part des choses, mais les techniques de calcul développées par Bürgi ont sans doute été utiles à Kepler.
Selon Staudacher, Bürgi a pu fournir une assistance technique lors des observations, notamment lors de l'apparition de la supernova de 1604 à un Kepler atteint de myopie notoire[20].
Mathématiques
Les travaux de Bürgi en mathématiques sont restés longtemps ignorés ou mal connus à défaut d'avoir été publiés. La découverte, en 2013, de son manuscrit Fundamentum Astronomiae[21] permet d'en savoir un peu plus sur ses méthodes[22]. Il a développé des techniques de calcul originales en trigonométrie et en calcul logarithmique qui font l'objet d'études récentes (2e décennie du XXIe siècle)[23].
Trigonométrie
Bürgi est l'auteur d'une table de sinus (Canon Sinuum) donnant les valeurs avec huit chiffres sexagésimaux suivant un pas de deux secondes d'arc, dont Kepler vantait la précision[24] mais qui est probablement perdue[25]. En revanche, le Fundamentum Astronomiae présente le Kunstweg ou habile démarche que Nicolaus Reymers attribue à Bürgi[26] : il s'agit d'un algorithme itératif qui permet de calculer les sinus des angles de mesures .
À la fin du XVIe siècle, de telles tables étaient utilisées non seulement pour la trigonométrie, mais aussi pour la pratique des multiplications ou divisions par la méthode de prostaphérèse dont Bürgi, Reymers et Tycho Brahe étaient des adeptes.
Logarithmes
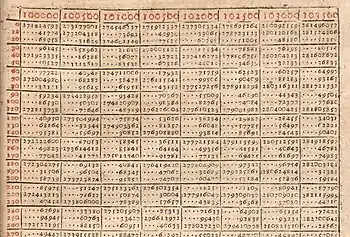
Jost Bürgi pratiquait une forme de calcul logarithmique avant même que le terme logarithme ne fût inventé par John Napier (Neper) (Mirifici logarithmorum canonis descriptio…, 1614). Au XVIe siècle des mathématiciens parmi lesquels Michael Stifel avaient déjà remarqué que la juxtaposition de suites arithmétiques et géométriques permettaient dans certains cas d'effectuer des additions en lieu et place de multiplications[27]. Bürgi a repris et développé ce principe pour élaborer une Table de progressions arithmétique et géométrique[28] avec le souci d'obtenir un résultat précis quels que soient les nombres à multiplier.
Sa table met en correspondance une suite arithmétique de nombres rouges et une suite géométrique de nombres noirs (voir figure).
La suite des nombres rouges est et la suite des nombres noirs est . Les noirs sont arrondis à l'entier le plus proche.
La table est présentée sur 58 pages : les nombres noirs de Bürgi vont de à avec plus de 23 000 valeurs intermédiaires, les nombres rouges allant de à .
Pour multiplier deux nombres noirs et , il suffit d'additionner les nombres rouges correspondants et puis de lire dans la table le nombre noir correspondant à la somme : il donne la valeur du produit à un déplacement de virgule près.
La graduation des rouges de 10 en 10 permet de faire des interpolations si l'on veut encore gagner en précision.
Comme les autres tables de logarithmes, la table des progressions de Bürgi permet également de faire rapidement des divisions ou des extractions de racines carrées ou cubiques[29].
Jost Bürgi pratiquait ce genre de calculs dès le début du XVIIe siècle[30]. Pour certains historiens, Neper et Bürgi sont les co-inventeurs des logarithmes[31] - [32], alors que d’autres font une distinction entre la fonction logarithme de Neper et les antilogarithmes de la table de Bürgi où les nombres noirs sont calculés en fonction des rouges.
La démarche de Bürgi dans le développement de cette technique est originale et indépendante des travaux de Neper dont il n'a eu connaissance qu'après leur publication (1614). Encouragé par Johannes Kepler, Bürgi fit imprimer sa table à Prague en 1620 sous le titre complet : Aritmetische vnd Geometrische Progress Tabulen, sambt gründlichem unterricht, wie solche nützlich in allerley Rechnungen zugebrauchen, vnd verstanden werden sol (Tables de progressions arithmétique et géométrique, accompagnée d'un enseignement fondamental sur la manière de les comprendre et de les utiliser pour toutes sortes de calculs).
Pour des raisons à préciser, les premières éditions connues de cette table ne comportaient que la première partie, alors que l'enseignement ne fut apparemment publié qu'en 1856 par H. Gieswald[33]. Privées de leur mode d'emploi, les tables de Bürgi ne furent guère utilisées.
Hommages
Les compétences de Jost Bürgi ont été reconnues par ses contemporains : le landgrave Guillaume écrivait à Tycho Brahe : "..il est capable d'innovations tel un nouvel Archimède."
Selon Willebrord Snell, "c'est une personnalité extraordinaire, à la fois brillant horloger, astronome compétent et excellent mathématicien, une combinaison unique dans l'histoire de l'horlogerie."
Dans ses Tables rudolphines, Kepler écrivait en 1627 : "m'aidant dans les calculs, Justus Byrgius a été conduit à ces mêmes logarithmes bien des années avant l'apparition du système de Napier ; mais étant un homme indolent, et très peu communicatif, au lieu d'élever son enfant pour le bien public, il l'a abandonné à la naissance ."
Il rend hommage à l'innovateur en mathématiques tout en regrettant sa réticence à publier sans doute due à sa mauvaise maîtrise du latin.

En 1935, l'Union astronomique internationale nomma Byrgius un cratère lunaire en hommage à Jost Bürgi. De même un astéroïde de la ceinture principale découvert en 1977 est recensé sous l'appellation (2481) Bürgi.
Dans sa ville natale de Lichtensteig, la mémoire de Jost Bürgi est entretenue : le site Internet www.alprhein.ch[34] lui est dédié, tenu à jour par l'enthousiaste biographe Fritz Staudacher et un symposium quasi-annuel est consacré à la redécouverte de l'œuvre de Jost Bürgi[35].
À Cassel, où il est décédé, sa sépulture n'existe plus mais une plaque honore sa mémoire au cimetière "Altstädter Friedhof"[4].
Sur le Johannes Kepler Denkmal, un monument érigée en 1870 sur la place du marché de Weil der Stadt, une statue de bronze de Kepler est installée sur un piédestal de grès[36]. Quatre autres personnages sont également représentés, qui ont eu une influence sur le parcours de Kepler : Jost Bürgi se trouve là en compagnie de Nicolas Copernic, Michael Maestlin et Tycho Brahe. Sa statue en bronze le présente tenant une sphère armillaire dans sa main gauche.
Bibliographie et liens
- (de) Ludwig Oechslin : Jost Bürgi, Luzern, 2000
- (de) Ludwig Oechslin : Der Bürgi-Globus : Technik und Kultur, Zürich : Schweizerisches Landesmuseum, 2000
- (de) Jost Bürgi: Aritmetische vnd Geometrische Progress Tabulen, sambt gründlichem vnterricht, wie solche nützlich in allerley Rechnungen zugebrauchen, vnd verstanden werden sol, Prag, 1620, Bayerische Staatsbibliothek.
- (de) H. Gieswald : Justus Byrg als Mathematiker u. dessen Einleitung in seine Logarithmen, 1856, version en ligne sur Google-books.
- (de) Fritz Staudacher[37] : Jost Bürgi, Kepler und der Kaiser - Uhrmacher, Astronom, Mathematiker, Instrumentenbauer, Erz-Metallurgist. (4e édition), NZZ Libro, Zürich, 2018.
- (en) F. Cajori : Algebra in Napier's day and alleged prior inventions of logarithms (1915), Napier Tercentenary Memorial Volume (C. G. Knott ed.), Longmans, Green & Co., Londres.
- (en) Denis Roegel : Bürgi's "Progress Tabulen" (1620): logarithmic tables without logarithms, 2010, http://www.loria.fr/~roegel/locomat.html
- (en) Denis Roegel, A preliminary note on Bürgi’s computation of the sine of the first minute, 2016, https://hal.inria.fr/hal-01316358/document
- (en) Kathleen Clark, Jost Bürgi's Aritmetische und Geometrische Progreß Tabulen (1620), Birkhaüser, 2015. Extraits sur Google-books
- (en) Menso Folkerts, Dieter Launert, Andreas Thom, Jost Bürgi’s Method for Calculating Sines, Historia Mathematica, 2015.
- Histoire des logarithmes et des exponentielles.
- Pierre Mesnage, Un chef-d'œuvre de Jost Bürgi au Conservatoire des Arts et Métiers de Paris, www.Horlogerie-Suisse.com, 2013, accessible en ligne.
Liens externes
- (de) Biographie
- (de) Article dans Wikidesia
Notes et références
- Neuschwander-Naon, Jost Bürgi, Dictionnaire historique de la Suisse, 2005.
- O'Connor-Robertson, Jost Bürgi, Mac-Tutor, University of St-Andrews, Écosse, 2010.
- Fritz Staudacher, Bürgis's Timeline sur www.alprhein.ch.
- O'Connor-Robertson
- (de) Moritz Cantor, « Burgi: Jobst B. », dans Allgemeine Deutsche Biographie (ADB), vol. 3, Leipzig, Duncker & Humblot, , p. 604-606
- Cantor, ADB
- Staudacher
- Fritz Staudacher, Jost Bürgi n’a pas seulement inventé la seconde, Société Suisse de Physique 2009. (article en ligne).
- Pierre Mesnage, Un chef-d'œuvre de Jost Bürgi au Conservatoire des Arts et Métiers de Paris, www.Horlogerie-Suisse.com, 2013.
- Wiener Kristalluhr, Kunsthistorisches Museum, Vienne. (Image et notice en ligne)
- Voir Musée National Technique de Prague, Bürgiho sextant
- Fritz Staudacher, Jost Bürgi Zeittafel
- ibid.
- Kathleen Clark, Jost Bürgi's Aritmetische und Geometrische Progreß Tabulen (1620): Edition and Commentary, Birkhaüser 2015, page 5.
- Kathleen Clark, page 6.
- C'est la première traduction en allemand de l'ouvrage de Copernic, connue sous le nom de Manuscrit de Graz
- Clark, page 6.
- Staudacher, Bürgi-symposium, en ligne
- Voir, par exemple Kathleen Clark, Jost Bürgi's Aritmetische und Geometrische Progreß Tabulen..., page 7.
- Staudacher, Jost Bürgi synoptische Zeittafel lien vers le .pdf.
- Bibliothèque universitaire de Wrocław, Menso Folkerts 2013.
- Bürgi developed a very ingenious collection of algorithms and obviously had a very deep sense of Numbers (Denis Roegel, A preliminary note on Bürgi’s computation of the sine of the first minute, 2016, hal-01316358.
- Études de Denis Roegel, Kathleen Clark, Menso Folkerts-Dieter Launert-Andreas Thom, voir #Bibliographie et liens
- Voellmy, Bürgi und die Logarithmen, Elemente der Mathematik, p. 13. La précision du Canon Sinuum de Bürgi ne peut cependant pas être évaluée objectivement tant que l'on ne le retrouve pas.
Voir Denis Roegel, A tentative reconstruction of Bürgi’s sine table at 2 intervals (ca. 1600), 2016. hal01316360 - Cf. Kathleen Clark, Jost Bürgi's Aritmetische und Geometrische Progreß Tabulen (1620), Birkhaüser, coll. « Science Networks. Historical Studies n°53 », (ISBN 9781493931613), « A Brief Biography of Jobst Bürgi », p. 8, note 14.
- Menso Folkerts, Dieter Launert, Andreas Thom, Jost Bürgi’s Method for Calculating Sines, Historia Mathematica, 2015, pages 8-10.
- par exemple
- Jost Bürgi Aritmetische und Geometrische Progress Tabulen…, Prague 1620.
- Pour une étude précise, voir Denis Roegel : Bürgi's Progress Tabulen (1620): logarithmic tables without logarithms, 2010, http://www.loria.fr/~roegel/locomat.html (en anglais).
- Dès 1588, selon Lutstorf - Walter (Schriftenreihe der ETH-Bibliothek, Nr. 28. Zürich 1992), mais selon Denis Roegel, ce serait une mauvaise interprétation d'une citation de Reymers (Ursus). Roegel préconise plutôt que Bürgi aurait développé sa table de progressions à partir de son arrivée à Prague (1603). Voir sa note de bas de page détaillée dans Bürgi's "Progress Tabulen"..., (Denis Roegel 2010), pages 8-10.
- Voir à ce sujet Klaus Truemper, The Daring Invention of the Logarithm Tables, Leibniz Company 2020, page 97 : Who inventend Logarithms ?.
- André Bonnet : Neper a-t-il inventé les logarithmes népériens ?, APMEP n°524|2017, pages 87-89, (voir en ligne).
- H.Gieswald, Justus Byrg als Mathematiker u. dessen Einleitung in seine Logarithmen, 1856.
- (de) « Die Renaissance Jost Bürgis », sur alprhein.ch (consulté le ).
- (de) « Internationales Jost Bürgi symposium », sur www.jostbuergi.com.
- August von Kreling, Johannes Kepler Denkmal, Weil der Stadt, Marktplatz, images en ligne.
- « www.alprhein.ch », sur bluewin.ch (consulté le ).













