Intégrale d'Itō
L'intégrale d'Itô, appelée en l'honneur du mathématicien Kiyoshi Itô, est un des outils fondamentaux du calcul stochastique. Elle a d'importantes applications en mathématique financière et pour la résolution des équations différentielles stochastiques.
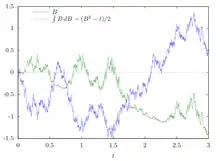
Elle généralise de façon stochastique l'intégrale de Stieltjes. L'intégrande H et l'intégrateur sont tous deux des processus stochastiques :
où H est un processus carré-intégrable localement adapté au filtre (au sens probabiliste) généré par X[1], qui est un mouvement brownien ou, de façon plus générale une semi-martingale. Le résultat de l'intégration, Y, est aussi un processus stochastique.
Description
Il s'agit d'une intégrale définie de façon similaire à l'intégrale de Riemann comme limite d'une somme de Riemann. Si on se donne un processus de Wiener (ou mouvement brownien) ainsi que un processus stochastique adapté à la filtration naturelle associée à , alors l'intégrale d'Itô
est définie par la limite en moyenne quadratique de
lorsque le pas de la partition de tend vers 0.
Ces sommes, considérées comme des sommes de Riemann-Stieltjes pour chaque chemin du mouvement brownien donné, ne convergent pas en général ; la raison en est que le mouvement brownien n'est pas à variations bornées. L'usage de la convergence quadratique est le point essentiel de cette définition.
Propriétés
Avec les notations précédentes, le processus stochastique Y défini, pour t réel positif, par , est une martingale. En particulier, son espérance est constante.
D'autre part, on a la propriété dite d'isométrie: . Cette dernière intégrale est « classique », c'est-à-dire qu'elle est une intégrale au sens de Riemann par rapport à la variable s.
Notes et références
- Revuz et Yor 1999, Chapter IV.
Bibliographie
- (en) Daniel Revuz et Marc Yor, Continuous martingales and Brownian motion, Berlin, Springer, (ISBN 3-540-57622-3)
Articles connexes
- Processus d'Itô
- Lemme d'Itô
- Calcul stochastique
- Intégrale de Stratonovich

![B:[0,T]\times \Omega \to {\mathbb {R}}\,](https://img.franco.wiki/i/842499692791290e9c4ad3dc4188bac6a8e6bbfd.svg)
![X:[0,T]\times \Omega \to {\mathbb {R}}](https://img.franco.wiki/i/5b00de44703312aa78ba1b270e89fc4a4481520b.svg)




![[0,T]](https://img.franco.wiki/i/35ccef2d3dc751e081375d51c111709d8a1d7ac6.svg)

