Hyperélasticité

Si le matériau est isotrope, il est possible de développer les lois de comportement grâce aux invariants des tenseurs de dilatation :

${\displaystyle {\mathbf {\sigma }}=2{\Biggl (}{\Biggl (}{\partial W \over \partial I_{1}}+I_{1}{\partial W \over \partial I_{2}}{\Biggr )}{\mathbf {B}}-2{\partial W \over \partial I_{2}}{\mathbf {B}}^{2}-{\partial W \over \partial I_{3}}I_{3}{\mathbf {I}}d{\Biggr )}}$

${\displaystyle {\mathbf {\pi }}=2{\Biggl (}{\Biggl (}{\partial W \over \partial I_{1}}+I_{1}{\partial W \over \partial I_{2}}{\Biggr )}{\mathbf {I}}d-{\partial W \over \partial I_{2}}{\mathbf {C}}-{\partial W \over \partial I_{3}}I_{3}{\mathbf {C^{-1}}}{\Biggr )}}$

Avec ${\displaystyle I_{1}=tr({\mathbf {C}})}$, le premier invariant

${\displaystyle I_{2}={1 \over 2}(tr({\mathbf {C}})^{2}-tr({\mathbf {C}}^{2}))}$, le second invariant

${\displaystyle I_{3}=det({\mathbf {C}})}$, le troisième invariant.

Si, de plus, le matériau est incompressible (${\displaystyle I_{3}=1}$), il est possible de réécrire ces équations en introduisant le multiplicateur de Lagrange noté p, assimilable à la pression hydrostatique, tel que :

${\displaystyle {\mathbf {\sigma }}=2{\Biggl (}{\Biggl (}{\partial W \over \partial I_{1}}+I_{1}{\partial W \over \partial I_{2}}{\Biggr )}{\mathbf {B}}-2{\partial W \over \partial I_{2}}{\mathbf {B}}^{2}-p{\mathbf {I}}d{\Biggr )}}$

${\displaystyle {\mathbf {\pi }}=2{\Biggl (}{\Biggl (}{\partial W \over \partial I_{1}}+I_{1}{\partial W \over \partial I_{2}}{\Biggr )}{\mathbf {I}}d-{\partial W \over \partial I_{2}}{\mathbf {C}}-p{\mathbf {C^{-1}}}{\Biggr )}}$

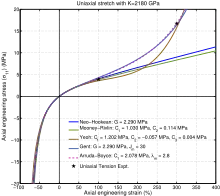
Dans l’approche dite « phénoménologique »[2], on cherche à décrire le comportement macroscopique de matériau sans nécessairement en comprendre les fondements physiques. Mooney (1940) fut le premier à proposer un potentiel d’énergie de déformation à partir des invariants du tenseur des dilatations de Cauchy-Green. Rivlin (1948) en a donné une expression simplifiée donnant le modèle « Néo-hookéen », puis une forme généralisée grâce à la décomposition en série de Taylor. Par la suite, plusieurs autres auteurs ont apporté des modèles phénoménologiques de plus en plus sophistiqués : Ogden, Gent, Yeoh, Marlow pour ne citer qu'eux. Les expressions de ces modèles sont données à partir d'invariants (${\displaystyle I_{1},I_{2},I_{3}}$) ou d'élongations principales (${\displaystyle \lambda _{1},\lambda _{2},\lambda _{3}}$). Rappelons qu’il est nécessaire de soustraire 3 à chaque invariant (resp. à chaque somme des élongations principales) afin d’assurer que la densité d’énergie de déformation soit nulle lorsque le matériau n’est pas sollicité, c'est-à-dire lorsque les invariants (resp. la sommes des élongations principales) sont égaux à 3.

${\displaystyle W(I_{1})=C_{0}(I_{1}-3)}$ où ${\displaystyle C_{0}}$ est le module d'élasticité du matériau dont la dimension est celle d'une contrainte

Le modèle de Rivlin généralisé[3] est donné par :

${\displaystyle W(I_{1},I_{2})=\sum _{i,j}^{N}C_{ij}(I_{1}-3)^{i}(I_{2}-3)^{j}}$

Un cas particulier est donné par le modèle de Mooney-Rivlin dans le cas où ${\displaystyle N=1}$ et ${\displaystyle i\neq j}$

${\displaystyle W(I_{1},I_{2})=C_{10}(I_{1}-3)+C_{01}(I_{2}-3)}$

où les ${\displaystyle C_{ij}}$ sont les modules d'élasticité du matériau

Contrairement au modèle Néo-hookéen et de Mooney-Rivlin qui montre une certaine linéarité en grande déformation, le modèle de Gent (en) reproduit correctement le durcissement important des élastomères avant rupture dû à la limite d'extensibilité des chaînes macromoléculaires[4]. Gent a imaginé une densité d'énergie de déformation présentant une singularité quand le premier invariant atteint une valeur limite notée ${\displaystyle I_{m}}$

${\displaystyle W(I_{1})=-\mu (I_{m}-3).ln{\Bigl (}1-{I_{1}-3 \over I_{m}-3}{\Bigr )}}$

Les paramètres de ce modèle sont donc ${\displaystyle \mu }$, module d'élasticité, et ${\displaystyle J_{m}=I_{m}-3}$.

Représentation graphique de différents modèles hyperélastiques.

Le modèle d'Ogden pose[5] : ${\displaystyle W(\lambda _{1},\lambda _{2},\lambda _{3})=\sum _{i=1}^{N}{\mu _{i} \over \alpha _{i}}(\lambda _{1}^{\alpha _{i}}+\lambda _{2}^{\alpha _{i}}+\lambda _{3}^{\alpha _{i}}-3)}$

où ${\displaystyle \alpha _{i}}$ et ${\displaystyle \mu _{i}}$ sont les paramètres du modèle. Contrairement aux autres modèles, ces paramètres n'ont pas de signification physique.

Le modèle de Yeoh pose[6] : ${\displaystyle W(I_{1},I_{2})=C_{10}(I_{1}-3)+C_{20}(I_{2}-3)^{2}+C_{30}(I_{1}-3)^{3}}$

où les ${\displaystyle C_{ij}}$ sont les modules d'élasticité du matériau.

Dans l’approche statistique, il est question de reproduire le comportement mécanique macroscopique par des considérations microstructurales physiquement fondées. On distingue les modèles gaussiens et non-gaussiens. Flory est en 1953 le premier à proposer un modèle statistique pour décrire le comportement des polymères en utilisant une répartition gaussienne des chaînes, c’est-à-dire que la longueur des chaînes est supposée suivre une loi normale. Il considère que l’entropie du réseau est la somme des entropies élémentaires des chaînes constitutives, que la longueur de chaque chaîne varie dans le même rapport que les dimensions du milieu macroscopique et que la déformation est isochore (sans variation de volume). En prenant en considération toutes ces hypothèses physiques, une densité d’énergie de déformation est définie en fonction des trois élongations principales :

${\displaystyle W={nkT \over 2}(\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}-3)}$

où n est le nombre de chaînes par unité de volume, k la constante de Boltzmann et T la température absolue.

On remarque premièrement qu’en posant ${\displaystyle C_{0}={nkT \over 2}}$ et en remplaçant la somme des carrés des élongations principales par le premier invariant du tenseur des dilations, on retrouve le modèle néo-hookéen. Le modèle de Flory ne s’avère précis que pour les petites déformations au même titre que le modèle néo-hookéen. De plus, la répartition gaussienne suppose que les chaînes moléculaires puissent atteindre une longueur infinie, ce qui est physiquement impossible. C’est la raison pour laquelle la théorie statistique à répartitions non-gaussienne a vu le jour. Ces derniers améliorent les prédictions pour une large gamme de déformation. Le premier modèle non-gaussien a été introduit par Kuhn et Grun (1942) décrivant l’élasticité d’une chaîne isolée composée de N monomères, tous de longueur L . La longueur initiale d’une chaîne ${\displaystyle r_{0}=L{\sqrt {N}}}$ est déterminée statistiquement, ainsi que sa longueur maximale ${\displaystyle r_{0}=LN}$. L’expression de la densité d’énergie d’une chaîne isolée est formulée comme suit :

${\displaystyle W={nkT \over 2}{\biggl (}{\lambda \over {\sqrt {N}}}\beta +ln{\biggl (}{\beta \over sinh(\beta )}{\biggr )}{\biggr )}}$

où ${\displaystyle \beta =L^{-1}{\biggl (}{\lambda \over {\sqrt {N}}}{\biggr )}}$ , ${\displaystyle \lambda ={r \over r_{0}}}$ et ${\displaystyle L^{-1}}$ désigne la bijection réciproque de la fonction de Langevin. Cette fonction de Langevin inverse permet de reproduire le durcissement lors des grandes déformations.

De manière générale, tous les modèles statistiques sont basés sur cette théorique statistique non-gaussienne.

Le plus célèbre des modèles statistiques est le modèle d'Arruda-Boyce[7]. Ellen M. Arruda et Mary C. Boyce ont développé le modèle dit « à huit chaînes » en considérant un élément cubique dont les demi-diagonales définissent les huit directions privilégiées de déformation. Le solide complet étant composé d'une multitude d'éléments cubiques. Du fait de la symétrie du modèle par rapport aux trois directions principales du tenseur de déformation, les huit chaînes se déforment toutes de la même quantité ${\displaystyle \lambda _{ch}={\sqrt {I_{1}/3}}}$:

${\displaystyle W={nkT \over 3}{\sqrt {N}}{\biggl (}\lambda _{ch}\beta _{ch}+{\sqrt {N}}ln{\biggl (}{\beta _{ch} \over sinh(\beta _{ch})}{\biggr )}{\biggr )}}$

avec ${\displaystyle \beta _{ch}=L^{-1}{\biggl (}{\lambda _{ch} \over {\sqrt {N}}}{\biggr )}}$.

En 2003, Cornelius O. Horgan, chercheur au département de Génie Civil de l'Université de Virginie (USA), et Giuseppe Saccomandi, chercheur au département d'Ingénierie de l'Innovation à l'Université de Lecce en Italie, ont prouvé[8] que le modèle de Gent, originellement phénoménologique, est analogue au modèle d'Arruda-Boyce à huit chaînes. Ainsi, le modèle de Gent est relié à la microstructure du matériau selon les relations suivantes :

${\displaystyle \mu =nkT}$

${\displaystyle J_{m}=3(N-1)}$.

avec ${\displaystyle \mu }$ le module d'élasticité du modèle de Gent, ${\displaystyle J_{m}}$ un scalaire ayant le rôle de limite d'extensibilité, ${\displaystyle n}$ la densité de chaînes et ${\displaystyle N}$ le nombre moyen de monomères par chaîne.