Fonction de Langevin

La fonction de Langevin apparaît dans la description du paramagnétisme d'un matériau soumis à un champ magnétique uniforme B, ainsi que celle de systèmes formellement apparentés comme un polymère librement joint soumis à une force de traction constante.

Le matériau est décrit comme une assemblée de dipôles magnétiques classiques indépendants, ayant chacun un moment magnétique m dont la direction est libre mais le module, µ, est fixe. L'énergie de chaque dipôle est alors U = −m⋅B.

On se place à température fixée (ensemble canonique). Dans ce cas, l'aimantation du matériau vaut M = n⟨m⟩ où n est la densité de moments magnétiques et la valeur moyenne ⟨m⟩ de ces moments est donnée par la loi de Boltzmann :

${\displaystyle \langle \mathbf {m} \rangle ={\frac {\int \mathbf {m} e^{\frac {\mathbf {m} \cdot \mathbf {B} }{k_{B}T}}d\Omega }{\int e^{\frac {\mathbf {m} \cdot \mathbf {B} }{k_{B}T}}d\Omega }}}$

où k _B est la constante de Boltzmann, T  la température, dΩ l'élément d'angle solide et où l'intégration se fait sur toutes les orientations possibles pour m.

À champ non nul, lorsque la température tend vers zéro on a ⟨M⟩ ≈ nµ : l'aimantation sature (les spins sont gelés dans l'état fondamental). Lorsqu'on se place dans la limite des hautes températures ⟨M⟩ ≈ 0, l'énergie thermique est très supérieure à l'énergie magnétique (régime entropique : les spins ne voient plus le champ magnétique).

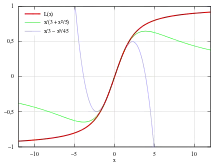
Pour x ≪ 1, la fonction de Langevin peut se développer en série de Taylor :

${\displaystyle L(x)={\tfrac {1}{3}}x-{\tfrac {1}{45}}x^{3}+{\tfrac {2}{945}}x^{5}-{\tfrac {1}{4\;725}}x^{7}+{\tfrac {2}{93\;555}}x^{9}+\cdots }$

ou en fraction continue généralisée :

${\displaystyle L(x)={\frac {x}{3+{\tfrac {x^{2}}{5+{\tfrac {x^{2}}{7+{\tfrac {x^{2}}{9+\cdots }}}}}}}}}$

Dans le régime des hautes températures (kT ≫ µB), on peut garder le seul premier terme de ces développements (L(x) ≈ x/3), ce qui conduit à la loi de Curie :

${\displaystyle \langle M\rangle ={\dfrac {n\mu ^{2}B}{3k_{B}T}}=\chi B}$

avec ${\displaystyle \chi \propto {\dfrac {1}{T}}}$ la susceptibilité magnétique.

La fonction de Langevin vérifie aussi la relation suivante, qui peut se déduire d'un analogue pour la fonction cotangente :

${\displaystyle \forall x\in \mathbb {R} ^{*}\quad L(x)=\displaystyle \sum _{n=1}^{+\infty }{\dfrac {2x}{x^{2}+n^{2}\pi ^{2}}}.}$

• Fonction de Brillouin : analogue de la fonction de Langevin pour des moments magnétiques quantiques.