Gravitoélectromagnétisme
Le gravitoélectromagnétisme, aussi nommé GEM, est une analogie entre les équations de l'électromagnétisme et celles de la gravitation, plus précisément entre les équations de Maxwell et une approximation, valide selon certaines conditions, des équations d'Einstein pour la relativité générale. Le gravitomagnétisme, quant à lui, est un terme largement utilisé pour décrire une analogie entre l'effet cinétique de la gravité et l'effet magnétique engendré par une charge électrique en mouvement.
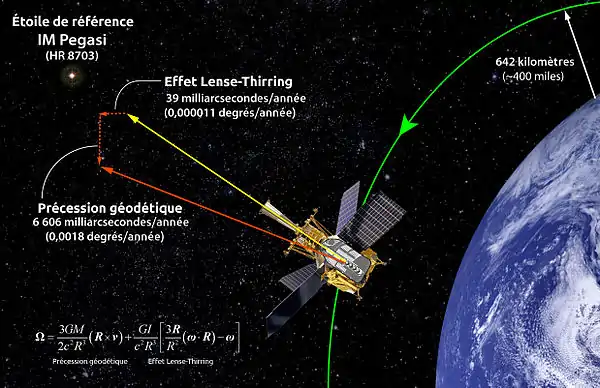
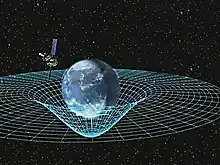
Le GEM intervient dans la description d'effets tels ceux de Lense-Thirring et géodétique. Les premières validations expérimentales de cette théorie ont été effectuées par la sonde Gravity Probe B.
Les bases du GEM ont été publiées comme un complément des lois de Newton par Oliver Heaviside en 1893[1].
Théorie
Selon la relativité générale, le champ gravitationnel produit par un corps en rotation peut, dans certains cas, suivre des équations ayant la même forme que les équations de l'électromagnétisme classique. Dans une situation où le champ gravitationnel est plutôt faible, on peut donc obtenir des équations provenant de la gravitation similaires aux équations de Maxwell.
| Équations du GEM | Équations de Maxwell |
|---|---|
où :
- est le champ gravitationnel (en m⋅s−2) ;
- est le champ électrique ;
- est le champ gravitoélectromagnétique (en s−1) ;
- est le champ magnétique ;
- est la densité en (kg⋅m−3) ;
- est la densité de charge ;
- est le flux de masse (en kg⋅m−2⋅s−1) ;
- , où est la vitesse du flux de masse générant le champ gravitoélectromagnétique ;
- est la densité de courant électrique ;
- est la constante gravitationnelle (en m3⋅kg−1⋅s−2) ;
- est la permittivité du vide ;
- est la vitesse de propagation de la gravité, laquelle est égale à la vitesse de la lumière selon la relativité générale) (en m⋅s−1).
Le GEM est une reformulation approximative de la gravitation présentant un champ apparent différent de celui d'un corps bougeant librement, tel que décrit par la relativité générale dans la limite des champs faibles. Ce champ apparent peut être décrit par deux composantes qui agissent de manière semblable aux champs électrique et magnétique. Par analogie, ils sont appelés respectivement la « gravitoélectricité » et le « gravitomagnétisme » car ils se forment de la même manière autour d'une masse que les champs électromagnétiques autour d'une charge électrique en mouvement.
La principale conséquence du champ gravitomagnétique est qu'un objet se déplaçant près d'un objet massif en rotation aura une accélération qui n'est pas prédite par le seul champ gravitationnel newtonien (gravitoélectrique). Une autre est l'effet Lense-Thirring.
En utilisant le GEM, Roger Penrose a émis l'idée que l'effet Lense-Thirring puisse extraire de l'énergie d'un trou noir en rotation[4], ce qui a été validé par la suite par Reva Key Williams[5] - [6]. Son modèle montre comment l'effet Lense-Thirring peut expliquer en partie la grande énergie et luminosité émises par les quasars et les galaxies actives, les jets bipolaires et les jets asymétriques (cf. #Observations)[7] - [8].



Observations
Des validations indirectes des effets gravitomagnétiques ont été faites à partir de l'analyse de jets relatifs.
Les gyroscopes de la sonde Gravity Probe B ont permis d'observer certains effets décrits par le GEM. Ces derniers ont détecté un déplacement de 39 milliarcsecondes dans un sens et de 6 606 milliarcsecondes dans l'autre[10].
L'Apache Point Observatory Lunar Laser-ranging Operation planifie également d'étudier certains effets du gravitoélectromagnétisme.
Précession géodétique
La précession géodétique est le déplacement graduel de l'axe de rotation du moment cinétique d'un objet suivant une trajectoire en accélération. Cette accélération peut être causée autant par des forces gravitationnelles que d'autres forces qui ne sont pas gravitationnelles[11].
Notes et références
- (en) O. Heaviside, « A gravitational and electromagnetic analogy », The Electrician, vol. 31, , p. 81–82 (lire en ligne)
- (en) B. Mashhoon, F. Gronwald, H. I. M. Lichtenegger, « Gravitomagnetism and the Clock Effect », Lect.Notes Phys., vol. 562, , p. 83–108 (Bibcode 2001LNP...562...83M, arXiv gr-qc/9912027)
- (en) S. J. Clark, R. W. Tucker, « Gauge symmetry and gravito-electromagnetism », Classical and Quantum Gravity, vol. 17, no 19, , p. 4125–4157 (DOI 10.1088/0264-9381/17/19/311, Bibcode 2000CQGra..17.4125C, arXiv gr-qc/0003115)
- (en) Roger Penrose, « Gravitational collapse: The role of general relativity », Rivista de Nuovo Cimento, vol. Numero Speciale 1, , p. 252–276 (Bibcode 1969NCimR...1..252P)
- (en) R. K. Williams, « Extracting x rays, Ύ rays, and relativistic e−e+ pairs from supermassive Kerr black holes using the Penrose mechanism », Physical Review, vol. 51, no 10, , p. 5387–5427 (DOI 10.1103/PhysRevD.51.5387, Bibcode 1995PhRvD..51.5387W)
- (en) R. K. Williams, « Collimated energy–momentum extraction from rotating black holes in quasars and microquasars using the Penrose mechanism », AIP Conference Proceedings, vol. 586, , p. 448–453 (arXiv astro-ph/0111161)
- (en) R. K. Williams, « Collimated escaping vortical polar e−e+ jets intrinsically produced by rotating black holes and Penrose processes », The Astrophysical Journal, vol. 611, no 2, , p. 952–963 (DOI 10.1086/422304, Bibcode 2004ApJ...611..952W, arXiv astro-ph/0404135)
- (en) R. K. Williams, « Gravitomagnetic field and Penrose scattering processes », Annals of the New York Academy of Sciences, vol. 1045, , p. 232–245
- (en) I. Ciufolini et J.A. Wheeler, Gravitation and Inertia, Princeton Physics Series, , 498 p. (ISBN 0-691-03323-4, présentation en ligne)
- (en) Marshall Space Flight Center, « Gravity Probe B - Testing Einstein Universe », sur http://www.nasa.gov,
- (en) C. W. F. Everitt, B. W. Parkinson, « Gravity Probe B Science Results—NASA Final Report »,
Voir aussi
Articles connexes
Liens externes
- (en) [vidéo] Gravity Probe B Video File Part 1/2 sur YouTube
- (en) [vidéo] Gravity Probe B Video File Part 2/2 sur YouTube
- (en)NASA's Gravity Probe B Confirms Two Einstein Space-Time Theories sur le site de la NASA

























