Graphe croix
Le graphe croix est, en théorie des graphes, un graphe possédant 6 sommets et 5 arêtes.
| Graphe croix | |
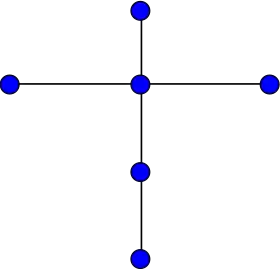 Représentation du graphe croix. | |
| Nombre de sommets | 6 |
|---|---|
| Nombre d'arêtes | 5 |
| Distribution des degrés | 1 (4 sommets) 2 (1 sommet) 4 (1 sommet) |
| Rayon | 2 |
| Diamètre | 3 |
| Maille | ∞ |
| Automorphismes | 6 |
| Nombre chromatique | 2 |
| Indice chromatique | 4 |
| Propriétés | Biparti Planaire Distance-unité Arbre |
Le nom de graphe croix est employé au sein de la classification de l'ISGCI (Information System on Graph Classes and their Inclusions)[1].
Propriétés
Propriétés générales
Le diamètre du graphe croix, l'excentricité maximale de ses sommets, est 3, son rayon, l'excentricité minimale de ses sommets, est 2. Il ne possède aucun cycle, sa maille est donc infinie.
Il s'agit d'un graphe acyclique et connexe, c'est-à-dire d'un arbre. Il est donc 1-sommet-connexe et d'un 1-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il suffit de le priver d'un sommet ou d'une arête.
Toujours parce que le graphe croix est un arbre, il est possible de le tracer sur un plan sans qu'aucune de ses arêtes se croisent. Il est donc planaire. Il est également un graphe distance-unité : il peut s'obtenir à partir d'une collection de points du plan euclidien en reliant par une arête toutes les paires de points étant à une distance de 1.
Coloration
Le nombre chromatique du graphe croix est 2. C'est-à-dire qu'il est possible de le colorer avec 2 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.
L'indice chromatique du graphe croix est 4. Il existe donc une 4-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Il est possible de compter les colorations distinctes du graphe croix. Cela donne une fonction dépendant du nombre de couleurs autorisé. C'est une fonction polynomiale et le polynôme qui lui est associé est qualifiée de polynôme chromatique. Ce polynôme de degré 6 admet pour racines tous les entiers positifs ou nuls strictement inférieurs à 2. Il est égal à : .
Propriétés algébriques
Le groupe d'automorphismes du graphe croix est un groupe d'ordre 6 isomorphe au groupe symétrique S3. Les automorphismes correspondent à toutes les permutations possibles des trois sommets de degré 1 qui sont reliés à l'unique sommet de degré 4.
Le polynôme caractéristique de la matrice d'adjacence du graphe croix est : . Le graphe croix est déterminé de façon unique par son spectre de graphe, l'ensemble des valeurs propres de sa matrice d'adjacence.
Voir aussi
Liens internes
Liens externes
- (en) Eric W. Weisstein, Cross Graph (MathWorld)
Références
- (en) ISGCI (Information System on Graph Classes and their Inclusions), List of small graphs.

