Géométrie dans l'Égypte antique
Dans les mathématiques dans l'Égypte antique, les problèmes de géométrie, présents notamment dans le Papyrus Rhind, concernent l'évaluation de quantités numériques, en particulier le calcul de longueurs, d'aires et de volumes.
Mais, au regard des prouesses techniques et architecturales réalisées très tôt dans leur histoire, il apparait que la géométrie fut sans doute leur domaine de prédilection et cette science associée à l'architecture, fit la grande réputation des Égyptiens. C'est l'une des raisons pour lesquelles leur pays accueillit en pèlerinage les savants de la Grèce antique.
Les Égyptiens réussirent ainsi à calculer l'aire d'un disque en élevant au carré les 8/9 de son diamètre, ce qui revient à une approximation de pi égale à 3,1605. Ils pouvaient calculer les volumes de pyramides et de cylindres et l'aire d'une sphère. Certains problèmes figurant sur les papyrus mathématiques du Moyen Empire permettent de calculer des longueurs associées à des racines d'entiers variées.
Le triangle
.png.webp)
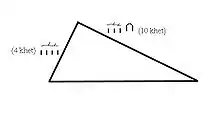
Le calcul de l'aire de cette figure est étudié dans les problèmes R51 du papyrus Rhind, M4, M7 et M17 du papyrus de Moscou et datant tous du Moyen Empire. Le problème R51 constitue, dans l'histoire mondiale des mathématiques, le premier témoignage écrit traitant du calcul de l'aire d'un triangle.
- Énoncé du problème R51 du papyrus Rhind[1]
« Exemple de calcul d'un triangle de terre. Si quelqu'un te dit : « Un triangle de dix khet sur son mryt et de quatre khet sur sa base. Quelle est sa superficie ? ». Calcule la moitié de quatre qui est deux pour en faire un rectangle. Tu fais en sorte de multiplier dix par deux. Ceci est sa superficie. »
Le terme mryt signifie probablement hauteur ou côté, mais la formule utilisée pour le calcul de l'aire fait pencher l'interprétation en faveur de la première solution[2]. Le scribe prenait la moitié de la base du triangle et calculait l'aire du rectangle formé par ce côté et la hauteur, soit
équivalente à la formule générale utilisée de nos jours :
Le triangle 3-4-5
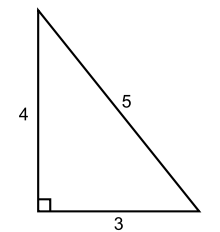
Un triangle dont les côtés sont en proportion 3-4-5 est rectangle, l'angle droit étant défini par les côtés 3 et 4. Cette propriété se démontre par la réciproque du théorème de Pythagore, du fait que 32 + 42 = 52 (car 9 + 16 = 25). Un tel triangle est parfois appelé « triangle égyptien », en référence à Plutarque et à son traité Sur Isis et Osiris où il donne une interprétation ésotérique du triangle 3-4-5, le liant à Isis, Osiris et Horus[3]. Plutarque écrit à la fin du Ier siècle ou au début du suivant, et on ne peut rien en déduire à propos de l'Égypte antique[4].
Le triangle rectangle 3-4-5 est très anciennement connu : le triplet pythagoricien 3-4-5 est mentionné sur des tablettes babyloniennes, mais en ce qui concerne l'Égypte antique, les choses sont beaucoup moins claires. Quatre des sections du papyrus Rhind : R57, R58, R59a et R59b, ont pour objet des calculs relatifs à la pente d'une pyramide[5], et cette pente est de 4/3 (voir papyrus Rhind), c'est-à-dire que le triangle correspondant, dont les côtés sont la demi-base de la pyramide, sa hauteur, et la ligne de plus grande pente d'une face, est proportionnel au triangle 3-4-5. Cependant aucun de ces problèmes ne donne la mesure du troisième côté, ni même ne parle de triangle[6].
Il est possible que les architectes égyptiens, assistés de tendeurs de corde, aient tracé parfois leurs angles droits au moyen du triangle 3-4-5, mais il n'existe pas de traces écrites. La méthode ne pouvait pas fonctionner pour les édifices de grande dimension comme les pyramides, vu la précision de la méthode et ce que l'on sait des cordes utilisées à l'époque et de leur élasticité[7].
La pyramide de Khéphren a pu être construite en respectant le triangle directeur des quatre exemples du papyrus Rhind : la ligne de plus grande pente d'une face étant comme 5, la verticale du sommet à la base est comme 4 et la demi-base qui termine le triangle rectangle est comme 3, ce qui correspond à un angle théorique de 53°07'48" de la ligne de plus grande pente avec l'horizontale. L'angle mesuré par Petrie (53°10', voir pyramide de Khéphren) est très proche de cette valeur. Le carré de la base, de 215,16 m de côté, est exact à 8 cm près, les côtés sont parallèles à 1' près, les faces sont orientées avec les points cardinaux à 5' près. La hauteur, évaluée à 143,87 m, correspond pour le tétraèdre à une pente de 53°13'[8].
Calcul d'une pente
Les problèmes R56, R57, R58 et R59 du papyrus Rhind détaillent la méthode de calcul de la pente d'une pyramide. Cette pente est désignée en ancien égyptien par le terme seqed. Elle est le résultat de la demi-base divisée par la hauteur.
- Énoncé du problème R56 du papyrus Rhind[9]
« Une pyramide dont le côté est de 360 (coudées) et dont la hauteur est 250 (coudées). Fais en sorte de connaitre sa pente. Prends la moitié de 360. Le résultat est 180. Multiplie 250 de sorte à trouver 180. Cela fait 1/2 1/5 1/50 d'une coudée. Une coudée vaut 7 palmes. Multiplie 7 comme il suit : »
| 1 | 7 | |
| 1/2 | 3 1/2 | |
| 1/5 | 1 1/3 1/15 | |
| 1/50 | 1/10 1/25 | |
« La pente est de 5 1/25 palmes. »
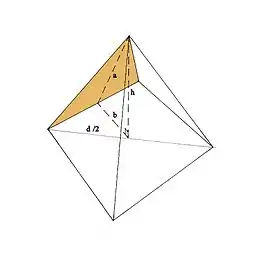
Cette solution représente pour le mathématicien moderne le produit par sept de la cotangente de l'angle formé par la demi-base et l'apothème de la pyramide (l'angle formé par b et a sur la figure ci-contre). Les Égyptiens l'exprimèrent en coudées, puis finalement en palmes (une coudée valant sept palmes). Le seqed ne représentait donc pas à proprement parler une pente, mais plutôt la mesure du côté horizontal du triangle proportionnel dont la hauteur vaut une coudée, côté exprimé ensuite en palmes. Par conséquent, la formule suivante permettait d'obtenir le seqed de la pyramide : .
Le seqed correspond également à la différence de longueur des côtés inférieur et supérieur d'une pierre qui épouse la pente de la pyramide. Il permettait donc d'en déterminer la coupe.
Le trapèze ou triangle tronqué
L'aire d'un trapèze est parfaitement calculé dans le problème R52 du papyrus Rhind[10] :
« Si on te dit : « Quelle est l'aire d'un triangle tronqué d'un terrain de vingt khet en sa hauteur, de six khet en sa base et de quatre khet en sa ligne tronquée ? ». Ajoutes sa base à sa ligne tronquée. Cela fait dix. Prends la moitié de dix, cinq, de sorte à obtenir un rectangle. Fais vingt fois cinq. Cela fait cent. Ceci est sa surface. Calcule comme il suit : »
| 1 | 1000 | |
| 1/2 | 500 | |
| ✔ | 1 | 2000 |
| 2 | 4000 | |
| ✔ | 4 | 8000 |
| 10000 (100 setjat) | ||
Méthode équivalente à l'application de la formule .
Le rectangle
Le papyrus de Moscou présente un problème illustrant la parfaite connaissance du calcul de l'aire d'un rectangle :
- Énoncé du problème M6 du papyrus de Moscou[11]
« Exemple de calcul d'un rectangle. Si quelqu'un te dit : Un rectangle de 12 setjat, d'une largeur de 1/2 1/4 sa longueur. Calcule 1/2 1/4 pour avoir 1. Le résultat est 1 1/3. Prends les 12 setjat fois 1 1/3. Le résultat est 16. Calcule sa racine carrée. Le résultat est 4 pour sa longueur. 1/2 1/4 de ceci est 3 pour la largeur. »
- Explication
Ce problème consiste à déterminer la longueur d'un rectangle, le rapport largeur/longueur et l'aire étant fixés.
| Problème posé par le scribe | Transcription du problème en langage algébrique moderne |
| Un rectangle de 12 setjat. | Soit un rectangle dont l'aire est de 12 Setjat (que l'on désigne par B). B = 12. |
| d'une largeur de 1/2 1/4 sa longueur. | Le rapport de la largeur sur la longueur de ce rectangle est de 1/2 + 1/4. soit L cette longueur. la largeur vaut l=L*(1/2+1/4) |
| Calcule 1/2 1/4 pour avoir 1. | Choisis une largeur de 1 et calcule la longueur en faisant l'inverse de 1/2 + 1/4. |
| Le résultat est 1 1/3. | Le résultat est 1 + 1/3, rapport de la longueur sur la largeur. |
| Prends les 12 setjat fois 1 1/3 | Calcule B*(1+1/3) soit L*[L*(1/2+1/4)]*(1+1/3)=L² ce qui revient à transformer le rectangle en carré de côté L. |
| Le résultat est 16. | L² = 16. |
| Calcule sa racine carrée. | Calcule L. |
| Le résultat est 4 pour sa longueur. | L = 4. La longueur du rectangle de 12 setjat est donc 4. |
| 1/2 1/4 de ceci est 3 pour la largeur. | La largeur du rectangle de 12 setjat vaut 4 * (1/2+1/4), soit l=3. |
Le cercle et l'ellipse
Le calcul de l'aire d'un disque représente sans doute l'un des progrès les plus significatifs effectué en mathématiques par les anciens égyptiens. Il est également l'un des exercices qui a fait couler le plus d'encre, le nombre pi et la quadrature du cercle semblant intimement liés au problème. Le calcul de l'aire est ainsi traité dans les problèmes R41, R42, R43, R48 et R50 du papyrus Rhind et enfin le problème M10 du papyrus de Moscou.
- Énoncé du problème R50 du papyrus Rhind[12]
« Exemple de calcul d'un champ rond de neuf khet. De combien est la surface du champ ? Soustrais son neuvième qui est un. Il reste huit. Multiplie huit par huit. Cela fait soixante-quatre. Ceci est la surface du champ, à savoir soixante-quatre setjat. Fais comme suit : »
| 1 | 9 | |
| ✔ | 1/9 | 1 |
« Soustrais-le, il reste 8 »
| 1 | 8 | |
| 2 | 16 | |
| 4 | 32 | |
| ✔ | 8 | 64 |
« La surface du champ est soixante-quatre setjat. »
La formule appliquée par la scribe est donc clairement : , d étant le diamètre du disque. L'énoncé évoque un champ rond de neuf khet, étant sous-entendu que neuf khet est le diamètre.
Cette formule est équivalente à celle-ci : . La formule moderne du calcul de l'aire d'un disque étant ou , la plupart des auteurs attribuent aux anciens Égyptiens l'approximation de la valeur à 256/81 soit 3,1605, valeur remarquable pour l'époque[13]. Cependant, le problème R50 exposé ci-dessus ne prouve pas que les Égyptiens aient eu conscience de l'existence de cette constante. La seule certitude est qu'ils pouvaient calculer l'aire d'un disque à partir de son diamètre, et d'en donner une valeur approchée avec une grande précision en l'assimilant à un carré. La méthode employée pourrait bien trouver une explication dans une esquisse géométrique du problème R48 du papyrus Rhind[14].
- Opérations du problème R48 du papyrus Rhind
| 1 | 8 setjat | |
| 2 | 16 setjat | |
| 4 | 32 setjat | |
| ✔ | 8 | 64 setjat |
et
| ✔ | 1 | 9 setjat |
| 2 | 18 setjat | |
| 4 | 36 setjat | |
| ✔ | 8 | 72 setjat |
| 81 | ||
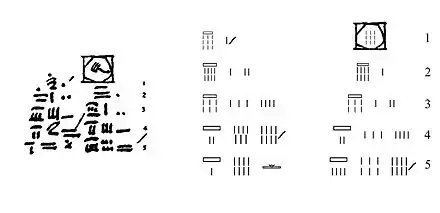
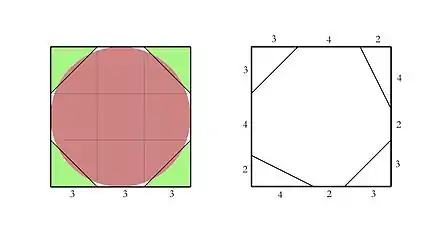
Le problème ne contient aucun énoncé, ce qui rend son interprétation délicate. Néanmoins, son intérêt réside dans l'esquisse accompagnant les opérations mathématiques décrites ci-dessus. Celle-ci représente un cercle maladroitement dessiné (ou bien une figure octogonale) inscrit dans un carré. À l'évidence, les calculs sont relatifs à l'aire du disque de diamètre neuf, comparable à celui du problème R50.
La première hypothèse concernant ce dessin est que le scribe considère le disque dont il cherche l'aire comme équivalent à un octogone. Ce dernier est ainsi inscrit dans un carré dont les côtés sont égaux au diamètre du disque. L'octogone ayant une aire de 9² - 2 * 3² = 63, la surface du disque est alors approximée à 64[15].
La deuxième hypothèse, avancée par Michel Guillemot, reproduit plus fidèlement le dessin et considère que la surface du disque est équivalente à un octogone irrégulier dont l'aire est exactement de 9² - (3² + 2*4) = 64 (voir figure ci-dessous). Cet auteur est allé plus loin en émettant l'hypothèse que le scribe pouvait reconstituer un carré de côté 8 en décomposant cet octogone, ce qui revient à avancer que l'idée de quadrature du cercle était déjà présente à leur esprit[16]. Cette dernière hypothèse a toutefois le mérite de donner une explication satisfaisante à la formule utilisée au problème R50, qui revient à avancer l'égalité entre l'aire d'un disque et l'aire d'un carré dont les côtés sont égaux au 8/9e du diamètre du disque.
Cette recherche géométrique pourrait trouver un équivalent dans une autre esquisse, découverte sur un mur du temple de Louxor par Ludwig Borchardt. Il s'agit d'une ellipse construite à l'aide d'un rectangle, les aires des deux figures n'étant différentes que de 1 %[17].
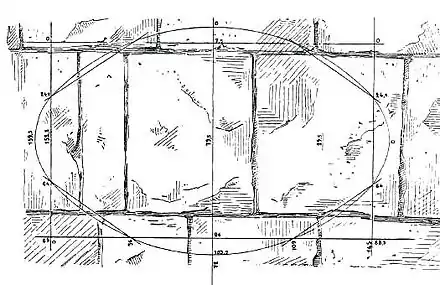
.
La demi-sphère

L'énoncé M10 du papyrus de Moscou fut étudié maintes fois mais les auteurs ne s'accordent toujours pas sur l'interprétation du problème. Les tenants de l'étude de la surface d'un demi-cercle s'opposent à ceux de l'étude d'une demi-sphère. Il semble bien, au vu de l'énoncé et en dépit des nombreuses questions que cela engendre, que cette dernière proposition soit la plus acceptable.
- Énoncé du problème M10 du papyrus de Moscou
« Exemple de calcul d'un nbt. Si on te dit : « Un nbt dont la base est 4 1/2 entre limites. Peux-tu me faire connaitre sa surface ? ». Tu feras en sorte de calculer 1/9 de 9. À cause de cela, le nbt est la moitié d'un objet rond, il adviendra 1. Tu feras en sorte de calculer le reste à 8. Tu feras en sorte de calculer 1/9 de 8. Il adviendra 2/3 1/6 1/18. Tu feras en sorte de calculer le reste de ce 8 par rapport à ce 2/3 1/6 1/18. Il advient 7 1/9. Alors, tu feras en sorte de calculer 7 1/9, 4 1/2 fois. Il adviendra 32. Voici sa surface. Tu as trouvé parfaitement. »
Le terme nbt est traduit par corbeille. L'égyptien aboutit donc à un calcul donnant 32 comme résultat. Sylvia Couchoud a remarqué que la formule de la surface d'une demi-sphère, étant remplacé par le rapport égyptien 256/81, donne exactement le même résultat[18].
Calcul d'un volume
Autant l'arpentage nécessitait de solides connaissances quant aux calculs des aires, autant la vie domestique et la construction des grands édifices nécessitaient de savoir calculer des volumes, tels que ceux des greniers à blé ou des grandes constructions funéraires.
Volume d'un cube
Comme le montre le problème R44 du papyrus Rhind, la formule du volume d'un solide de forme cubique était connue des anciens Égyptiens : V = l * L * H où l, L et H sont respectivement la longueur, la largeur et la hauteur.
- Énoncé du problème R44 du papyrus Rhind[19]
« Exemple de calcul d'un grenier rectangulaire. Sa longueur est 10, sa largeur est 10 et sa hauteur est 10. Quel montant de grain cela fait-il ? Multiplie 10 par 10. Cela fait 100. Multiplie 100 par 10. Cela fait 1000. Prends la moitié de 1000, soit 500. Cela fait 1500. C'est sa quantité en khar. Prends 1/20 de 1500. Cela fait 75, sa quantité en quadruple-heqat, soit 7500 heqat de grain. »
Volume d'un cylindre (application aux greniers à blé)
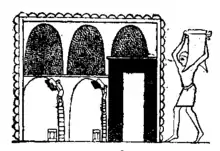
Les calculs de volume d'un cylindre interviennent dans les études du contenu des grenier à blé dont la base est ronde. Les représentations égyptiennes de ce type de grenier sont fréquentes (voir ci-contre). Le sommet est de forme ovoïde mais celui-ci n'est jamais pris en compte dans les calculs. L'introduction du grain se faisant par une trappe située au sommet, le tas de grain ne devait jamais dépasser la limite à partir de laquelle le diamètre du grenier diminuait.
Il existe deux types de calcul d'un tel volume. L'exemple suivant présente le premier type, fondé sur le calcul de l'aire d'un disque.
- Énoncé du problème R41 du papyrus Rhind[20]
« Exemple de calcul d'un grenier rond dont le diamètre est 9 et la hauteur, 10. Extrait 1/9 de 9, soit 1. Le reste est 8. Multiplie 8 par 8. Cela fait 64. Multiplie 64 par 10. Cela fait 640 coudées (Sous-entendu coudées cubiques). Ajoute la moitié de cela à cela. Cela fait 960: le contenu en khar. Prends 1/20 de 960, soit 48. C'est ce que cela donne en quadruple-heqat de grains, 48 heqat. »
Méthode de calcul :
| 1 | 8 | |
| 2 | 16 | |
| 4 | 32 | |
| ✔ | 8 | 64 |
et
| 1 | 64 | |
| ✔ | 10 | 640 |
| ✔ | 1/2 | 320 |
| 960 | ||
| ✔ | 1/10 | 96 |
| ✔ | 1/20 | 48 |
La formule algébrique équivalente serait donc , avec d le diamètre du disque et h, la hauteur du cylindre.
Le papyrus Kahun quant à lui, présente un calcul faisant intervenir une seconde méthode :
- Calcul du problème K4 du papyrus Kahun
| ✔ | 1 | 12 |
| 2/3 | 8 | |
| ✔ | 1/3 | 4 |
| 16 | ||
et
| ✔ | 1 | 16 |
| ✔ | 10 | 160 |
| ✔ | 5 | 80 |
| 256 | ||
et
| ✔ | 1 | 256 |
| 2 | 512 | |
| ✔ | 4 | 1024 |
| ✔ | 1/3 | 85 1/3 |
| 1365 1/3 | ||
Ce calcul, répondant au problème du calcul d'un cylindre dont l'énoncé manque, peut être traduit en langage algébrique moderne. L'énoncé devait demander au scribe de calculer le volume en khar d'un grenier rond de 12 coudées de diamètre et de 8 coudées de hauteur.
Nous traduirions le raisonnement du scribe par l'application de cette formule : , formule strictement équivalente à celle énoncée plus haut reposant sur le calcul de l'aire d'un disque[21].

Volume d'une pyramide tronquée
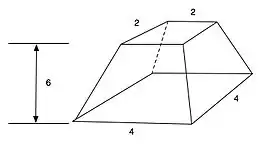
Le problème M14 du papyrus de Moscou est remarquable en ce sens qu'il dévoile l'extraordinaire capacité des anciens Égyptiens à inventer et utiliser des méthodes de calcul complexes et d'une parfaite justesse.
- Énoncé du problème M14 du papyrus de Moscou
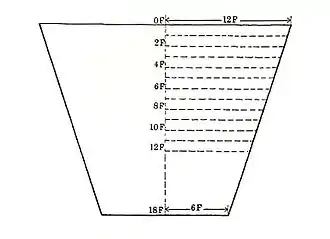
« Méthode de calcul d'une pyramide tronquée. Si on te dit : Une pyramide de 6 pour la hauteur par 4 sur la base, par 2 sur le sommet. Calcule le carré de 4. Le résultat est 16. Prends le double de 4. Le résultat est 8. Prends le carré de 2. Le résultat est 4. Tu dois additionner le 16, le 8 et le 4. Le résultat est 28. Prends 1/3 de 6. Il vient 2. Prends 2 fois 28. Il vient 56. Le résultat est 56. Tu trouveras cela correct. »
Cet énoncé décrit le calcul suivant :
que l'on pourrait traduire très exactement par :
formule générale exacte d'une pyramide tronquée.
Le moyen mis en œuvre par les Égyptiens pour déterminer une méthode aussi complexe nous est inconnu. Les Babyloniens ne sont parvenus qu'à une approche approximative du résultat pouvant être associée à la formule suivante :
- [22].
Volume d'un tronc de cône
Un papyrus d'époque tardive, mais découvert en Égypte à Oxyrhynque traite du volume d'un tronc de cône identifié à une clepsydre. La description de cet instrument rappelle de très près la clepsydre de Karnak et démontre que les anciens Égyptiens furent très tôt capables de calculer de tels volumes.
Notes et références
- A. Buffum Chace, Rhind papyrus, pl. 73.
- M. Clagett, Ancient Egyptian Science, p. 70.
- Rossi 2007, p. 64.
- Rossi 2007, p. 64-65.
- S. Couchoud, Math. Égyptiennes, p. 79.
- (en) Corinna Rossi, Architecture and Mathematics in Ancient Egypt, Cambridge University Press, (1re éd. 2003), 280 p. (ISBN 978-0-521-69053-9), p. 218.
- Rossi 2007, p. 155.
- Numériquement : atan(2x143,87/215,16) = 53°13' et atan(4/3) = 53°07'48".
- A. Buffum Chace, Rhind Papyrus, pl. 78
- A. Buffum Chace, Rhind Papyrus, pl. 74
- M. Clagett, Ancient Egyptian Science, p. 69.
- A. Buffum Chace, Rhind Papyrus, pl. 72
- S. Couchoud, Math. Égyptiennes, p. 64-65.
- S. Couchoud, Math. Égyptiennes, p. 66.
- K. Vogel, Vorgriechische Mathematik, p. 66.
- M. Guillemot, À propos…, p. 125-146.
- L. Borchardt, Altägyptische Werkzeichnung, pl. VI
- S. Couchoud, Math. Égyptiennes, p. 88-96.
- A. Buffum Chace, Rhind Papyrus,, pl. 66
- A. Buffum Chace, Rhind Papyrus, pl. 63
- M. Clagett, Ancient Egyptian Science, p. 82.
- S.Couchoud, Math. Égyptiennes, p. 86-88.
Sources
- Arnold Buffum Chace, The Rhind Mathematical Papyrus : Free Translation and Commentary with Selected Photographs, Translations, Transliterations and Literal Translations, vol. II, 1927-1929
- Marianne Michel, Les mathématiques de l'Égypte ancienne. Numération, métrologie, arithmétique, géométrie et autres problèmes, Bruxelles, Safran (éditions), , 604 p. (ISBN 978-2-87457-040-7).
- Sylvia Couchoud, Mathématiques Égyptiennes. Recherches sur les connaissances mathématiques de l’Égypte pharaonique, éditions Le Léopard d’Or,
- (en) Marshall Clagett, Ancient Egyptian Science, A Source Book, vol. 3 : Ancient Egyptian Mathematics, American Philosophical Society,
- Kurt Vogel, Vorgriechische Mathematik, vol. I
- Michel Guillemot, « À propos de la géométrie égyptienne des figures », Sciences et Technique en Perspective, vol. 21,
- Ludwig Borchardt, Altägyptische Werkzeichnung,
- Théophile Obenga, La Géométrie égyptienne, contribution de l'Afrique antique à la mathématique mondiale, Chez L'Harmattan,
- Vasily Vasilievich Struve, Mathematischer Papyrus des Stastlichen Musuems der Scönen Künste in Moskau,










![{\displaystyle Volume_{cylindre-en-khar}=[(d-(1/9)*d)^{2}]*h*(3/2)}](https://img.franco.wiki/i/abd82d4c4f48099c4a86fa560cc2f48962d12a2d.svg)
![{\displaystyle Volume_{cylindre-en-khar}=(2/3)*h*[d+(d/3)]^{2}}](https://img.franco.wiki/i/304a0c6ed6c011ec8da6083c7dab806bd05db90f.svg)


