Formule de Clausius-Clapeyron

On intègre la formule impliquant l'entropie de vaporisation (une entropie de changement d'état ne dépend que de la température) avec un point d'ébullition de référence ${\displaystyle \left(P^{\circ },T^{\circ }\right)}$ :

${\displaystyle \int _{P^{\circ }}^{P^{\text{sat}}}\,\mathrm {d} \ln P=\int _{T^{\circ }}^{T}{\Delta _{\text{vap}}S \over R}\,\mathrm {d} \ln T}$

En considérant l'entropie de vaporisation comme constante :

${\displaystyle \ln \left({P^{\text{sat}} \over P^{\circ }}\right)={\Delta _{\text{vap}}S \over R}\,\ln \left({T \over T^{\circ }}\right)}$

on obtient une formule similaire à la formule de Duperray[6] - [7] :

Formule de Duperray : ${\displaystyle {P^{\text{sat}} \over P^{\circ }}=\left({T \over T^{\circ }}\right)^{\Delta _{\text{vap}}S \over R}}$

que l'on peut généraliser à l'aide de deux constantes ${\displaystyle A}$ et ${\displaystyle B}$ déterminées expérimentalement :

Formule de Duperray : ${\displaystyle P^{\text{sat}}=A\,T^{B}}$

Figure 1 - Enthalpies de vaporisation de l'eau, du méthanol, du benzène et de l'acétone en fonction de la température.

On intègre la formule impliquant l'enthalpie de vaporisation (une enthalpie de changement d'état ne dépend que de la température) avec un point d'ébullition de référence ${\displaystyle \left(P^{\circ },T^{\circ }\right)}$ :

${\displaystyle \int _{P^{\circ }}^{P^{\text{sat}}}\,\mathrm {d} \ln P=\int _{T^{\circ }}^{T}{\Delta _{\text{vap}}H \over RT^{2}}\,\mathrm {d} T}$

En supposant que l'enthalpie de vaporisation est de la forme :

${\displaystyle \Delta _{\text{vap}}H=\alpha +\beta T+\gamma T^{2}+\delta T^{\varepsilon }}$

avec ${\displaystyle \varepsilon }$ un paramètre d'ajustement pouvant être un nombre non entier, voire un nombre négatif, les bases de données comme la base DIPPR de l'AIChE[8] donnent une équation d'Antoine étendue à sept constantes[9] :

Équation d'Antoine étendue : ${\displaystyle \ln P^{\text{sat}}=A+{B \over T+C}+D\,\ln T+ET+FT^{G}}$

avec :

${\displaystyle A=\ln P^{\circ }-{B \over T^{\circ }}-D\,\ln T^{\circ }-ET^{\circ }-F{T^{\circ }}^{G}}$

${\displaystyle B=-{\alpha \over R}}$

${\displaystyle D={\beta \over R}}$

${\displaystyle E={\gamma \over R}}$

${\displaystyle F={\delta \over R\cdot \left(\varepsilon -1\right)}}$

${\displaystyle G=\varepsilon -1}$

La constante ${\displaystyle C}$ est introduite à postériori pour ajuster plus précisément la corrélation à des données expérimentales[9] - [10]. Dans la pratique, les sept constantes sont toutes déterminées sur base de données expérimentales, notamment afin d'appliquer cette équation sur toute l'étendue de la courbe d'équilibre liquide-vapeur, du point triple au point critique, malgré les hypothèses simplificatrices prises pour l'établir.

En prenant ${\displaystyle \alpha =\gamma =\delta =0}$ et ${\displaystyle \beta =\Delta _{\text{vap}}S}$ on retrouve la formule de Duperray.

Si l'on considère l'enthalpie de vaporisation comme une constante, ${\displaystyle \Delta _{\text{vap}}H=\alpha }$, on obtient la formule de Rankine[11] :

Formule de Rankine : ${\displaystyle \ln P^{\text{sat}}=A+{B \over T}}$

soit, de façon explicite :

Formule de Rankine : ${\displaystyle \ln \!\left({P^{\text{sat}} \over P^{\circ }}\right)=-{\Delta _{\text{vap}}H \over R}\cdot \left({1 \over T}-{1 \over T^{\circ }}\right)}$

En introduisant une troisième constante ${\displaystyle C}$ on obtient l'équation d'Antoine :

Équation d'Antoine : ${\displaystyle \ln P^{\text{sat}}=A+{B \over T+C}}$

Aux basses températures on peut approximativement considérer que l'enthalpie de vaporisation varie selon une droite de pente négative (voir figure 1), soit ${\displaystyle \Delta _{\text{vap}}H=\alpha +\beta T}$ avec ${\displaystyle \alpha >0}$ et ${\displaystyle \beta <0}$, on obtient la formule de Dupré[6] :

Formule de Dupré : ${\displaystyle \ln P^{\text{sat}}=A+{B \over T}+D\,\ln T}$

L'enthalpie de vaporisation devant avoir une tangente verticale au point critique (voir figure 1), comportement qui ne peut être qu'approché par une forme polynomiale, la formule de Riedel se base sur les paramètres ${\displaystyle \gamma =0}$, ${\displaystyle \delta <0}$ et ${\displaystyle \varepsilon =7}$, soit ${\displaystyle \Delta _{\text{vap}}H=\alpha +\beta T+\delta T^{7}}$, ce qui induit :

Formule de Riedel : ${\displaystyle \ln P^{\text{sat}}=A+{B \over T}+D\,\ln T+FT^{6}}$

Riedel donne des corrélations permettant de déterminer les paramètres ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle D}$ et ${\displaystyle F}$ à partir des coordonnées du point critique, du point d'ébullition standard ou du facteur acentrique du corps pur[12].

Détermination de l'enthalpie de vaporisation (notée L).

La température et la pression d'équilibre associée d'un gaz au contact de son liquide peuvent être mesurées expérimentalement dans un autoclave. On peut ainsi déterminer l'évolution de la pression d'équilibre ou pression de vapeur saturante en fonction de la température. En considérant que l'enthalpie de vaporisation est constante sur l'intervalle de température expérimental, selon la formule de Rankine :

${\displaystyle \ln \!\left({P_{\text{vap}} \over P^{\circ }}\right)=-{\Delta _{\text{vap}}H \over R}\cdot \left({1 \over T}-{1 \over T^{\circ }}\right)}$

${\displaystyle \ln P_{\text{vap}}+{\Delta _{\text{vap}}H \over R}{1 \over T}=\ln P^{\circ }+{\Delta _{\text{vap}}H \over RT^{\circ }}=A={\text{Cste}}}$

d'où :

${\displaystyle \ln P_{\text{vap}}=-{\Delta _{\text{vap}}H \over R}{1 \over T}+A}$

Si l'on trace le graphe ${\displaystyle \ln P_{\text{vap}}=\operatorname {f} \left({1 \over T}\right)}$ on obtient une droite de pente négative, voir figure ci-contre :

${\displaystyle {\text{pente}}=-{\Delta _{\text{vap}}H \over R}}$

La détermination graphique de cette pente permet le calcul de l'enthalpie de vaporisation :

${\displaystyle \Delta _{\text{vap}}H=-{\text{pente}}\cdot R}$

En météorologie, la formule de Clausius-Clapeyron est utilisée couramment dans les diagrammes thermodynamiques comme les téphigrammes, Skew-T et émagrammes pour le calcul des énergies de changement de phase de l'eau atmosphérique (notée ${\displaystyle L}$). Sur un diagramme pression-température (P-T), la ligne séparant les deux phases est la courbe de coexistence ${\displaystyle \mathrm {d} P/\mathrm {d} T}$. Pour la pression de vapeur saturante de l'eau ${\displaystyle e_{s}}$, la formule de Clausius-Clapeyron devient[13] :

${\displaystyle {\mathrm {d} e_{s} \over \mathrm {d} T}={L\,e_{s} \over R\,T^{2}}}$

où ${\displaystyle R}$ est la constante universelle des gaz parfaits.

Une augmentation de température de 1 °C est associée une augmentation globale de l’humidité de l’atmosphère d’environ 7 % conformément à la loi de Clausius-Clapeyron qui régule la quantité d’eau dans l’atmosphère en fonction de la température. Dans ses scénarios RCP, le GIEC estime l’augmentation des précipitations de 1 à 3 % °C⁻¹ pour les RCP 4.5, RCP 6 et RCP 8.5, et 0,5 à 4 % °C⁻¹ pour le RCP 2.6[14].

Diagramme de Cox-Othmer pour divers alcools. Le liquide de référence est l'eau. Pressions en millimètres de mercure (mmHg).

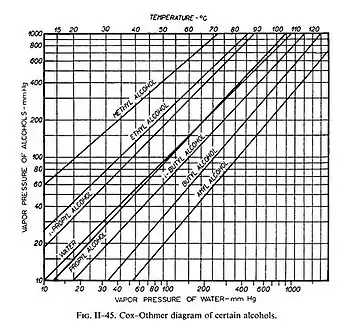
Dans ces deux types de diagramme, le point d'ébullition de divers corps sont tracés en fonction du point d'ébullition d'un corps de référence. Les courbes obtenues sont quasiment des droites. Ces droites sont calculées en intégrant la formule de Clausius-Clapeyron en utilisant l'hypothèse de l'enthalpie de vaporisation constante.

• Jean-Pierre Corriou, Thermodynamique chimique : Définitions et relations fondamentales, vol. J 1025, Techniques de l'ingénieur, coll. « base documentaire Thermodynamique et cinétique chimique, pack Opérations unitaires. Génie de la réaction chimique, univers Procédés chimie - bio - agro », 1984 (lire en ligne), p. 13.
• Jean Vidal, Thermodynamique : application au génie chimique et à l'industrie pétrolière, Paris, Éditions Technip, coll. « Publications de l'Institut français du pétrole. », 1997, 500 p. (ISBN 978-2-7108-0715-5, OCLC 300489419, lire en ligne), p. 38-39.