Espace localement simplement connexe
En mathématiques, un espace localement simplement connexe est un espace topologique qui admet une base d'ouverts simplement connexes[1] - [2]. Tout espace localement simplement connexe est donc localement connexe par arcs et a fortiori localement connexe.
Exemples et contre-exemples
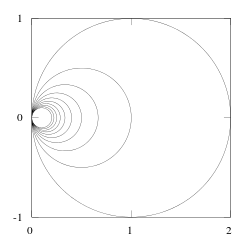
La boucle d'oreille hawaïenne n'est pas localement simplement connexe.
- Le cercle est localement simplement connexe mais pas simplement connexe.
- La boucle d'oreille hawaïenne n'est pas localement simplement connexe ni simplement connexe, puisqu'elle n'est même pas semi-localement simplement connexe (en).
- Le cône de la boucle d'oreille hawaïenne est contractile donc simplement connexe, mais n'est pas localement simplement connexe.
- Toutes les variétés topologiques et tous les CW-complexes sont localement simplement connexes, puisqu'ils sont même localement contractiles.
Notes et références
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Locally simply connected space » (voir la liste des auteurs).
- (en) James R. Munkres, Topology, Prentice Hall, , 2e éd. (ISBN 0-13-181629-2).
- (en) Allen Hatcher, Algebraic Topology, Cambridge University Press, (ISBN 0-521-79540-0, lire en ligne).
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.