Effet Ramsauer-Townsend

Quand un électron se déplace dans un gaz, il est amené à interagir avec les atomes, ce qui provoque sa diffusion. Les collisions sont qualifiées d'inélastiques si elles provoquent l'excitation ou l'ionisation de l'atome et élastiques si ce n'est pas le cas.

La probabilité de diffusion dans un tel système est fonction du nombre d'électrons diffusés, par unité de courant électronique, par unité de longueur du chemin, par unité de pression à 0 °C, par unité d'angle solide. Le nombre de collisions égale le nombre total d'électrons diffusés (élastiquement ou non) pour tous les angles ; la probabilité de collision est le nombre total de collisions, par unité de courant électronique, par unité de longueur du chemin, par unité de pression à 0 °C.

Puisque les atomes des gaz nobles possèdent une première énergie d'ionisation élevée et que les électrons transportent une énergie cinétique relativement faible, il est très peu probable qu'ils provoquent une ionisation ou une excitation de l'atome ; la probabilité d'une diffusion élastique en direction de tous les angles égale environ la probabilité de collision.

En haut, un atome est représenté par un disque jaune, alors que la trajectoire de l'électron est modélisée par la ligne noire. Le graphique (en bas) donne grossièrement la relation entre le courant électronique et la tension pour l'argon. Le courant ne croît pas de façon monotone lorsque la tension augmente, ce que ne peut expliquer la mécanique newtonienne.

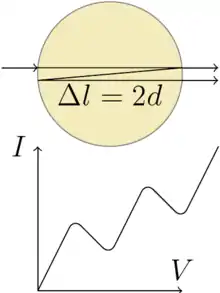
Si quelqu'un tente de prédire la probabilité de collision à l'aide d'un modèle qui s'appuie sur la mécanique newtonienne, en modélisant les atomes et les électrons comme des boules dures, il établit que la probabilité de collision décroît de façon monotone lorsque l'énergie de l'électron s'accroît. Cependant, Ramsauer et Townsend ont observé que, pour des électrons se déplaçant lentement dans l'argon, le krypton ou le xénon, la probabilité de collision entre les électrons et les atomes gazeux atteint une valeur minimale pour les électrons possédant une certaine énergie cinétique. La différence entre le modèle newtonien et l'expérience est appelé l'« effet Ramsauer-Townsend »[1].

Jusqu'à l'introduction de la mécanique quantique, aucune explication satisfaisante n'existait. Cet effet s'explique à l'aide des propriétés ondulatoires des électrons. Un modèle relativement simple de la collision qui fait appel à la mécanique quantique ondulatoire prédit de façon satisfaisante la valeur minimale. David Bohm a conçu une théorie qui modélise l'atome comme puits de potentiel carré fini[2].

Prédire la quantité d'énergie cinétique qui générera la valeur minimale est plutôt difficile puisqu'il faut étudier les particules à l'aide d'un modèle ondulatoire. Ce problème a fait l'objet d'études approfondies, tant expérimentalement que théoriquement, il est donc très bien compris (par exemple, consulter Johnson et Guet 1994).

• (en) J. S. Townsend et V. A. Bailey, « The motion of electrons in gases », Philosophical Magazine, vol. S.6, n^o 42,‎ 1921, p. 873–891
• (en) J. S. Townsend et V. A. Bailey, « The motion of electrons in argon », Philosophical Magazine, vol. S.6, n^o 43,‎ 1922, p. 593-600
• (en) J. S. Townsend et V. A. Bailey, « The abnormally long free paths of electrons in argon », Philosophical Magazine, vol. S.6, n^o 43,‎ 1922, p. 1127-1128
• (en) J. S. Townsend et V. A. Bailey, « The motion of electrons in argon and in hydrogen », Philosophical Magazine, vol. S.6, n^o 44,‎ 1922, p. 1033-1052
• (en) J. S. Townsend et V. A. Bailey, « Motion of electrons in helium », Philosophical Magazine, vol. S.6, n^o 46,‎ 1923, p. 657-664
• (de) C. Ramsauer, « Über den Wirkungsquerschnitt der Gasmoleküle gegenüber langsamen Elektronen », Annalen der Physik, vol. 369, n^o 6,‎ 1921, p. 513-540 (DOI 10.1002/andp.19213690603)
• (de) C. Ramsauer, « Über den Wirkungsquerschnitt der Gasmoleküle gegenüber langsamen Elektronen. II. Fortsetzung und Schluß », Annalen der Physik, vol. 377, n^o 21,‎ 1923, p. 345-352 (DOI 10.1002/andp.19233772103)
• (en) David Bohm, Quantum Theory, Englewood Cliffs, New Jersey, Prentice-Hall, 1951
• (en) R. B. Brode, « The Quantitative Study of the Collisions of Electrons with Atoms », Rev. Mod. Phys., vol. 5,‎ 1933, p. 257
• (en) W. R. Johnson et C. Guet, « Elastic scattering of electrons from Xe, Cs⁺, and Ba²⁺ », Phys. Rev. A, vol. 49,‎ 1994, p. 1041
• (en) Nevill Francis Mott, The Theory of Atomic Collisions, Oxford, Clarendon Press, 1965, chap. 18