Dominance stochastique

La dominance stochastique globale du premier ordre stipule qu'une distribution est préférée à une autre si et seulement si la fonction de répartition de la distribution préférée n'est jamais supérieure et au moins une fois strictement inférieure à celle de l'autre distribution[1] - [2].

Une dominance stochastique est dite « d'ordre 1 » si, quelle que soit la valeur de la variable, l'une des fonctions ou distributions est systématiquement préférée à l'autre. Si un croisement des courbes s'opère et que, à partir d'une certaine valeur du paramètre qui est testé, la préférence s'inverse, on parle d'une dominance stochastique « d'ordre 2 »[3].

• Dominances stochastiques d'ordres 1 et 2
• 
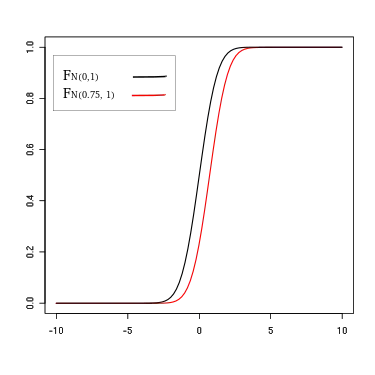  Exemple d'une dominance stochastique d'ordre 1.
• 
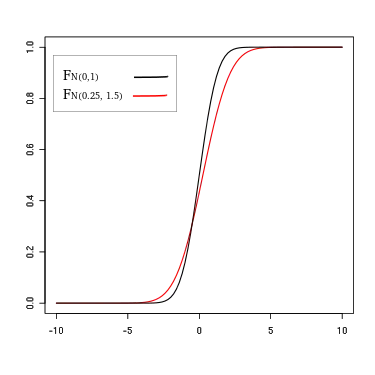  Exemple d'une dominance stochastique d'ordre 2.

La première évocation du concept de dominance stochastique est proposée par Frank Wilcoxon en 1945, puis, deux ans plus tard, dans un article de Henry B. Mann et Donald R. Whitney dans la revue The Annals of Mathematical Statistics en 1947[3].

En économie, le concept est popularisé par Michael Rothschild (en) et Joseph E. Stiglitz dans l'article Increasing risk: I. A definition par en 1970[4].

La dominance stochastique séquentielle fournit le cadre permettant d'effectuer des comparaisons statistiques, par exemple entre des pays dont les revenus et les pratiques de consommation des individus sont très différents[5] - [6].

Par ailleurs, l'approche par la dominance stochastique, dans le cadre d'un choix de politique publique, permet de vérifier en amont que ce choix puisse être conforme aux attentes d'un large éventail d'individus dotés de caractéristiques différentes en termes de revenus ou de redistribution[5].

En sciences sociales, les courbes de préférence sont souvent très proches, et la détermination de la dominance est donc complexe, rendant nécessaire la détermination de la significativité statistique de l'écart entre les deux[2].

Dans le cadre d'une décision impliquant une prise de risque, la théorie des perspectives montre que les individus ont une crainte de la perte supérieure à l'espoir du gain. Ce comportement peut être représenté par une combinaison convexe-concave de la fonction d'utilité[7].