Ensemble partiellement ordonné

Un ordre (ou ordre partiel) est une relation binaire sur un ensemble P qui est réflexive, antisymétrique et transitive. Elle se note ≤.

Les trois axiomes précédents se récrivent:

1. a ≤ a (réflexivité).
2. Si a ≤ b et b ≤ a, alors a = b (anti-symétrie).
3. Si a ≤ b et b ≤ c, alors a ≤ c (transitivité).

Ce n'est donc pas nécessairement un ordre total.

• L'ensemble des nombres entiers naturels, muni de la divisibilité est un ensemble partiellement ordonné infini.
• Un ensemble de personnes muni de la relation de la descendance généalogique est un ensemble partiellement ordonné. Par exemple, deux sœurs sont inférieures à leur mère mais ne sont pas comparables entre elles.
• L'ensemble des parties d'un ensemble donné, muni de l'inclusion forme un ensemble partiellement ordonné. Si l'ensemble donné est fini, son ensemble des parties est fini (plus précisément pour ${\displaystyle \#A=n}$, on a ${\displaystyle \#P(A)=2^{n}}$). La figure ci-dessous représente le diagramme de Hasse d'un ensemble à 3 éléments.

Diagramme de Hasse d'un ensemble à 3 éléments.

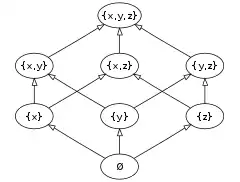
• Pour prendre un cas concret (en effet, isomorphe) de l’exemple précédent, un ensemble de personnes muni de la relation peut donner du sang pour forme un ensemble partiellement ordonné selon les systèmes ABO et Rhésus. Les éléments x, y, et z dans l’exemple précédent plus général étant instantiés par les antigènes A, B, et D (Rh+) de l’individu. Par exemple, un individu de groupe O+ peut donner à un receveur de groupe B+, mais aucun des deux peut ni donner à ni recevoir d’un individu de groupe A-.
• L'ensemble des nombres complexes muni de la relation d'ordre suivante est partiellement ordonné : ${\displaystyle a+ib<a'+ib'\Leftrightarrow \left\{{\begin{matrix}a<a'\\b<b'\end{matrix}}\right.}$.

Par exemple, on ne peut pas comparer 1 et i. Cet ordre n'est pas compatible avec la structure de corps de ${\displaystyle \mathbb {C} }$.

• L'ensemble des fonctions de ${\displaystyle \mathbb {R} }$ dans ${\displaystyle \mathbb {R} }$, muni de la relation d'ordre ${\displaystyle f<g}$ si ${\displaystyle \forall x,f(x)<g(x)}$, est un ensemble partiellement ordonné infini. Intuitivement, une fonction est plus petite qu'une autre si sa courbe est toujours en dessous de l'autre courbe. On peut généraliser cet exemple aux fonctions d'un ensemble X dans un ensemble partiellement ordonné P.
• L'ensemble des partitions d'un ensemble donné est partiellement ordonné, avec l'ordre donné par le raffinement des partitions : par définition, une partition est plus fine qu'une autre si elle fractionne les parties de l'autre en de plus petites parties.
• On peut munir ${\displaystyle R[X_{1},...,X_{n}]}$ l'ensemble des polynômes à n variables d'une relation d'ordre partiel. On commence par comparer les monômes à n variables via l'ordre lexicographique induit par ${\displaystyle 1<X_{1}<X_{2}<...<X_{n}}$ (cet ordre lexicographique est total). On compare deux polynômes ${\displaystyle P}$ et ${\displaystyle Q}$ en disant que ${\displaystyle P}$ est strictement plus petit que ${\displaystyle Q}$ si tout monôme non nul de ${\displaystyle P}$ est strictement plus petit que tout monôme non nul de ${\displaystyle Q}$. Cette relation d'ordre sur les polynômes est partielle.

Soit P un ensemble partiellement ordonné :

• Un élément a de P est un plus grand élément si pour tout élément b de P, b ≤ a. Un ensemble partiellement ordonné ne peut avoir qu’un plus grand élément.

• Un élément a de P est un élément maximal s’il n’existe pas d’élément b de P tel que b > a. Si P a un plus grand élément, il est l’unique élément maximal de P.

• Pour un sous-ensemble A de P, l’élément x de P est une borne supérieure de A si a ≤ x pour tout élément a de A. x n’appartient pas nécessairement à A. Le plus grand élément de P, s’il existe, est une borne supérieure de P.

Exemple : considérons l’ensemble des entiers positifs, ordonné par la division. 1 est le plus petit élément. En revanche cet ensemble ne possède pas de plus grand élément. Si on excluait maintenant l’élément 1, l'ensemble partiellement ordonné n’aurait plus de plus petit élément mais une infinité d’éléments minimaux : les nombres premiers.

Si E est un ensemble partiellement ordonné, il n'existe pas forcément de plus grand élément. Si E est un ensemble partiellement ordonné fini, il contiendra au moins un élément maximal. Si E est un ensemble inductif infini, on peut utiliser le lemme de Zorn pour avoir l'existence d'un élément maximal.

Certaines conditions sur les plus grands éléments et plus petits éléments d'un ensemble partiellement ordonné conduisent à la définition d'un treillis.

Par le même raisonnement on obtient le plus petit élément, les éléments minimaux et la borne inférieure.

Si a ≤ b ou a ${\displaystyle \geq }$ b, alors a et b sont comparables. Dans le diagramme de Hasse ci-dessus, {x} et {x,y,z} sont comparables, tandis que {x} et {y} ne le sont pas. Un ordre partiel dans lequel toute paire d’éléments est comparable est appelée un ordre total, et l’ensemble est appelé une chaîne.Un ensemble dans lequel on ne peut trouver de paire comparable s’appelle une antichaîne (par exemple l’ensemble {{x}, {y}, {z}} sur la figure ci-dessus)

On dit qu’un élément a est recouvert par un élément b, ce qui s’écrit a<:b, si a est strictement inférieur à b et qu’il n’existe pas d’élément c s’intercalant entre les deux. Par exemple, {x} est recouvert par {x,z} dans la figure ci-dessus mais pas par {x,y,z}.

Une classe importante de complexes simpliciaux provient d'ensembles partiellement ordonnés finis. On définit le complexe d'ordre D(P) d'un ensemble partiellement ordonné fini P comme étant l'ensemble des chaînes de P. Le complexe d'ordre est trivialement un complexe simplicial.

L'étude du ensemble partiellement ordonné donne des informations sur son complexe d'ordre, et donc il est intéressant d'étudier un complexe simplicial comme le complexe d'ordre d'un ensemble partiellement ordonné.

Dans le but de supprimer la multiplicité des relations d'ordre possibles lors ensemble partiellement ordonné, on peut définir trois règles différentes:

• L'ordre lexicographique:   (a,b) ≤ (c,d) si a < c ou (a = c et b ≤ d);
• L'ordre multiplicatif:   (a,b) ≤ (c,d) si a ≤ c et b ≤ d;
• La clôture réflexive du produit direct: (a,b) ≤ (c,d) si (a < c et b < d) ou (a = c et b = d).

Toutes ces règles s'appliquent également pour des produits de plus de deux ensembles partiellement ordonnés.