Distribution multimodale
En probabilités et statistique, une distribution multimodale est une distribution statistique présentant plusieurs modes.
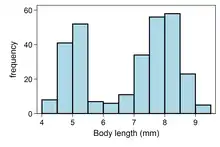
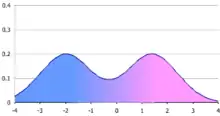
Éléments de contexte
Les distributions multimodales sont rencontrées dans divers domaines :
- les sondages d’opinion,
- la production industrielle[1], qui cherche généralement à éviter les phénomènes multimodaux souvent révélateurs d’un facteur d’influence non maîtrisé dans le processus,
- les phénomènes liés à la climatologie, à l'analyse du débit des rivières[2], à la géologie[3]…
Deux approches peuvent être adoptées suivant le besoin de l’observateur :
- L’approche « apprentissage et re-prédiction » :
- L’observateur cherche à établir la loi de probabilité du phénomène étudié sur la base d’observations expérimentales, dans le but de re-prédictions dans un contexte différent de celui de l’apprentissage.
- Que la distribution soit multimodale ou non ne change pas la façon de l’exploiter, comme n’importe quelle densité de probabilité ou fonction de répartition.
- L’approche plus « analytique » où l’observateur souhaite comprendre la raison de la multimodalité, en décomposant par exemple la loi de probabilité observée en la superposition de lois élémentaires unimodales, chacune s’appliquant avec une occurrence qui lui est propre. Ce processus d’identification peut être puissant vis-à-vis du diagnostic, mais également source de pièges.
Le second point de vue s'appuie sur les principales propriétés des mélanges de lois.
Le cadre étudié est celui des variables aléatoires continues (ou variables aléatoires à densité).
Explications informelles
Ce qu’indique la multimodalité d’une distribution
La multimodalité d’une distribution indique deux possibilités :
- l’échantillon n’est pas homogène, mais composé de plusieurs familles d’individus présentant des caractéristiques différentes[4],
- le phénomène observé présente plusieurs réponses, suffisamment distinctes pour qu’elles émergent du bruit naturel, l’occurrence de chacune de ces réponses étant stable dans le temps.
A contrario, l'unimodalité d'une distribution ne constitue pas en soi une preuve d’homogénéité de l’échantillon : un échantillon peut être hétérogène vis-à-vis d’une caractéristique donnée, sans que cela ne fasse émerger plusieurs modes sur la variable aléatoire étudiée.
À titre de contre-exemple, soit un échantillon composé de :

- 50% d’individus suivant une loi normale de moyenne et d’écart-type
- 50% d’individus suivant une loi normale de moyenne et d’écart-type
Bien que cet échantillon soit hétérogène par construction, la distribution résultante ne présente qu’un mode, certes plus étendu que ceux des deux distributions normales à l’origine de la réponse d’ensemble, mais l'effet de l’hétérogénéité reste noyé dans le bruit naturel apporté par les variances des deux lois normales de base.
Partant du contre-exemple précédent, la bimodalité de la distribution résultante apparaît si l'on « écarte » davantage les deux lois normales :
- en diminuant la moyenne de la première loi
- et en augmentant celle de la deuxième loi
- les deux écarts-types restant inchangés
Le paramètre clé qui fait apparaître (ou non) la bimodalité de la loi résultante est le biais réduit, c'est-à-dire le paramètre
Il n'y a pas de lien immédiat entre le nombre de composants présents dans un mélange et le nombre de modes de la densité de probabilité résultante.
Une distribution multimodale est-elle la somme de distributions unimodales ?
Le mélange de lois unimodales permet, sous certaines conditions, de créer un grand nombre de distributions multimodales (sens direct).
En revanche, retrouver – à partir de la donnée de la distribution multimodale – les lois unimodales qui la composent - et leurs occurrences associées - est une entreprise plus ardue (sens inverse) : la décomposition, toujours possible, n'est pas unique.
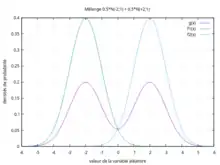
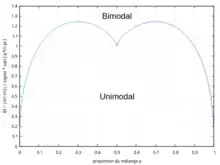
Pour illustrer la non-unicité d'une telle décomposition, soit la distribution bimodale donnée par les deux figures ci-contre (courbe en violet). Cette distribution bimodale peut être vue comme le mélange de :
- une distribution uniforme d'étendue [-4 ;-1] d'occurrence 20% et une distribution unimodale (courbe verte, dont l'abscisse du mode est située à environ 0,9) d'occurrence 80%,
- une distribution unimodale (courbe verte, dont l'abscisse du mode est située à environ -1) d'occurrence 40% et d'une distribution unimodale (courbe bleue, dont l'abscisse du mode vaut 1) d'occurrence 60%.
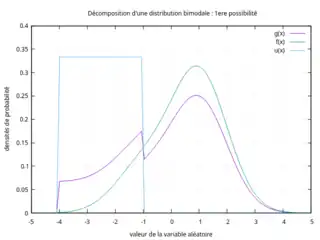 1re possibilité de décomposition
1re possibilité de décomposition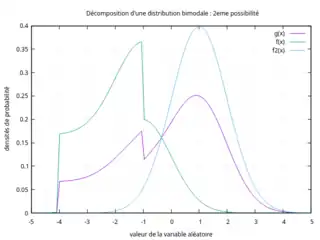 2e possibilité de décomposition
2e possibilité de décomposition
Terminologie
Homoscédastique
Se dit d'échantillons dont la variance est uniforme.
Mode mineur, majeur et antimode
Lorsque deux modes sont inégaux (c'est-à-dire que la densité de probabilité ne présente pas la même valeur pour ces deux modes) :
- le plus grand mode est appelé mode majeur,
- l'autre, le mode mineur,
- la valeur la moins fréquente entre les modes est appelée antimode.
Mélange de deux lois unimodales (sens direct)
Le mélange de deux distributions unimodales constitue un moyen de générer des distributions bimodales, à condition que l'écartement des modes de ces lois de base soit grand devant les variances de ces dernières.
Les propriétés du mélange peuvent être déterminées à partir de celles des lois unimodales de base employées et de leurs occurrences.
X désigne la variable aléatoire continue étudiée.
Dans ce sens direct, les 2 distributions de base sont connues, ainsi que leurs occurrences associées :
| Caractéristiques | Distribution no 1 | Distribution no 2 |
|---|---|---|
| Densité de probabilité | f1 (x) | f2 (x) |
| Fonction de répartition | F1 (x) | F2 (x) |
| Espérance (ou moyenne) | m1 | m2 |
| Variance | σ12 | σ22 |
| Occurrence | p1 | p2 = 1-p1 |
Les distributions impliquées peuvent être quelconques : aucune hypothèse n’est faite sur la normalité ou non de ces lois.
Loi de distribution du mélange
Soient g(x) la densité de probabilité recherchée, et G(x) la fonction de répartition associée.
L’application des probabilités conditionnelles permet d’écrire :
D'où l'expression de la densité de probabilité du mélange :
Cette densité de probabilité est convenablement normée, puisque son intégrale sur le domaine de définition de X capture l'ensemble des effectifs :
Le même raisonnement s'applique sur la fonction de répartition du mélange :
- Espérance du mélange
Connaissant désormais l'expression de la densité de probabilité du mélange, le calcul de l'espérance s'effectue comme suit :
Le résultat trouvé correspond à l'intuition : l'espérance du mélange est le barycentre des espérances de chaque loi pondéré par leur occurrence.
- Variance du mélange
Par indépendance, la moyenne des carrés est une forme linéaire des occurrences et :
Le carré de l'espérance vaut :
D'où l'expression de la variance du mélange - toujours sous la condition :
Cette expression montre que tout écart sur les moyennes, quel que soit son signe, contribue à augmenter la variance du mélange.
L'écart type du mélange s'obtient par sa définition habituelle :
Mélange de deux distributions unimodales identiques mais simplement décalées
Ce cas de figure est fréquent, et présente une propriété intéressante permettant de retrouver les occurrences (p1 et p2=1-p1) par simple lecture de la densité de probabilité du mélange.
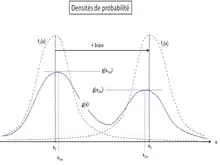
Ce cas particulier est caractérisé par :
- est la densité de probabilité d'une distribution unimodale :
- son mode est rencontré en
- l'occurrence de cette distribution est
- L'autre densité est obtenue par translation des abscisses de de la valeur d'un biais uniforme (noté ) :
- de même,
- le mode de est rencontré en
- l'occurrence de cette distribution est
Si le biais est suffisant, le mélange de ces deux distributions est bimodal. Soient :
- la densité de probabilité du mélange
- l'abscisse du premier mode de
- l'abscisse du second mode de
La propriété intéressante de ce cas de figure est que le rapport des deux maxima de la fonction donne le rapport des deux occurrences :
Mélange de deux distributions normales
Il s'agit d'un autre cas de figure suffisamment fréquent pour que ce mélange ait été étudié en détail[5].
La loi régissant la distribution du mélange de deux lois normales possède 5 paramètres :
- la moyenne de la première loi normale
- l'écart-type de la première loi normale
- la moyenne de la seconde loi normale
- l'écart-type de la seconde loi normale
- l'occurrence de la première loi, celle de la seconde étant une conséquence
Conditions de bimodalité du mélange
Les conditions nécessaires et suffisantes pour que le mélange de distributions normales soit bimodal ont été identifiées par Ray et Lindsay[6].
Une condition nécessaire pour qu'un mélange homoscédastique de deux distributions normales - i.e. dont les écarts-types sont égaux - soit bimodal est que leurs moyennes diffèrent d'au moins 2 fois l'écart-type commun[7].
Conditions d'unimodalité du mélange
Une condition suffisante pour l'unimodalité du mélange est que[8]:
- Cas homoscédastique
Une condition suffisante pour l'unimodalité du mélange dans le cas où les deux variances sont identiques est que[8]:
Une condition nécessaire et suffisante pour l'unimodalité du mélange est que[9]:
Soit : ou bien
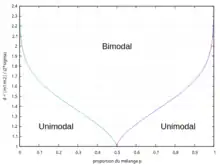
Cas où les deux occurrences sont égales (p1 = p2 = 0,5)
Une condition nécessaire et suffisante pour l'unimodalité du mélange est que[7]:
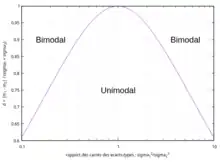
Soient et le facteur de séparation
La densité du mélange est unimodale si et seulement si
- Remarques
- Si les deux écarts-types sont égaux, et l'on retrouve le critère d'espacement des moyennes de moins de 2 fois l'écart-type commun.
- Le critère est inchangé si l'on permute et :
- tend vers lorsque l'un des 2 écarts-types devient prépondérant par rapport à l'autre :
- La séparation des domaines uni/bimodal suivant cette condition est représentée par la figure 10.
Mélange de n lois (sens direct)
Le raisonnement peut être étendu au cas du mélange de lois quelconques.
Les expressions de la densité de probabilité , de la fonction de répartition , de l'espérance et de la variance du mélange sont les suivantes :
Toujours sous la condition liant les occurrences :
Les conditions d'émergence de modes multiples sont plus complexes à formuler que dans le cas du mélange de 2 lois.
Statistiques descriptives
Les distributions bimodales constituent des exemples typiques où les paramètres classiques des statistiques descriptives (moyenne, médiane, écart-type) peuvent se révéler insuffisants, voire trompeurs :
- la valeur de la moyenne (comme celle de la médiane) peut être située dans des classes creuses, ne représentant ainsi pas une valeur typique,
- l'écart-type cumule ceux des distributions impliquées dans le mélange et celui résultant du biais de moyenne (cf. sections précédentes).
Bien que plusieurs soient suggérées, il n'existe actuellement aucune statistique descriptive universellement acceptée pour quantifier les paramètres d'une distribution multimodale dans le cas général.
Rapport bimodal et amplitude de la bimodalité
En cas de distribution bimodale avérée, deux métriques peuvent être définies[10] pour caractériser les différences d'amplitude entre les deux pics sur la densité de probabilité, obtenue en pratique par l'histogramme des effectifs observés par intervalles de valeurs sur la grandeur d'intérêt.
Le rapport bimodal [10] est défini comme le rapport des pics droit (indice r comme right) et gauche (indice l comme left) :
où désigne la densité de probabilité de la distribution bimodale étudiée, l'abscisse du pic droit, l'abscisse du pic gauche.
Cette quantité indique lequel des deux pics domine, donc une indication sur les proportions du mélange .
L'amplitude de la bimodalité [10] est définie par le rapport suivant :
est toujours compris entre 0 et 1. Plus grande est sa valeur, plus les pics sont émergents[10].
Séparation bimodale
Cet indice suppose que la distribution observée est un mélange de deux distributions normales et .
Les articles[10] et[11] introduisent la métrique de séparation bimodale définie comme suit :
D'autres auteurs lui préfèrent :
Ces métriques reviennent à la définition du « biais de moyenne réduit » - cf. section Explications informelles. Elles quantifient l'écartement des deux pics par rapport aux variances « naturelles » des 2 distributions normales constituant le mélange, l'idée étant que les deux pics doivent être suffisamment écartés pour qu'émerge le caractère bimodal du mélange.
Outre la restriction au mélange de distributions normales, on peut objecter à ces deux métriques que :
- Lorsque l'observateur fait face à ses données brutes (histogramme des effectifs), il ne connaît généralement pas les 5 paramètres constitutifs du mélange de 2 lois normales , nécessaires pour calculer ces métriques.
- Que les proportions du mélange n'interviennent pas dans ces formules proposées, alors que ces proportions interviennent dans les conditions d'unimodalité / multimodalité du mélange (cf. section Mélange de 2 distributions normales).
- Lorsque l'observateur a identifié ces 5 paramètres par une méthode inverse, il n'a plus besoin de statistiques descriptives pour guider sa démarche d'identification.
Indice de Wang
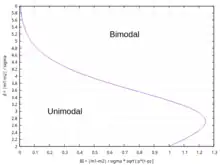
Cet indice de bimodalité proposé par l'article[12] suppose que la distribution observée résulte du mélange de deux distributions normales d'égales variances (cas homoscédastique), de moyennes différentes, dans des proportions différentes. Cet indice est défini comme suit :
Cet indice a du sens dans la mesure où :
- Il résume le rapport des variances, entre celle du mélange et celle des 2 lois normales :
- Il constitue une combinaison des 4 paramètres propres à ce type de mélange, et permettant de retrouver la séparation des domaines uni/bimodal vue précédemment (cf. Mélange de 2 distributions normales) - cf. figures 11 et 12.
Bien que la définition de cet indice incorpore la proportion de mélange , elle n'est pas suffisante pour capter tous les effets de cette proportion sur le comportement du mélange (cf. figure 11) et réduire ainsi l'analyse d'une dimension.
Cet indice est sujet aux mêmes objections que celles formulées à l'encontre des critères de séparation bimodale.
Mesure de l’accord (A) suivant Van der Eijk
Les travaux de Cees van der Eijk portent sur les comportements politiques comparés et leur méthode de mesure. Les distributions multimodales sont fréquentes dans ce domaine : elles révèlent différents groupes d’opinion.
Considérations liminaires
Dans son article référencé[13], l’auteur :
- rappelle que les métriques classiques (moyenne, écart-type) sont insuffisantes pour appréhender les distributions multimodales, car elles ne représentent pas convenablement ce qu'elles sont censées mesurer : la localisation des pics et leur acuité.
- propose une mesure de l’accord (Agreement) caractéristique d’un histogramme donné, une fois ce dernier décomposé en composantes élémentaires (ou « couches ») et pour lesquelles l'accord peut être exprimé de manière simple et sans équivoque.
La variable aléatoire examinée consiste en une échelle de notation à niveaux (ou rating scale). Si la variable aléatoire originelle est continue (variable à densité), il faut diviser son domaine en classes d’égale étendue.
En matière de sondages d’opinion, le nombre de niveaux est nécessairement limité pour des raisons pratiques liées au questionnaire, mais doit rester suffisamment élevé pour permettre une bonne résolution sur les écarts entre individus. Les échelles de 7, 9, 10 ou 11 points sont couramment pratiquées, cadre dans lequel s’inscrit la mesure de l’Accord.
L’échelle de l’Accord est adimensionnelle. L’auteur l’a construite de façon à respecter 3 niveaux caractéristiques :
- La borne supérieure représente l’accord parfait : toutes les observations sont situées dans une seule classe de l’échelle de notation (quelle que soit la valeur associée à cette classe).
- La borne intermédiaire représente l’absence d’accord : les observations sont équiréparties sur toutes les classes (distribution uniforme).
- La borne inférieure représente le désaccord maximal : les deux classes extrêmes de l’échelle de notation accueillent chacune la moitié des observations.
Analyse des distributions semi-uniformes
La méthode de Van der Eijk s’appuie sur une distribution élémentaire : la distribution semi-uniforme, dans laquelle les différentes classes offertes par l’échelle de notation sont soit vides, soit équipeuplées.
Une telle distribution est complètement caractérisée par :
- son effectif total
- son motif : i.e. comment sont distribuées les classes vides et les classes non-vides.
Le motif est représenté par un K-uplet de valeurs binaires : 0 représente une classe vide, 1 représente une classe non-vide.
Une distribution semi-uniforme est unimodale si et seulement si toutes les classes non-vides (i.e. les séquences de 1) sont contiguës.
Dans le cas contraire, où des 0 s’intercalent entre deux classes non-vides, la distribution semi-uniforme est multimodale.
Mesure de l’accord (A) pour les distributions semi-uniformes unimodales
La distribution étant unimodale, sa mesure d’unimodalité vaut 1 par construction de l'ensemble de la méthode.
Il reste alors à quantifier l’étendue des classes non-vides dans la plage permise par l’échelle de notation (à valeurs) pour obtenir la mesure de l’accord .
Soit le nombre de classes non-vides. L’auteur propose la forme linéaire suivante :
Cette expression réalise les conditions limites souhaitées :
- : lorsque toutes les observations sont situées dans une seule classe,
- : lorsque les observations sont équiréparties sur toutes les classes.
Toute étendue intermédiaire des classes non-vides aboutit à un accord compris entre 0 et 1, l’accord étant d’autant plus faible que l’on tend vers la distribution uniforme.
Remarquons que l’accord ne dépend que de l’étendue des classes non-vides contiguës, et non des valeurs de l’échelle de notation associées à cette localisation : sur une échelle de notation à 7 niveaux, les motifs et présentent la même valeur .
Mesure de l’accord (A) pour les distributions semi-uniformes multimodales
L’auteur propose de pondérer l’expression précédente de l’accord par une mesure d’unimodalité inférieure à 1, soit :
La mesure d’unimodalité est construite suivant le principe directeur selon lequel l’inclusion de nombreuses classes vides (0) entre deux séquences de classes non-vides (1), tendant à rejeter ces dernières sur les extrêmes de l’échelle de notation (à K niveaux), traduit :
- non pas l’absence d’accord,
- mais la manifestation d’un désaccord : , avec -1 comme valeur extrême.
La mesure d’unimodalité est évaluée par la méthode suivante :
Recensement des triplets de type (110), (011) ou (101) contenus dans le motif
L’évaluation de l’unimodalité demande de recenser tous les triplets constitués de deux « 1 » et d’un « 0 » parmi le K-uplet représentant le motif de la distribution semi-uniforme.
désignant toujours le nombre de classes non-vides, il représente le nombre de « 1 » contenus dans le motif. Le nombre de triplets recherchés vaut :
Catégorisation de ces triplets
- Les triplets de type ou sont conformes à l’unimodalité : soit le nombre de triplets répondant à ce type.
- Les triplets de type dévient de l’unimodalité : soit le nombre de triplets répondant à ce type.
Évaluation de la mesure d’unimodalité (U)
L’auteur propose d’évaluer la mesure de l’unimodalité par la formule suivante :
Remarques :
Cette mesure d’unimodalité tend vers 1 (distribution unimodale) lorsque tend vers 0 : pas de triplets de type déviant de l’unimodalité.
Le cas de bimodalité extrême est atteint lorsque les deux classes non-vides sont rejetées sur les bords du motif , auquel cas :
- La mesure d’unimodalité vaut
- L’accord vaut :
Décomposition d’un histogramme en couches de distributions semi-uniformes
L’histogramme réel contenant les observations n’a pas de raison de se conformer au modèle théorique de la distribution semi-uniforme défini précédemment.
En revanche, toute distribution (portant sur une échelle de notation à K niveaux) peut être décomposée sous la forme d’au plus couches de distributions semi-uniformes[13].
Le principe de cette décomposition consiste :
- À localiser la classe la moins représentée de l’histogramme, permettant de construire une première distribution uniforme : son accord est nul.
- Puis localiser la deuxième classe la moins représentée, permettant de construire une deuxième distribution semi-uniforme, avec une classe vide à l’endroit vidé par la première distribution. Son accord est évalué par la méthode décrite précédemment.
- Et ainsi de suite… jusqu’à avoir capturé tous les individus de l’histogramme.
La valeur finale de l’accord est obtenue par la somme pondérée des accords de chaque couche par son poids dans la distribution totale. Le poids est défini comme le rapport des effectifs de la ième couche sur les effectifs totaux.
Ce mécanisme de décomposition est illustré par la figure ci-dessous :
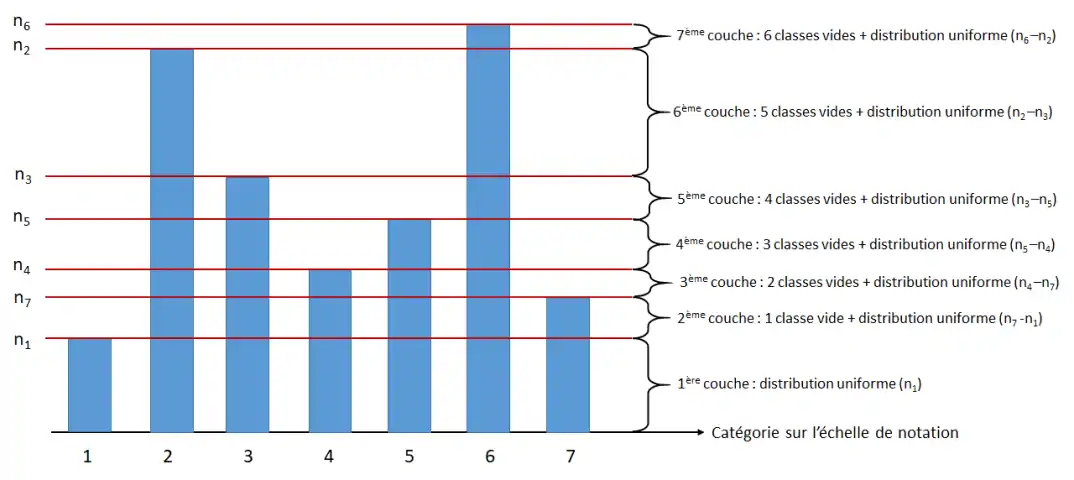
Mise en œuvre de la méthode
Sur la base de l'exemple donné en Figure 13 :
La décomposition des effectifs de l'histogramme en 7 couches de distributions semi-uniformes est effectuée comme suit :
Ceci permet d'accéder à la représentation en motifs et poids pour chaque couche, et d'effectuer les calculs des mesures d'unimodalité et de l'Accord :
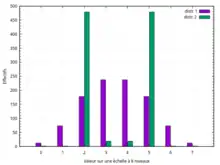
Un autre exemple montre deux distributions portant sur la même variable (échelle de notation à 8 niveaux) :
- dont les moyennes sont identiques, et les écarts-types très similaires,
- mais évaluées comme différentes par l'Accord de Van der Eijk, car la première est unimodale alors que la seconde possède un caractère bimodal fortement marqué (Figure 14).
Avantages et limites de la méthode
| Avantages | Limites |
|---|---|
La méthode est autoporteuse :
|
Nécessité de former des classes d'égale étendue, ce qui peut limiter la portée de la méthode, ou causer une perte d'information. |
La méthode distingue les 2 cas :
|
Aucune règle ne permet de définir un intervalle de confiance autour de l'Accord , puisque l'auteur ne définit pas la statistique qui régit cet Accord. |
| Point d'attention :
La comparaison de deux distributions (sur la base de l'accord ) n'a de sens que si l'échelle comporte le même nombre de points . |
Méthode d'Otsu
La méthode d'Otsu propose de déterminer un seuil de séparation entre deux modes à partir d'un histogramme des effectifs d'une distribution d'origine donnée. Le seuil de séparation jugé pertinent suivant cette méthode est celui qui minimise les variances intra-classes, donc celui qui maximise la variance inter-classes[14].
Cette méthode, utilisée en traitement d'image, aboutit à un résumé binaire de la distribution d'origine, avec perte d'information. Cette méthode est d'autant plus pertinente que la distribution d'origine présente un caractère bimodal affirmé.
Notes et références
- 14:00-17:00, « ISO 22514-8:2014 », sur ISO (consulté le )
- « A.12 - Mode et distribution multimodale - Wikhydro », sur wikhydro.developpement-durable.gouv.fr (consulté le )
- « Distribution bimodale des altitudes et mobilité horizontale (dérive) des continents — Planet-Terre », sur planet-terre.ens-lyon.fr (consulté le )
- « Distribution Multimodale », sur www.statsoft.fr (consulté le )
- C. A. Robertson et J. G. Fryer, « Some descriptive properties of normal mixtures », Scandinavian Actuarial Journal, vol. 1969, nos 3-4, , p. 137–146 (ISSN 0346-1238 et 1651-2030, DOI 10.1080/03461238.1969.10404590, lire en ligne, consulté le )
- Surajit Ray et Bruce G. Lindsay, « The topography of multivariate normal mixtures », The Annals of Statistics, vol. 33, no 5, (ISSN 0090-5364, DOI 10.1214/009053605000000417, lire en ligne, consulté le )
- (en) M. Schilling, A. Watkins et W. Watkins, « Is Human Height Bimodal? », undefined, (lire en ligne, consulté le )
- Javad Behboodian, « On the Modes of a Mixture of Two Normal Distributions », Technometrics, vol. 12, no 1, , p. 131–139 (ISSN 0040-1706 et 1537-2723, DOI 10.1080/00401706.1970.10488640, lire en ligne, consulté le )
- (en) Hajo Holzmann et Sebastian Vollmer, « A likelihood ratio test for bimodality in two-component mixtures with application to regional income distribution in the EU », AStA Advances in Statistical Analysis, vol. 92, no 1, , p. 57-69 (DOI 10.1007/s10182-008-0057-2, lire en ligne, consulté le )
- Chidong Zhang, Brian E. Mapes et Brian J. Soden, « Bimodality in tropical water vapour », Quarterly Journal of the Royal Meteorological Society, vol. 129, no 594, , p. 2847–2866 (ISSN 0035-9009 et 1477-870X, DOI 10.1256/qj.02.166, lire en ligne, consulté le )
- Keith A. Ashman, Christina M. Bird et Stephen E. Zepf, « Detecting bimodality in astronomical datasets », The Astronomical Journal, vol. 108, , p. 2348 (ISSN 0004-6256, DOI 10.1086/117248, lire en ligne, consulté le )
- Jing Wang, Sijin Wen, W. Fraser Symmans et Lajos Pusztai, « The Bimodality Index: A criterion for Discovering and Ranking Bimodal Signatures from Cancer Gene Expression Profiling Data », Cancer Informatics, vol. 7, , CIN.S2846 (ISSN 1176-9351 et 1176-9351, DOI 10.4137/cin.s2846, lire en ligne, consulté le )
- (en) Cees Van der Eijk, « Measuring Agreement in Ordered Rating Scales », Quality & Quantity, Kluwer Academic Publishers, 35 (3): 325–341., (lire en ligne)
- (en) D. Chaudhuri et A. Agrawal, « Split-and-merge Procedure for Image Segmentation using
Bimodality Detection Approach », Defence Electronics Application Laboratory, Dehradun-248 001, (lire en ligne
 )
)



































































































































