Distance entre deux droites gauches
Dans l'espace muni de la distance euclidienne, la distance entre deux droites gauches est la plus courte distance séparant deux droites qui ne se coupent pas et ne sont pas parallèles[alpha 1] - [1].
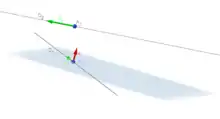
Formule de la distance
Soient :
- une droite affine passant par et de vecteur directeur ;
- une droite affine passant par et de vecteur directeur , avec et non parallèles;
- , vecteur orthogonal à et (le symbole est celui du produit vectoriel).
La distance entre et est égale à:
- ,
ce qui correspond à la norme de la projection orthogonale de sur .
Remarques :
- si les droites sont sécantes, elles sont coplanaires et le produit scalaire précédent est nul ;
- la formule n’est pas valable pour des droites parallèles, car le dénominateur serait alors nul, dans ce cas on utilisera la formule de la distance d'un point à une droite[1] :
- ou .
Recherche des points les plus proches
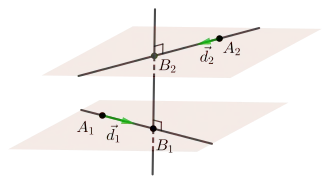
Comme et sont gauches, elles admettent une unique perpendiculaire commune , qui coupe en et en . La longueur est également la distance [1]. Pour trouver ces points il faut combiner les propriétés suivantes :
- appartient à ;
- appartient à ;
- est perpendiculaire à ;
- est perpendiculaire à .
Ou, mathématiquement :
- ;
- ;
- ;
- .
Comme , le report de cette égalité dans les deux dernières relations conduit à deux équations linéaires à deux inconnues et .
On peut se passer de la résolution d'un système en utilisant des vecteurs (resp. ) orthogonaux à qui soit également, pour l'un orthogonal à et pour l'autre orthogonal à .
On peut prendre, par exemple, et
ou bien[2], sans mobiliser de produit vectoriel, et (ces derniers vecteurs sont colinéaires aux précédents).
Les conditions et se traduisent alors par :
- et
et fournissent les valeurs de et :
- et
En géométrie hyperbolique
En géométrie hyperbolique, un résultat formellement identique est le théorème des ultraparallèles : deux droites du plan hyperbolique ultraparallèles (qui ne se coupent pas et ne sont pas parallèles asymptotes) admettent une unique perpendiculaire commune, et la distance entre les pieds de cette perpendiculaire est la distance minimale entre les deux droites.
Notes et références
Notes
- Les droites gauches n'existent que dans les espaces euclidiens de dimension supérieure à deux (dans le plan, deux droites sont nécessairement sécantes ou parallèles); le résultat est d'ailleurs vrai en toute dimension supérieure à 3, car deux droites de définissent n sous-espace affine de dimension 3.
Références
- Fred Lang, Géométrie analytique, Yverdon-les-bains, , 61 p. (lire en ligne [PDF]), p. 30.
- Renzo Cairoli, Algèbre linéaire, PPUR presses polytechniques, coll. « architecture - Enseignement des mathématiques », (présentation en ligne), p. 76-77








































