Dimension (théorie des graphes)
En mathématiques, et plus particulièrement dans la théorie des graphes, la dimension d'un graphe est le plus petit nombre entier tel qu'une représentation classique du graphe[1] dans l'espace affine euclidien de dimension ne comporte que des segments de longueur 1.
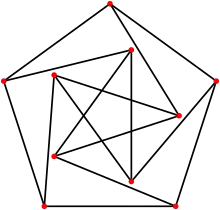
Dans cette définition, les sommets doivent être distincts, mais il n'y a pas de contraintes sur le croisement des arêtes. On note la dimension d'un graphe ainsi : .
Par exemple, le graphe de Petersen peut être tracé avec des segments de longueur 1 sur le plan euclidien , mais pas sur la droite : sa dimension est 2 (figure).
Cette notion a été introduite en 1965 par Paul Erdős, Frank Harary et William Tutte[2]. Elle généralise à une dimension quelconque la notion de graphe distance-unité du plan .
Exemples
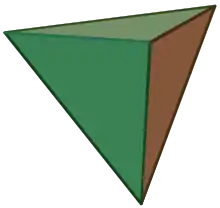
Graphe complet
Dans le pire des cas pour un graphe, tous les sommets sont reliés, c'est le graphe complet.
Il faut un espace euclidien de dimension pour y plonger le graphe complet à sommets pour que toutes les arêtes soient de longueur 1. Par exemple, il faut 2 dimensions pour le graphe complet à 3 sommets représenté par un triangle équilatéral, 3 dimensions pour le graphe complet à 4 sommets représenté par un quadrilatère régulier (figure), etc.
Dit autrement, la dimension du graphe complet coïncide avec la dimension du simplexe associé.

Graphes bipartis complets
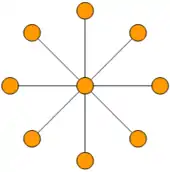
Tous les graphes étoile , pour sommets périphériques, sont de dimension 2 (figure) : ils ont besoin d'un plan pour être tracés avec des arêtes de longueur 1. Les graphes étoile à 1 et 2 sommets périphériques n'ont besoin que d'une droite (dimension 1).
La dimension d'un graphe biparti complet , pour , vaut 3 : sur la figure, on voit comment placer sommets sur un même cercle et les 2 sommets restants sur l'axe de ce cercle. peut quant à lui se tracer avec un losange dans un plan.
La dimension d'un graphe biparti complet général , pour et , vaut 4.
En résumé :
- , selon les valeurs de et de
Dimension et nombre chromatique
Théorème — La dimension de n'importe quel graphe est toujours inférieure ou égale au double de son nombre chromatique :
Dimension euclidienne


La notion de dimension d'un graphe présentée plus haut ne satisfait pas complètement certains auteurs. En effet :
- si deux sommets de sont reliés par une arête, alors leur représentation les place à 1 unité de distance ;
- en revanche, si dans la représentation, deux sommets sont à une unité de distance, ils ne sont pas forcément reliés dans le graphe.
La figure ci-contre montre le problème dans le cas d'un graphe roue à un sommet central et 6 sommets périphériques auquel on a retiré un des rayons. Sa représentation dans le plan admet deux sommets à distance 1, mais qui ne sont pas reliés.
Alexander Soifer définit en 1991 la dimension euclidienne d'un graphe[4]. Avant lui, en 1980, Paul Erdős et Miklós Simonovits l'avaient déjà définie sous le nom de dimension fidèle (faithful dimension)[5]. La dimension euclidienne d'un graphe est le nombre entier tel que dans une représentation classique de dans l'espace à dimensions , deux sommets du graphe sont reliés si et seulement si leurs représentations sont à une distance de 1.
On note cette dimension . Elle est toujours plus élevée que la dimension définie plus haut :
Ainsi, dans l'exemple du graphe roue auquel on a enlevé une arête radiale, si l'on exclut que des sommets non reliés puissent être à une distance de 1, il faut sortir un sommet du plan (illustration).
Dimension euclidienne et degré maximal
Paul Erdős et Miklós Simonovits ont démontré en 1980 le résultat suivant[5] :
Théorème — La dimension euclidienne de n'importe quel graphe est inférieure ou égale au double de son degré maximal plus un :
Notes et références
- Dans la représentation classique d'un graphe, les sommets sont représentés par des points et les arêtes par des segments de droite.
- (en) P. Erdős, F. Harary et W. T. Tutte, « On the dimension of a graph », Mathematika, no 12, , p. 118 à 122 (lire en ligne)
- Le principe de cette preuve est dû à Lenz en 1955 ; il ne l'a pas publiée et on ne la connaît que par Paul Erdős.
- (en) Alexander Soifer, The Mathematical Coloring Book, Springer, (ISBN 978-0-387-74640-1)
- (en) P. Erdős et M. Simonovits, « On the chromatic number of geometric graphs », Ars Comb., no 9, , p. 229 à 246
































![{\displaystyle [A_{1}A_{2}]}](https://img.franco.wiki/i/41bbcf9571621ee6021b17f0c44cd862f4cdd64a.svg)















