Cubique du triangle
Une cubique du triangle est une courbe cubique plane passant par plusieurs points remarquables du triangle.
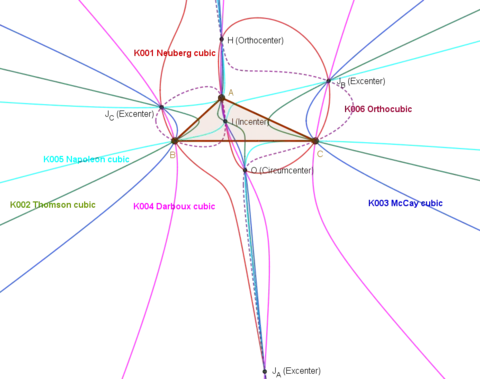
Histoire
Émile Lemoine a étudié plusieurs de ces cubiques en 1900[1].
Bernard Gibert, mathématicien français, a créé une encyclopédie en ligne des cubiques du triangle répertoriant 1280 courbes (au ) avec leurs équations barycentriques, les centres du triangle appartenant à la courbe et les propriétés géométriques de la courbe[2].
Cas particuliers
Isocubique
Pour un triangle ABC et un point P dans le plan du triangle, on appelle isocubique ou cubique isogonale pivotale ou cubique pK-isogonale la courbe cubique des points M tels que M, P et le conjugué isogonal de M par rapport à ABC sont alignés. Le centre de conjugaison est appelé pivot.
Elle passe nécessairement par les centres des cercles inscrit et exinscrits du triangle de référence[3].
Cubique isotomique pivotale
Pour un triangle ABC et un point P dans le plan du triangle, on appelle cubique isotomique pivotale la courbe cubique des points M tels que M, P et le conjugué isotomique de M par rapport à ABC sont alignés. Le centre de conjugaison est appelé pivot.
Exemples
Cubique de Darboux
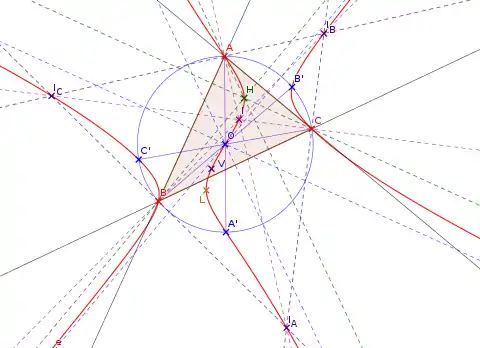
La cubique de Darboux d'un triangle est l'ensemble des points dont le triangle pédal est en homologie avec le triangle de référence.
C'est une cubique auto-isogonale dont le point pivot est le point de Longchamps du triangle de référence. Son centre de symétrie est le centre du cercle circonscrit au triangle.
La cubique de Darboux passe par dix points remarquables du triangle : ses trois sommets, les centres de ses cercles circonscrit, inscrit et exinscrits, son orthocentre, son point de Longchamps, son point de Bevan et leurs conjugués isogonaux[4].
Son équation trilinéaire est, pour un triangle de côtés a = BC, b = AC, c = AB, et d'angles aux sommets A, B, C :
Cubique de Neuberg
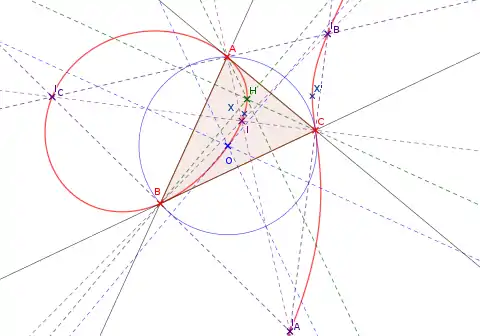
La cubique de Neuberg d'un triangle est une cubique auto-isogonale dont le point pivot est le point à l'infini d'Euler (Nombre de Kimberling X30) du triangle de référence. Elle est formée par tous les points P tels que, pour le conjugué isogonal P* de P, la droite (PP*) soit parallèle à la droite d'Euler du triangle.
La cubique de Neuberg passe par dix points remarquables du triangle : ses trois sommets, les centres de son cercle circonscrit, de son cercle inscrit et de ses cercles exinscrits, son orthocentre, ses points de Fermat, ses points isodynamiques, le point à l'infini d'Euler et leurs conjugués isogonaux[5]. Dans certains articles, elle est même désignée sous le nom de "conique des 21 points" ou "conique des 37 points". Neuberg l'a étudié dans son Mémoire sur le tétraèdre dans le cadre des "quadrangles involutifs"[6].
Son équation trilinéaire est, pour un triangle de côtés a = BC, b = AC, c = AB, et d'angles aux sommets A, B, C :
Cubique de Lucas
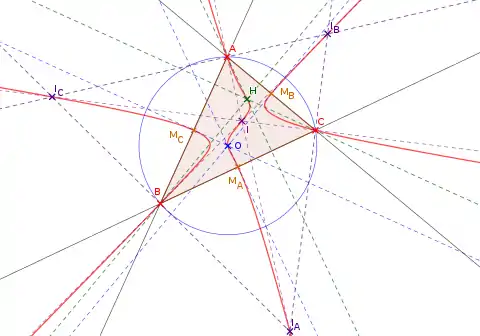
La cubique de Lucas est une cubique isotomique pivotale, de pivot le conjugué isotomique de l'orthocentre (nombre de Kimberling X69).
Elle désigne tous les points dont la polaire trilinéaire est orthogonale à la droite passant par ce point et le centre du cercle circonscrit.
La cubique de Lucas passe par 16 points remarquables du triangle : ses trois sommets, les trois milieux de ses côtés, les centres de son cercle circonscrit, de son cercle inscrit et ses cercles exinscrits, son orthocentre, les milieux de ses hauteurs et son point de Lemoine[7].
Son équation barycentrique est, pour un triangle de côtés a = BC, b = AC, c = AB :
Si un point P est sur la cubique de Lucas du triangle, le point Q tel que le triangle cévien de P est le triangle pédal de Q est sur sa cubique de Darboux[8].
Cubique de Lemoine
La cubique de Lemoine est une cubique définie comme les points telles que les intersections des céviennes passant par ces points et des médiatrices des côtés du triangle sont alignées. Le nom de cubique de Lemoine a été donné par Joseph Neuberg[9].
Elle passe par les sommets du triangle, son orthocentre, les milieux de ses côtés et le centre de son cercle circonscrit.
Les points d'intersection de la cubique et du cercle circonscrit au triangle sont aux sommets du triangle et de son triangle normal circonscrit.
Les asymptotes de cette cubique sont parallèles à celles de l'orthocubique, la cubique isogonale pivotale de pivot l'orthocentre.
Cubique de McKay
La cubique de McKay, du nom de Brendan Damien McKay, ou cubique de Griffiths, est une cubique auto-isogonale, de pivot le centre du cercle circonscrit, qui est le lieu des points dont le cercle pédal touche le cercle d'Euler du triangle de référence.
La cubique de McKay est le lieu des points pour lesquels les cercles pédaux et circumcéviens sont orthologiques[10].
Cubique de Thomson
La cubique de Thomson est une cubique auto-isogonale, de pivot le centre de gravité. C'est le lieu des centres des coniques circonscrites au triangle dont les normales aux sommets sont concourantes.
La cubique de Thomson est aussi appelée cubique des dix-sept points, car elle passe par les sommets, les milieux de ses côtés, les milieux de ses hauteurs, les centres des cercles circonscrit, inscrit et exinscrits, le centre de gravité, l'orthocentre et le point de Lemoine du triangle ; elle passe aussi par le mittenpunkt du triangle[11].
Références
- Émile Lemoine, « Suite de théorèmes et de résultats concernant la géométrie du triangle », Extrait des Comptes rendus de l’Association française pour l’avancement des sciences Congrès de Paris, (lire en ligne)
- (en) « Cubics in the Triangle Plane - Home Page »
- (en) Eric W. Weisstein, « Pivotal Isogonal Cubic », sur MathWorld
- (en) Eric W. Weisstein, « Darboux Cubic », sur MathWorld
- (en) Eric W. Weisstein, « Neuberg Cubic », sur MathWorld
- (en) Abdilkadir Altınta, « On Some Properties Of Neuberg Cubic », International Journal of Computer Discovered Mathematics, vol. 5, , p. 22-49 (ISSN 2367-7775)
- Bulletin de l'APMEP n°420, janvier/février 1999
- (en) Eric W. Weisstein, « Lucas Cubic », sur MathWorld
- (en) Bernard Gibert, « The Lemoine cubic and its generalizations », Forum Geometricum, vol. 2, (lire en ligne).
- (en) Eric W. Weisstein, « M'Cay Cubic », sur MathWorld
- (en) Eric W. Weisstein, « Thomson Cubic », sur MathWorld
Liens externes
- (en) Eric W. Weisstein, « Triangle Cubic », sur MathWorld
- Bernard Gibert, Catalog of Triangle Cubics, 2010-2016, archive


