Point de Longchamps
cercle de Longchamps
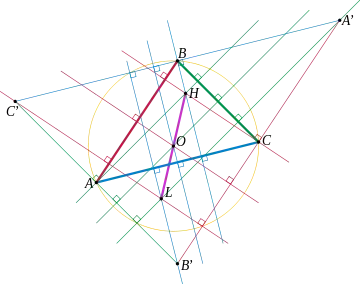
Dans la géométrie du triangle, le point de Longchamps d'un triangle est un élément du triangle nommé d'après le mathématicien français Gaston Albert Gohierre de Longchamps. Il peut être vu comme l'image de l'orthocentre du triangle par rapport au centre du cercle circonscrit. Son nombre de Kimberling est X(20)[1].
Point de Longchamps
Définition
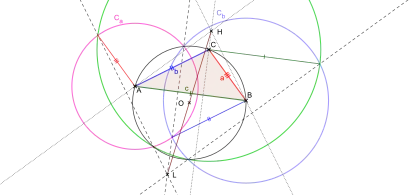
On note les sommets du triangle étudié A, B et C, et les longueurs des côtés opposés respectivement a, b et c, selon la notation standard en géométrie du triangle. Dans son article de 1886 dans lequel il présente le point, de Longchamps le définit comme le centre d'un cercle Δ orthogonal à trois cercles Δa, Δb et Δc, avec Δa centré en A et de rayon a, et ainsi de suite pour les deux autres cercles. De Longchamps met aussi en évidence que le même point, qu'on appelle désormais point de Longchamps, peut également être défini comme l'orthocentre du triangle anticomplémentaire de ABC, et comme l'image de l'orthocentre de ABC par la symétrie centrale autour du centre du cercle circonscrit du même triangle[2].
Le cercle de Steiner d'un triangle est concentrique avec le cercle d'Euler et son rayon vaut 1,5 fois le rayon du cercle circonscrit du triangle ; le point de Longchamps est le centre d'homothétie du cercle de Steiner et du cercle circonscrit[3].
Propriétés supplémentaires
Par la symétrie de l'orthocentre autour du centre du cercle circonscrit, le point de Longchamps est aligné avec ces points et appartient donc également à la droite d'Euler du triangle. Ces points sont donc alignés également avec le centre de gravité et le centre du cercle d'Euler[1] - [3] - [4].
Le point de Longchamps est également aligné avec le centre du cercle inscrit et le point de Gergonne du triangle, sur une droite différente de la droite d'Euler[1] - [5]. Les trois cercles centrés en A, B et C, de rayons respectifs s–a, s–b et s–c (avec s est le demi-périmètre) sont tangents deux à deux, et il existe deux autres cercles tangents à ces trois cercles, les cercles de Soddy intérieur et extérieur ; les centres de ces deux cercles appartiennent tous deux à la droite passant par le point de Longchamps et le centre du cercle inscrit[1] - [3]. Le point de Longchamps est le point d'intersection de cette droite avec la droite d'Euler, et avec trois autres droites définies de façon similaire, passant non pas par le centre du cercle inscrit mais les centres des cercles exinscrits du triangle[3] - [5].
La cubique de Darboux peut être définie à partir du point de Longchamps, comme le lieu des points X tels que X, le conjugué isogonal de X et le point de Longchamps sont alignés. C'est la seule cubique invariante du triangle qui est à la fois son propre conjugué isogonal et avec une symétrie centrale (son centre de symétrie est le centre du cercle circonscrit du triangle)[6]. Le point de Longchamps appartient à cette courbe, tout comme l'orthocentre, qui est son image[1].
Cercle de Longchamps
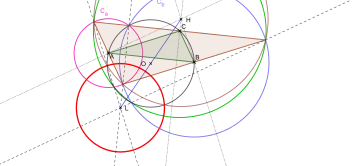
Pour un triangle obtusangle, le cercle de Longchamps est le cercle radical des cercles de puissance de ce triangle, soit le cercle orthogonal au trois cercles de puissance du triangle (les cercles centrés au milieu d'un côté et passant par le 3e sommet du triangle. Son centre est le point de Longchamps du triangle, et il passe par les points d'intersection des cercles circonscrits au triangle et à son triangle anticomplémentaire[7].
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « De Longchamps point » (voir la liste des auteurs).
- Clark Kimberling, « X(20) = de Longchamps point », sur Encyclopedia of Triangle Centers.
- G. de Longchamps, « Sur un nouveau cercle remarquable du plan du triangle », Journal de Mathématiques spéciales, vol. 5, , p. 57–60 (lire en ligne). Voir section 4, "détermination du centre de Δ", pp. 58–59.
- A. Vandeghen, « Mathematical Notes: Soddy's Circles and the De Longchamps Point of a Triangle », The American Mathematical Monthly, vol. 71, no 2, , p. 176–179 (DOI 10.2307/2311750, JSTOR 2311750, MR 1532529).
- H.S.M. Coxeter, « Some applications of trilinear coordinates », Linear Algebra and its Applications, vol. 226/228, , p. 375–388 (DOI 10.1016/0024-3795(95)00169-R
 , MR 1344576). Voir la Section 5, "Six notable points on the Euler line", pp. 380–383.
, MR 1344576). Voir la Section 5, "Six notable points on the Euler line", pp. 380–383. - (en) Michael Longuet-Higgins, « A fourfold point of concurrence lying on the Euler line of a triangle », The Mathematical Intelligencer, vol. 22, no 1, , p. 54–59 (DOI 10.1007/BF03024448, MR 1745563).
- Bernard Gibert, « K004 Darboux cubic = pK(X6,X20) : Cubics in the Triangle Plane »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?).
- Jean-Louis Aymé, « Gaston Albert Gohierre de Longchamps dans les journaux scientifiques »
(en) Nathan Altshiller-Court, « On the De Longchamps circle of the triangle », The American Mathematical Monthly, Taylor & Francis, Ltd., vol. 33, no 7, , p. 368-375 (lire en ligne)
Liens externes
- (en) Eric W. Weisstein, « de Longchamps Point », sur MathWorld
- (en) Eric W. Weisstein, « de Longchamps Circle », sur MathWorld