Code de Reed-Solomon
Le code de Reed-Solomon est un code correcteur basé sur les corps finis dont le principe est de construire un polynôme formel à partir des symboles à transmettre et de le suréchantillonner. Le résultat est alors envoyé, au lieu des symboles originaux. La redondance de ce suréchantillonnage permet au récepteur du message codé de reconstruire le polynôme même s'il y a eu des erreurs pendant la transmission.
Histoire
Ce code est dû à Irving S. Reed et Gustave Solomon[1]. Il a notamment été utilisé pour le codage des CDs[2].
Vue d'ensemble

Soient m, n, k, t des nombres entiers strictement positifs tels que . Généralement, on prend m = 8 (parfois m = 16), n = 255, k = 239, t = 8. Les codes Reed-Solomon sont des codes par bloc. En effet ils prennent en entrée un bloc de données de taille fixée k, chaque donnée étant un symbole élément du corps fini possédant éléments. On ajoute à ce bloc 2t symboles de contrôle, formant ainsi un bloc de sortie de taille fixée égale à n. Ainsi, on a :
- m : nombre de bits par symbole. Dans le cas où m = 8, les symboles sont des octets.
- k : nombre de symboles d’information, appelé charge utile ;
- 2t : nombre de symboles de contrôle ou de redondance ;
- n: nombre de symboles transmis (charge utile et contrôle).
Grâce à l'ajout des symbôles de contrôle, ces codes permettent de corriger deux types d'erreurs :
- les erreurs induisant une modification des données, où certains bits passent de la valeur 0 à la valeur 1 et vice versa comme sur le canal binaire symétrique ;
- les erreurs provoquant des pertes d'informations aussi appelées effacements, lorsque des paquets d'informations sont perdus ou effacés comme sur le canal binaire à effacement.
On note un codage de Reed-Solomon ou .
Si la localisation des erreurs n'est pas connue à l'avance — ce qui est le cas en pratique — le codage Reed-Solomon sait corriger t erreurs.
n étant souvent trop important en pratique, une partie des informations peut être remplacée par des zéros avant codage et ne sera pas transmise, mais devra être ajoutée avant décodage. On parle dans ce cas de code Reed-Solomon raccourci (« shortened Reed-Solomon codes »).
On peut également concevoir des codes de Reed-Solomon sur des corps finis quelconques.
Un exemple de code de Reed-Solomon
Il existe plusieurs variantes[4] - [5] - [6] du code de Reed-Solomon, développées au cours des dernières décennies dans le but de rendre de plus en plus rapides les procédés de codage et de décodage. Une des variantes possibles est présentée ici.
L'information à transmettre
Soit un message A constitué de k symboles éléments du corps fini . Ce corps est de caractéristique 2, ce qui signifie qu'il satisfait à la règle de calcul 1 + 1 = 0, ou encore 1 = -1, ou encore qu'il n'y a pas de distinction entre somme et différence. Il possède par ailleurs un élément dit primitif ayant la propriété suivante :
- Les éléments forment une base de en tant qu'espace vectoriel de dimension m sur le corps .
- engendre le groupe multiplicatif de
Ainsi, les éléments non nuls de peuvent s'écrire comme combinaisons linéaires de à coefficients dans {0,1}, mais aussi comme une puissance de , entre 0 et .
Les k symboles constituant le message A sont considérés comme les coefficients d'un polynôme de degré inférieur ou égal à k-1, i.e. un élément de . Ce polynôme est l'information à transmettre et sera encore noté .
Le codage
On appelle polynôme générateur le polynôme de degré 2t défini de la façon suivante :
Ce polynôme admet pour racines les .
On définit le polynôme de contrôle comme étant le reste de la division euclidienne de par Ce polynôme est de degré strictement inférieur à 2t. Les coefficients de ce polynôme forment le code de contrôle de l'information A.
On définit alors le polynôme . Ce polynôme est de degré inférieur ou égal à . Il possède la propriété de s'annuler en . (rappel : on est toujours dans un corps de caractéristique 2, donc + et - ont le même effet)
La transmission du message
Les coefficients du polynôme sont transmis au destinataire. Au cours de cette transmission, des erreurs portant sur certains coefficients peuvent se produire, et le destinataire reçoit des coefficients formant un polynôme .
Le destinataire teste alors si, pour tout i entre 1 et 2t, on a bien . Si c'est le cas, il considère qu'il n'y a eu aucune erreur de transmission et que . Il retrouve l'information A dans les k-1 coefficients des termes de degrés les plus élevés du polynôme .
Si au moins l'un des est non nul, il y a eu erreur de transmission sur au moins l'un des coefficients. Cependant, le destinataire considère que le nombre de coefficients affectés est inférieur ou égal à t. Sous cette hypothèse, il va être capable de reconstituer le message C initial.
La correction des erreurs
Si est différent de , soit , polynôme de degré inférieur ou égal à n-1, et comportant un nombre de coefficients non nuls. Par hypothèse, on suppose que est inférieur ou égal à t. Posons :
- , et , les étant des indices distincts pouvant varier entre 0 et n-1.
est pour le moment inconnu du destinataire. Il s'agit pour celui-ci de déterminer :
- Le nombre d'erreurs ,
- les rangs où sont situées ces erreurs,
- les valeurs de ces erreurs.
Une fois ces informations reconstituées, le destinataire sera en mesure de déterminer le polynôme et de reconstituer le message initial . Pour cela, on suit les cinq étapes suivantes.
1) Calcul des syndromes : On calcule les 2t quantités , appelées syndromes. Comme et que les sont nuls, on a également :
On dispose ainsi de 2t équations dont les inconnues et sont au plus au nombre de 2t. Cependant, le système n'est pas linéaire et sa résolution est technique.
2) Détermination du nombre d'erreurs : On considère le polynôme dont les racines sont les inverses des . Ce polynôme se développe sous la forme . On peut vérifier que les coefficients , inconnus du destinataire, satisfont un système linéaire de équations, la j-ème équation étant, pour j variant de 1 à :
en effet :
De plus, la plus grande valeur inférieure ou égal à t pour laquelle le déterminant de ce système est non nul est précisément le nombre égal au nombre d'erreurs transmises. On part donc de , et si le déterminant est nul, on décrémente jusqu'à obtenir un déterminant non nul.
3) Détermination de l'emplacement des erreurs : Une fois ainsi déterminé, on résout le système, ce qui définit le polynôme . On cherche les racines de ce polynôme, dont les inverses donnent les valeurs des . Pour chaque r entre 1 et , on cherche la puissance de telle que . On a ainsi déterminé les rangs des erreurs transmises.
4) Détermination de la valeur des erreurs : Les étant désormais connus, on peut résoudre le système dont l'équation générale est et dont les inconnues sont les , permettant de déterminer les valeurs de ces inconnues. Ce sont les valeurs des erreurs commises.
5) Correction du message reçu : Connaissant les et les , on connaît le polynôme et donc le message initial
Les erreurs d'effacement
Si l'information est inscrite sur un support comme un CD ou un DVD, il peut se produire des erreurs d'effacement. L'erreur est précisément localisée mais on ne peut lire aucune information à cet endroit. On peut cependant reconstituer les symboles effacés en s'aidant là aussi des équations données par les syndromes. Comme les localisations sont connues, que les inconnues sont les seules valeurs et qu'on dispose de 2t équations, on peut corriger l'effacement de symboles.
Applications
Stockage de données
Pour le CD, on utilise 2 codages de Reed-Solomon (code CIRC pour Cross Interleaved Reed-Solomon Code). On code une première fois avec un code C1 = RS(28, 24), puis on entrelace (ceci permet de répartir l'information afin de mieux résister aux trains d'erreurs consécutives que peut provoquer une rayure qui détruit beaucoup d'octets localement), ensuite on code à nouveau les données entrelacées avec un code C2 = RS(32, 28). L'idée est que le premier code permet d'éliminer le bruit ambiant mais s'il ne peut corriger (par exemple, s'il y a une salve d'erreurs), il efface le bloc (car on peut corriger deux fois plus d'effacements que de caractères faux) et ensuite le code est désentrelacé. Ainsi la perte d'information est diluée sur une grande plage de données ce qui permet au code de corriger ces effacements.
Pour le DVD le principe est le même que pour les CD, on a un code PI= RS(182, 172) et un code PO = RS(208, 192)
Transmission par satellite
Pour le DVB, le codage est RS(204, 188, t=8)
Exemple
pour le DVB, le codage est RS(204, 188, t=8)
Pour 188 (=k) octets en entrée, on ajoute 16(=2 t) octets de correction d'erreur, ce qui donne 204 en sortie du codeur.
8 octets (=t) sur 204 peuvent être corrigés.
Si plus de 8 octets sont détectés comme erronés, le bloc de données utiles est marqué comme défectueux. Aucune erreur n'est alors corrigée
Faiblesse
En raison du faible nombre de symboles que le codage Reed-Solomon peut corriger, ce codage est très mauvais en cas de bruit impulsif de longue durée, ou de bruit aléatoire régulier.
- Pour la transmission de données (ADSL, DVB-T), le bruit impulsif peut être dû à des moteurs, relais, lampes à décharge ou tubes d'éclairage, clôture électrique...
- Pour le stockage de données (CD, DVD), le bruit impulsif peut être dû à une rayure sur le support.
Utilisation dans un modem avec codeur convolutif
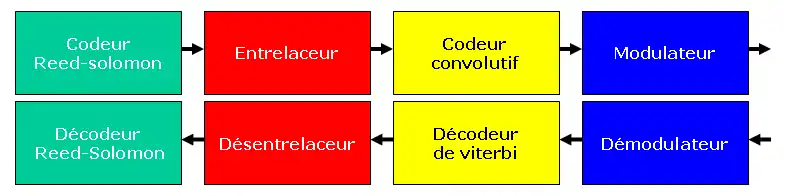
En général, en émission, dans un modem (ADSL, modem satellite IDR/SMS, DVB-S, etc ), le codage Reed-Solomon, renforcé par un entrelaceur est accompagné d'un codeur convolutif. En réception, les erreurs résiduelles non corrigées par le décodeur de Viterbi seront alors désentrelacées dans les blocs d'origines et corrigées par le décodeur Reed-Solomon dans la mesure de son pouvoir correcteur.
Le but du désentrelaceur est de remplacer en réception, une salve d'erreurs regroupées et souvent non corrigeables (bruit impulsif) par une multitude d'erreurs réparties et souvent corrigeables pour le décodeur de Reed-Solomon.
Liens externes
- Code Reed-Solomon Principes et programmation du code Reed-Solomon en Java.
- William Geisel, Tutorial on Reed–Solomon Error Correction Coding, NASA, Technical Memorandum (1990)
Références
- (en) I. S. Reed, G. Solomon, « Polynomial codes over certain finite fields », J. Soc. Indus. Appl. Math., no 8, , p. 300-304
- Pascal Boyer, Petit compagnon des nombres et de leurs applications, Calvage et Mounet, , 648 p. (ISBN 978-2-916352-75-6), VI. Cryptographie, chap. 8.4 (« Codes BCH »), p. 560-562.
- (en) « NASA Beams Mona Lisa to Lunar Reconnaissance Orbiter at the Moon », sur nasa.gov
- (en) D. Gorenstein, N. Ziegler, « D class of error-correcting codes in symbols », J. Soc. Indus. Math. Appl., no 9, , p. 207-2014
- (en) W. W. Peterson, « Encoding and error-correction procedures for the Bose-Chaudhuri codes », IRE Trans. Inform. Theory, no IT-6, , p. 459-470
- (en) Maria Bras-Amoros, « A decoding approach to Reed-Solomon codes from their definition », Amer. Math. Monthly, vol. 125, no 4, , p. 320-338









![{\displaystyle \mathbb {F} _{2^{m}}[X]}](https://img.franco.wiki/i/cc774efda0bed6a92dc023f3a718f62c0ae03e1c.svg)





































