Code d'effacement

Le contrôle de la parité est un cas spécial où ${\displaystyle n=k+1}$. Depuis un ensemble de ${\displaystyle k}$ valeurs ${\displaystyle \{v_{i}\}_{1\leq i\leq k}}$, une somme de contrôle est calculée et ajoutée aux ${\displaystyle k}$ valeurs sources :

${\displaystyle v_{k+1}=-\sum _{i=1}^{k}v_{i}.}$

L'ensemble des k + 1 valeurs ${\displaystyle \{v_{i}\}_{1\leq i\leq k+1}}$ est cohérent par rapport à la somme de contrôle. Si l'une de ces valeurs, ${\displaystyle v_{e}}$, est effacée, elle peut être retrouvée facilement en sommant les variables restantes tel que :

${\displaystyle v_{e}=-\sum _{i=1,i\neq e}^{k+1}v_{i}.}$

Dans le cas simple où k = 2, les symboles redondants peuvent être créés par échantillonnage de différents points le long de la ligne entre deux symboles originaux. Ceci est présenté grâce à un exemple simple appelé err-mail:

Alice veut envoyer son numéro de téléphone (555629) à Bob en utilisant err-mail. Err-mail fonctionne comme l'e-mail sauf que :

1. Approximativement la moitié du courrier est perdue.
2. Les messages plus grand que 5 caractères sont interdits.
3. Le prix est prohibitif (comme pour le courrier par avion)

Au lieu de demander à Bob d'acquitter les messages qu'elle envoie, Alice invente le schéma suivant.

1. Elle découpe son numéro de téléphone en 2 parties a = 555, b = 629, et envoie 2 messages - "A = 555" et "B = 629" – a Bob.
2. Elle construit une fonction linéaire, ${\displaystyle f(i)=a+(b-a)(i-1)}$, dans le cas présent ${\displaystyle f(i)=555+74(i-1)}$, tel que ${\displaystyle f(1)=555}$ et ${\displaystyle f(2)=629}$.

Code d'effacement optimal 1

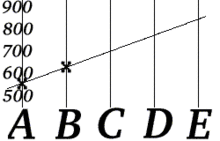
1. Elle calcule les valeurs f(3), f(4), et f(5), puis transmet 3 messages redondants : "C = 703", "D = 777" et "E = 851".

Bob sait que f(k) est défini par ${\displaystyle f(i)=a+(b-a)(i-1)}$, où a et b sont les deux parties de son numéro de téléphone.

Maintenant, supposons que Bob reçoive "D = 777" et "E = 851".

Code d'effacement optimal 2

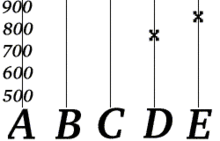
Bob peut retrouver le numéro de téléphone d'Alice en calculant les valeurs de a et b à partir des valeurs (f(4) et f(5)) qu'il a reçu. Bob peut effectuer cette procédure en utilisant n'importe quel couple de deux valeurs err-mail, donc le code d'effacement de cet exemple a un taux de 40%.

Notons qu'Alice ne peut pas coder son numéro de téléphone dans une seule valeur err-mail, car il contient six caractères, et la longueur maximum d'un message err-mail est de cinq caractères. Si elle envoie son numéro de téléphone en morceaux, demandant à Bob d'acquitter la réception de chacun de ces morceaux, il faudrait au moins quatre messages pour l'envoyer de toute façon (deux d'Alice et deux acquittements de Bob). Donc, le code d'effacement dans cet exemple, qui requiert cinq messages, est économique.

Cet exemple est bien sûr inventé dans le cas présent. Pour qu'un vrai code d'effacement générique fonctionne sur n'importe quel jeu de données, nous aurions besoin de quelque chose de plus pertinent que la fonction f(i).

La construction linéaire ci-dessus peut être généralisée en interpolation polynomiale. De plus, les points sont calculés dans un corps fini.

Premièrement, on choisit un corps fini F d'ordre minimum n, usuellement une puissance de 2. L'émetteur énumère les symboles de données de 0 à k-1 et les envoie. Il construit ensuite un polynôme de Lagrange p(x) d'ordre k tel que p(i) est égal au symbole de donnée i. Puis, il envoie p(k),...,p(n-1). Le récepteur peut alors utiliser une interpolation polynomiale pour retrouver les paquets perdus, à condition qu'il reçoive k symboles correctement. Si l'ordre de F est inférieur à 2^b, ou b est le nombre de bits d'un symbole, alors plusieurs polynômes peuvent être utilisés.

L’émetteur peut construire les symboles k à n-1 « à la volée », c'est-à-dire distribuer la charge de travail de manière égale entre la transmission des symboles. Si le récepteur veut faire ses calculs « à la volée », il peut construire un nouveau polynôme q, tel que q(i) = p(i) si le symbole i < k est reçu correctement et q(i) = 0 quand le symbole i < k n'a pas été reçu. Maintenant, soit r(i) = p(i) − q(i). En premier lieu, nous savons que r(i) = 0 si le symbole i < k a bien été reçu. Ensuite, si le symbole i >= k a été reçu correctement, alors r(i) = p(i) − q(i) peut être calculé. Donc nous avons suffisamment de points de données pour construire r et l’évaluer afin de trouver les paquets manquants. Donc l’émetteur et le récepteur ont besoin tous deux de o(n (n − k)) opérations et seulement o(n − k) d'espace pour fonctionner « à la volée ».

Ce processus est implémenté par le code de Reed-Solomon, avec des mots construits dans un corps fini en utilisant le matrice de Vandermonde.

• codes Tornado
• LDPC

• codes en ligne
• codes LT
• codes Raptor

• Somme de contrôle: utilisé dans les systèmes de stockage RAID.
• Parchive
• Tahoe-LAFS includes zfec
• Code de Reed-Solomon
• Erasure Resilient Systematic Code, un code MDS dépassant les performances de Reed–Solomon en un nombre maximum de paquets redondants, voir RS(4,2) with 2 bits or RS(9,2) avec 3 bits
• Code régénérants[1].
• tout autre code MDS

• Alphabet radio