Secret réparti

Le secret réparti ou le partage de secret consiste à distribuer un secret, par exemple une clé ou un mot de passe, entre plusieurs dépositaires. Le secret ne peut être découvert que si un nombre suffisant de dépositaires mettent en commun les informations qu'ils ont reçues. En revanche, un nombre inférieur de dépositaire n’apporte aucune information sur le secret.

Blakley : Chaque partage de secret est un plan et le secret est le point d'intersection entre les trois partages. Deux partages se croisent seulement en une ligne d'intersection.

Shamir : 2 points suffisent à définir une droite, 3 une parabole, 4 une courbe cubique… et, de manière générale, k points pour un polynôme de degré k-1

Le secret réparti a été inventé indépendamment par Adi Shamir[1] et George Blakley[2] en 1979.

Principe

Plus formellement, n dépositaires reçoivent chacun une information différente. Si un groupe quelconque de t dépositaires parmi les n dépositaires mettent en commun leurs informations, ils retrouvent la donnée secrète. En revanche, un groupe de moins de t dépositaires ne doit rien pouvoir apprendre de la donnée secrète avec les informations dont ils disposent.

Xor

Si $n=t$ , c'est-à-dire si tous les dépositaires doivent être nécessaires pour retrouver la donnée secrète, la méthode la plus simple est le XOR. $n-1$ des informations distribuées sont seulement des chaînes aléatoires de la même taille que la donnée secrète, et le n-ième information est la somme XOR de la donnée secrète et des $n-1$ autres informations. Cette technique repose sur le même principe que le masque jetable.

Blakley

Dans un corps fini, on constitue un système linéaire à n équations et t inconnues, et dont la seule solution est la donnée secrète. Le terme constant est public, et chaque participant reçoit une ligne du système.

Shamir

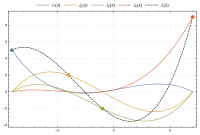
Dans un corps fini, on génère un polynôme de degré t dont le terme constant est la donnée secrète. On donne à chaque dépositaire les coordonnées d’un point distinct choisi sur la courbe. t dépositaires peuvent alors, par interpolation, retrouver les coefficients du polynôme, et donc la donnée secrète.

Notes et références

Adi Shamir, « How to Share a Secret », Commun. ACM, vol. 22,‎ 1^er novembre 1979, p. 612–613 (ISSN 0001-0782, DOI 10.1145/359168.359176, lire en ligne, consulté le 4 mars 2016)
(en) G. Blakley, « Safeguarding cryptographic keys », Proc. of the National Computer Conference,‎ 1979

Annexes

Articles connexes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.