Centre d'inertie

Caisse dans un camion constituant le référentiel ; pour déterminer si la force d'inertie ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {I} }}$ provoque le basculement (accélération linéaire ou force centrifuge), il faut connaître son point d'application. Dans le cas de droite, les droites d'action des forces ne sont pas concourantes, donc la stabilité en rotation n'est plus assurée.

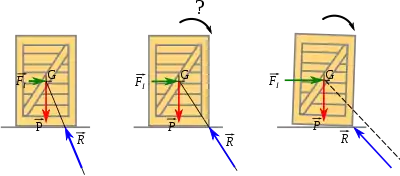
Considérons un véhicule muni de suspensions — motocyclette, voiture, autobus… — qui freine. On voit l'avant du véhicule plonger. À l'inverse, même si c'est moins visible, lorsque le véhicule accélère linéairement, l'avant se relève, ce qui permet par exemple aux deux-roues de faire des roues arrière.

Dans un virage, les véhicules à quatre roues s'inclinent vers l'extérieur du virage ; les deux-roues doivent se pencher vers l'intérieur pour éviter la chute.

Si un objet est posé sur le plancher du véhicule, toute accélération au sens large du terme — augmentation ou diminution de la vitesse, modification de la direction — peut provoquer sa chute.

Pour décrire ces effets en rotation, il faut pouvoir définir un point d'application aux effets d'inertie. En statique analytique, le principe fondamental de la dynamique en rotation s'exprime en général par rapport au centre de masse (puisque l'on a en général le moment d'inertie par rapport à G), cet effet d'inertie est alors masqué puisque son moment par rapport à ce point est nul. Ce n'est pas le cas si l'on considère le moment par rapport à un autre point, ou bien si l'on veut utiliser des méthodes de résolution graphiques.

Par ailleurs, pour une étude statique ou dynamique, toute force volumique qui s'exerce de manière uniforme peut se modéliser par un vecteur force s'appliquant au centre d'inertie. C'est le cas par exemple d'un objet en matériau ferromagnétique dans un champ magnétique uniforme.

Axe de rotation centré (gauche) et excentré (à droite)

Force centripète qu'exerce l'axe sur le disque excentré

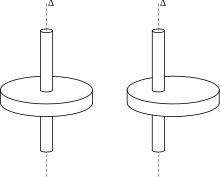
Considérons un disque que l'on veut faire tourner autour d'un axe Δ perpendiculaire à sa face, fixe dans le référentiel galiléen. Pour créer une accélération angulaire α donnée, l'effort à fournir est moindre si l'axe Δ passe par le centre d'inertie (figure de gauche) que s'il est excentré (figure de droite). Ceci se traduit par le théorème de Huygens pour le calcul du moment d'inertie.

Par ailleurs, lors de la rotation, si le centre d'inertie n'est pas sur l'axe, cela signifie que l'axe doit exercer une force sur le disque pour créer une accélération centrale centripète. Cette force tournant avec l'objet, cela crée des vibrations. Ces vibrations peuvent être créées volontairement, par exemple pour les vibreurs, ou bien être involontaires, auquel cas elles sont nuisibles : elles provoquent des bruits, de l'usure prématurée, le desserrage d'éléments vissés, un phénomène de fatigue pouvant amener à la rupture de l'axe, …

Pour un objet en rotation, la connaissance de la position du centre d'inertie est donc capitale pour déterminer l'axe de rotation idéal, notamment aux fréquences de rotation élevées.

On se place dans un référentiel galiléen R_g de repère ${\displaystyle (\mathrm {O} ,{\vec {x}},{\vec {y}},{\vec {z}})}$. Considérons deux points matériels discrets (M₁, m₁) et (M₂, m₂). Le point M₁ subit des forces dont la résultante — la somme vectorielle — est notée ${\displaystyle {\vec {\mathrm {F} }}_{1}}$ ; de même, ${\displaystyle {\vec {\mathrm {F} }}_{2}}$ désigne la résultante des forces sur M₂. Le système Σ est l'ensemble des deux points matériels : Σ = {(M₁, m₁) ; (M₂, m₂)} ; l'environnement de ce système est noté Σ (« complémentaire de sigma »).

Appliquons le principe fondamental de la dynamique à chaque point matériel :

${\displaystyle \left\{{\begin{aligned}m_{1}{\vec {a}}_{1}=\ &{\vec {\mathrm {F} }}_{1}\\m_{2}{\vec {a}}_{2}=\ &{\vec {\mathrm {F} }}_{2}\\\end{aligned}}\right.}$

L'accélération du centre de masse vaut

${\displaystyle {\vec {a}}_{\mathrm {G} }={\frac {\mathrm {d} ^{2}}{\mathrm {d} t^{2}}}{\overrightarrow {\mathrm {OG} }}={\frac {1}{m}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} t^{2}}}(m_{1}{\overrightarrow {\mathrm {OM} }}_{1}+m_{2}{\overrightarrow {\mathrm {OM} }}_{2})={\frac {1}{m}}(m_{1}{\vec {a}}_{1}+m_{2}{\vec {a}}_{2})}$

soit

${\displaystyle m{\vec {a}}_{\mathrm {G} }=m_{1}{\vec {a}}_{1}+m_{2}{\vec {a}}_{2}={\vec {\mathrm {F} }}_{1}+{\vec {\mathrm {F} }}_{2}}$.

On voit donc que le centre de masse se comporte comme un point matériel de masse m = m₁ + m₂ qui subirait l'ensemble des forces ${\displaystyle {\vec {\mathrm {F} }}_{1}+{\vec {\mathrm {F} }}_{2}}$ s'exerçant sur les points matériels du système Σ. Le centre d'inertie permet donc de simplifier l'étude du système.

La résultante ${\displaystyle {\vec {\mathrm {F} }}_{1}}$ des actions s'exerçant sur le point matériel M₁ peut se décomposer en ${\displaystyle {\vec {\mathrm {F} }}_{1}={\vec {\mathrm {F} }}_{\mathrm {ext/1} }+{\vec {\mathrm {F} }}_{2/1}}$ :

• ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {ext/1} }}$ est la résultante des actions qu'exerce l'extérieur du système Σ sur M₁ ; on le note également ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {{\bar {\Sigma }}/1} }}$, ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {ext\to 1} }}$ ou ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {{\bar {\Sigma }}\to 1} }}$ ;
• ${\displaystyle {\vec {\mathrm {F} }}_{2/1}}$ est la résultante des actions de M₂ sur M₁ ; il peut s'agir d'attraction gravitationnelle, électrostatique, d'action de contact (traction via un câble, poussée directe ou via une barre, …) ; on le note également ${\displaystyle {\vec {\mathrm {F} }}_{2\to 1}}$.

De même, on décompose ${\displaystyle {\vec {\mathrm {F} }}_{2}={\vec {\mathrm {F} }}_{\mathrm {ext/2} }+{\vec {\mathrm {F} }}_{1/2}}$. D'après le principe des actions réciproques (troisième loi de Newton), on a

${\displaystyle {\vec {\mathrm {F} }}_{2/1}=-{\vec {\mathrm {F} }}_{1/2}}$.

Il en résulte que

${\displaystyle {\vec {\mathrm {F} }}_{1}+{\vec {\mathrm {F} }}_{2}={\vec {\mathrm {F} }}_{\mathrm {ext/1} }+{\vec {\mathrm {F} }}_{2/1}+{\vec {\mathrm {F} }}_{\mathrm {ext/2} }+{\vec {\mathrm {F} }}_{1/2}={\vec {\mathrm {F} }}_{\mathrm {ext/1} }+{\vec {\mathrm {F} }}_{\mathrm {ext/2} }}$.

La résultante des actions s'exerçant sur le centre de gravité de Σ se réduit aux actions extérieures à Σ. Les forces internes au système Σ, les actions entre M₁ et M₂, « disparaissent du bilan »

On peut donc simplifier l'étude en étudiant le point matériel (G, m) comme substitut de l'ensemble Σ = {(M₁, m₁) ; (M₂, m₂)}. Les actions mécaniques s'exerçant sur (G, m) sont les actions extérieures s'exerçant sur Σ, c'est-à-dire les actions de Σ sur Σ.

L'extension au cas de n points se fait en considérant les propriétés mathématiques du barycentre.

Plaçons nous maintenant dans le référentiel du centre de masse R' de repère ${\displaystyle (\mathrm {G} ,{\vec {x}},{\vec {y}},{\vec {z}})}$. Les points matériels subissent des forces d'inertie ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {I1} }=-m_{1}{\vec {a}}_{\mathrm {G} }}$ et ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {I2} }=-m_{2}{\vec {a}}_{\mathrm {G} }}$. La résultante des forces sur le point matériel M₁ s'écrit :

${\displaystyle {\begin{aligned}{\vec {\mathrm {F} }}_{\mathrm {R1} }=\ &{\vec {\mathrm {F} }}_{1}+{\vec {\mathrm {F} }}_{\mathrm {I1} }\\=\ &{\vec {\mathrm {F} }}_{1}-{\frac {m_{1}}{m}}({\vec {\mathrm {F} }}_{1}+{\vec {\mathrm {F} }}_{2})\\=\ &{\frac {1}{m}}(m{\vec {\mathrm {F} }}_{1}-m_{1}{\vec {\mathrm {F} }}_{1}-m_{1}{\vec {\mathrm {F} }}_{2})\\=\ &{\frac {1}{m}}(m_{2}{\vec {\mathrm {F} }}_{1}-m_{1}{\vec {\mathrm {F} }}_{2})\\\end{aligned}}}$.

Pour le point matériel M₂, cela s'écrit :

${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {R2} }={\frac {1}{m}}(m_{1}{\vec {\mathrm {F} }}_{2}-m_{2}{\vec {\mathrm {F} }}_{1})}$.

On voit que dans ce référentiel a priori non galiléen, les points matériels sont soumis à des forces de résultantes opposées et de même intensité : ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {R1} }=-{\vec {\mathrm {F} }}_{\mathrm {R2} }}$.

Notons qu'ici,

${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {R1} }={\vec {\mathrm {F} }}_{2/1}+{\frac {1}{m}}(m_{2}{\vec {\mathrm {F} }}_{\mathrm {ext/1} }-m_{1}{\vec {\mathrm {F} }}_{\mathrm {ext/2} })}$

comme nous étudions « l'intérieur » du système Σ, il est normal que l'on retrouve les actions intérieures à Σ.

Si les points matériels sont liés par une barre indéformable de masse négligeable — la distance M₁M₂ est constante —, alors Σ constitue ce que l'on appelle un « solide indéformable ». Dans le référentiel du centre de masse R', le solide Σ a un mouvement de rotation autour d'un axe instantané passant par G, puisque les distances GM₁ et GM₂ sont elles aussi constantes — l'orientation de l'axe peut varier au cours du temps. On peut donc définir un vecteur vitesse angulaire instantanée ${\displaystyle {\vec {\omega }}}$ tel que la vitesse des points matériel dans R' vaut :

${\displaystyle {\vec {v'}}_{1}={\overrightarrow {\mathrm {M_{1}G} }}\wedge {\vec {\omega }}}$

${\displaystyle {\vec {v'}}_{2}={\overrightarrow {\mathrm {M_{2}G} }}\wedge {\vec {\omega }}}$

et le vecteur accélération angulaire instantanée ${\displaystyle {\vec {\alpha }}}$ tel que les accélérations, qui se réduisent à leur composante tangentielle, des points matériel dans R' vaut :

${\displaystyle {\begin{aligned}{\vec {a'}}_{1}=\ &{\frac {\mathrm {d} }{\mathrm {d} t}}{\vec {v'}}_{1}\\=\ &{\frac {\mathrm {d} }{\mathrm {d} t}}({\overrightarrow {\mathrm {M_{1}G} }}\wedge {\vec {\omega }})\\=\ &{\frac {\mathrm {d} }{\mathrm {d} t}}({\overrightarrow {\mathrm {M_{1}G} }})\wedge {\vec {\omega }}+{\overrightarrow {\mathrm {M_{1}G} }}\wedge {\frac {\mathrm {d} }{\mathrm {d} t}}{\vec {\omega }}\\=\ &-{\vec {v'}}_{1}\wedge {\vec {\omega }}+{\overrightarrow {\mathrm {M_{1}G} }}\wedge {\vec {\alpha }}\\=\ &{\overrightarrow {\mathrm {M_{1}G} }}\wedge {\vec {\alpha }}\end{aligned}}}$

et de même

${\displaystyle {\vec {a'}}_{2}={\overrightarrow {\mathrm {M_{2}G} }}\wedge {\vec {\alpha }}}$.

Le moment de la force ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {R1} }}$ par rapport à G s'écrit :

${\displaystyle {\begin{aligned}{\vec {\mathcal {M}}}_{\mathrm {G} }({\vec {\mathrm {F} }}_{\mathrm {R1} })=\ &{\overrightarrow {\mathrm {GM} }}_{1}\wedge {\vec {\mathrm {F} }}_{\mathrm {R1} }\\=\ &m_{1}{\overrightarrow {\mathrm {GM} }}_{1}\wedge {\vec {a'}}_{1}\\=\ &m_{1}{\overrightarrow {\mathrm {GM} }}_{1}\wedge ({\overrightarrow {\mathrm {M_{1}G} }}\wedge {\vec {\alpha }})\\=\ &m_{1}\mathrm {GM} _{1}^{2}\alpha \sin({\overrightarrow {\mathrm {M_{1}G} }},{\vec {\alpha }})\cdot {\vec {u}}\\=\ &m_{1}\mathrm {GM} _{1}^{2}\sin({\overrightarrow {\mathrm {M_{1}M_{2}} }},{\vec {\alpha }})\alpha \cdot {\vec {u}}\end{aligned}}}$

où ${\displaystyle {\vec {u}}}$ est le vecteur directeur unitaire du vecteur moment. Si l'on note R₁ = GM₁ et R₂ = GM₂, on a :

${\displaystyle {\vec {\mathcal {M}}}_{\mathrm {G} }({\vec {\mathrm {F} }}_{\mathrm {R1} })=m_{1}\mathrm {R} _{1}^{2}\sin({\overrightarrow {\mathrm {M_{1}M_{2}} }},{\vec {\alpha }})\alpha \cdot {\vec {u}}}$

et de même

${\displaystyle {\vec {\mathcal {M}}}_{\mathrm {G} }({\vec {\mathrm {F} }}_{\mathrm {R2} })=m_{2}\mathrm {R} _{2}^{2}\sin({\overrightarrow {\mathrm {M_{1}M_{2}} }},{\vec {\alpha }})\alpha \cdot {\vec {u}}}$.

On appelle moment d'inertie par rapport à l'axe (Δ) = ${\displaystyle (\mathrm {G} ,{\vec {u}})}$ les quantités

J_Δ1 = m₁R₁²sin((M₁M₂), (Δ))

J_Δ2 = m₂R₂²sin((M₁M₂), (Δ))

et l'on a donc

${\displaystyle {\vec {\mathcal {M}}}_{\mathrm {G} }({\vec {\mathrm {F} }}_{\mathrm {R1} })=\mathrm {J} _{\Delta 1}\alpha \cdot {\vec {u}}}$

${\displaystyle {\vec {\mathcal {M}}}_{\mathrm {G} }({\vec {\mathrm {F} }}_{\mathrm {R2} })=\mathrm {J} _{\Delta 2}\alpha \cdot {\vec {u}}}$

Les deux vecteurs ont la même orientation, puisque ${\displaystyle {\overrightarrow {\mathrm {M_{1}G} }}}$ et ${\displaystyle {\overrightarrow {\mathrm {M_{2}G} }}}$ sont colinéaires et de sens inverse, et que ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {R1} }}$ et ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {R2} }}$ sont également colinéaires et de sens inverses.

Dans le référentiel R', le solide Σ est soumis à un couple total de moment

${\displaystyle {\vec {\mathcal {M}}}={\vec {\mathcal {M}}}_{\mathrm {G} }({\vec {\mathrm {F} }}_{\mathrm {R1} })+{\vec {\mathcal {M}}}_{\mathrm {G} }({\vec {\mathrm {F} }}_{\mathrm {R2} })=(\mathrm {J} _{\Delta 1}+\mathrm {J} _{\Delta 2})\alpha \cdot {\vec {u}}}$.

L'étude dynamique du système Σ des points matériels (M₁, m₁) et (M₂, m₂) peut se décomposer en deux parties :

• l'étude du point matériel (G, m) dans le référentiel galiléen R_g, soumis à la résultante des forces extérieurs à Σ ;
• l'étude des points matériels (M₁, m₁) et (M₂, m₂) dans le référentiel du centre de masse R' ;
• dans le cas où Σ est un solide indéformable, on peut définir le moment d'inertie J_Δ (en kg⋅m²) par rapport à l'axe d'accélération angulaire instantanée Δ, qui décrit la répartition de la masse de l'objet autour de l'axe, et qui fournit pour la rotation une équation similaire au principe fondamental de la dynamique en translation :

  ${\displaystyle {\vec {\mathcal {M}}}=\mathrm {J} _{\Delta }{\vec {\alpha }}}$.

Illustrons la simplification qu'apporte le centre d'inertie par deux cas particuliers.

Problème à trois corps : Soleil, Terre, Lune (l'échelle n'est pas respectée)

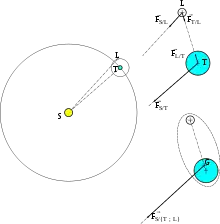
Le premier cas est celui du système {Soleil, Terre, Lune} (problème des trois corps) dans le référentiel héliocentrique : on peut considérer la Terre et la Lune comme deux points matériels,

• la Terre est soumise à l'attraction du Soleil, ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {S/T} }}$, et à l'attraction de la Lune ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {L/T} }}$ ;
• la Lune est soumise à l'attraction du Soleil, ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {S/L} }}$, et à l'attraction de la Terre ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {T/L} }}$.

Pour simplifier l'étude, on considère le système {Terre, Lune} comme s'il s'agissait d'un objet unique. La résultante des forces s'exerçant sur le centre d'inertie du système {Terre, Lune} vaut donc ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {S/T} }+{\vec {\mathrm {F} }}_{\mathrm {S/L} }}$.

Le second cas est celui de deux boules {1 ; 2} reliées par une barre rigide de masse négligeable, dans le référentiel terrestre.

• La boule 1 est soumise à son poids ${\displaystyle {\vec {\mathrm {P} }}_{1}}$ et à l'action de l'autre boule relayée par la barre ${\displaystyle {\vec {\mathrm {F} }}_{2/1}}$ ;
• la boule 2 est soumise à son poids ${\displaystyle {\vec {\mathrm {P} }}_{2}}$ et à l'action de l'autre boule relayée par la barre ${\displaystyle {\vec {\mathrm {F} }}_{1/2}}$.

Pour simplifier l'étude, on considère le système {1 ; 2} comme s'il s'agissait d'un objet unique. La résultante des actions s'exerçant sur le centre de gravité de {1 ; 2} se réduit également aux actions extérieures ${\displaystyle {\vec {\mathrm {P} }}_{1}+{\vec {\mathrm {P} }}_{2}}$.

Un solide continu Σ est défini par sa masse volumique ρ(M), où M est un point de Σ. On considère l'élément de volume infinitésimal dV autour de M ; il constitue un point matériel (M, ρ(M)dV). Le centre d'inertie de Σ se détermine en prenant le centre de masse mathématique des points (M, ρ(M)dV), qui est une version continue du barycentre :

${\displaystyle {\overrightarrow {\mathrm {OG} }}={\frac {1}{m}}\int _{\Sigma }\rho (\mathrm {M} ){\overrightarrow {\mathrm {OM} }}\cdot \mathrm {dV} }$

avec

${\displaystyle m=\int _{\Sigma }\rho (\mathrm {M} )\mathrm {dV} ~}$.

Le principe fondamental de la translation du point matériel (G, m) dans le référentiel galiléen R_g s'écrit

${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {ext} /\Sigma }=m{\vec {a}}_{\mathrm {G} }}$

où ${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {ext} /\Sigma }}$ est la résultante des forces extérieures s'exerçant sur Σ.