Automate quantique
En informatique quantique et en informatique théorique, un automate fini quantique est une généralisation des automates finis où un mot est accepté selon le résultat d'une certaine mesure. Il existe plusieurs modèles des automates finis quantiques ; le plus restrictif est celui des automates dits « measure-once » de Moore et Crutchfield 2000 ; un autre est celui des automates « measure-many » de Kondacs et Watrous 1997. Ces deux modèles sont très différents l'un de l’autre ; le modèle « measure-once » se rapproche plus de la théorie classique des automates finis. D'autres définitions, plus générales, ont été proposées, en généralisation des diverses variantes des automates, par exemple par Yakaryilmaz et Say 2011. Un des objectifs de l’étude des automates fini quantiques est l’étude des langages formels qu'ils acceptent ; un autre est d'étudier les problèmes de décidabilité pour ces classes d'automates et de langages.
Les automates finis quantiques sont similaires aux automates probabilistes, mais la classe des langages reconnus par automates quantiques est strictement contenue dans la classe des langages reconnus par automates probabilistes. Les automates finis quantiques peuvent aussi être vus comme une version quantique des sous-shifts de type fini, ou comme une variante quantique des chaînes de Markov. Les automates finis quantiques sont, à leur tour, des cas particuliers des automates finis dit géométriques ou des automates finis dit topologiques.
Un automate fini quantique opère sur des mots finis , dont les lettres sont dans un alphabet donné . Il attribue à chaque mot une probabilité; en fonction de cette probabilité, le mot est accepté ou rejeté par l'automate. Les langages acceptés par les automates finis quantique ne coïncident pas avec les langages rationnels acceptés par les automates finis, ni avec les langages stochastiques acceptés par les automates finis probabilistes.
Automate fini quantique MO
Des deux définitions d'automate fini quantique les plus usuelles, celle des automates « measure once » ou « MO » donnée par Moore et Crutchfield est la plus simple, et la plus proche des automates probabilistes plus traditionnels.
Définitions
Soit un entier positif. Un automate quantique au sens de Moore et Crutchfield, appelé automate « measure once » ou « MO », sur un alphabet est définie par les quatre données suivantes :
- un ensemble d'états. À chaque état est associé un élément noté d'un espace de Hilbert de dimension , en général , de sorte que forme une base orthonormée de . On suppose en général que est le -ème vecteur unité,
- un matrice unitaire d'ordre pour chaque lettre de . Cette matrice est la représentation d'un opérateur unitaire dans la base choisie.
- un vecteur d'ordre de norme , état quantique initial.
- une matrice de projection orthogonale d'ordre , correspondant à un projecteur orthogonal. Ce projecteur peut être remplacé parfois par un ensemble fini d'états terminaux, et la projection opère par projection sur ces états.
Les matrices et vecteurs sont à coefficients complexes.
Un état (quantique) est un vecteur qui se décompose sur la base et s'écrit, dans la notation bra-ket ou notation de Dirac usuelle en mécanique quantique, comme combinaison linéaire à coefficients complexes :
- ,
avec la condition additionnelle
- .
Cette écriture s'exprime en disant que est la superposition des états , le nombre est l'amplitude de l'état . Ainsi, chaque état quantique définit un certain « nuage » des états de : il est simultanément dans chacune des états, avec l'amplitude correspondante. Notamment, l'état quantique initial est aussi une combinaison linéaire des états de norme 1.
Pour un mot , le vecteur
est l'état quantique atteint après la lecture du mot ; comme il est représenté en vecteur colonne, les matrices s'appliquent en sens inverse. Dans les articles proches de la théorie des automates, on trouve la notation « duale », où les vecteurs d'états sont des vecteurs lignes, et l'écriture du produit des matrices correspond alors à la suite des lettres d'entrée lues[1].
La probabilité d'observation d'un état est le nombre , où est la matrice de projection donnée dans la définition. Une variante de définition consiste à donner un ensemble d'états terminaux. Alors la probabilité d'observation de est
- .
En écrivant
- ,
on voit que est une projection sur les états terminaux et que
de sorte que la probabilité d'observation s'écrit
- .
La probabilité d'acceptation d'un mot est par définition le nombre
- .
C'est donc la probabilité d'observation de l'état quantique obtenu après lecture du mot w. L'opération qui consiste à évaluer ce nombre est une mesure.
Le langage est accepté ou reconnu avec la probabilité est l'ensemble des mots tels que (acceptation par seuil strict) ou (acceptation par seuil large).
Variantes de notation et de modèle
Pour se rapprocher de notations employées par ailleurs en théorie des automates, l'état d'un mot est parfois noté . Pour un mot, on a alors
où est l'adjoint de l'état .
À la place de la notation matricielle, on rencontre aussi des fonctions de transition plus familières en théorie des automates. Une matrice est considérée comme une application de l'ensemble des états dans lui-même, avec et les coefficients du vecteur sont
- .
Enfin, on peut aussi travailler avec des nombres réels au lieu des nombres complexes. Le matrices unitaires sont alors des matrices orthogonales.
Fonction calculée par un automate quantique
Pour un automate quantique , notons la fonction définie par
qui associe à tout mot sa probabilité d'acceptation. C'est la fonction calculée par l’automate. Dans leur article[2], Moore et Crutchfield démontrent un certain nombre de propriétés de ces fonctions[3]. D'abord : La série formelle en variables non commutatives
est est une série formelle rationnelle (en). Les propriétés de clôture suivantes sont vraies : Soient et sont des fonctions calculées par des automates finies quantiques.
- (convexité) : est calculable par un automate fini quantique si .
- (intersection) : est calculée par un automate fini quantique.
- (complément): est calculée par un automate fini quantique.
- (morphisme inverse): Si est un morphisme, alors est calculable par automate fini quantique.
Lemme d'itération
Il existe aussi une sorte de lemme d'itération pour ces fonctions; il dit que pour tout et tout , il existe tel que pour tout et , on a .
Problèmes de décidabilité
Un certain nombre de résultats concerne la décidabilité de questions pour un automate fini quantique , avec la notation et pour une valeur de seuil donnée. Les questions suivantes sont indécidables :
- Existe-t-il un mot tel que ,
- Existe-t-il un mot tel que ,
- Existe-t-il un mot tel que .
En revanche, les questions suivantes sont décidables[4] :
- Existe-t-il un mot tel que ,
- Existe-t-il un mot tel que .
Tous ces problèmes sont en revanche indécidables pour les automates probabilistes.
Langages de points de coupure
Le langage reconnu par un automate quantique à seuil (respectivement à seuil strict ) est l’ensemble
- ou, respectivement, ,
où est la probabilité d'acceptation de dans l'automate . Le nombre est appelé un point de coupure (« cut point »).
Les problèmes de décider si le langage est vide ou si le langage est vide sont tous deux indécidables pour les automates probabilistes [5]. En revanche, pour les automates quantiques dans la définition de Moore et Crutchfield, le premier problème est indécidable alors que le deuxième est décidable.
Un point de coupure est dit isolé s'il existe un nombre tel que
pour tout mot ou, de manière équivalente, s'il existe un intervalle non vide autour de qui ne contient la probabilité d'acceptation d'aucun mot. Si un point de coupure est isolé, alors les langages et sont réguliers. De fait, on sait plus sur ces langages : ce sont des langages à groupes, c'est-à-dire des langages réguliers dont les monoïdes syntaxtiques sont des groupes finis[6] - [7].
Des questions liées sont :
- Étant donné et , est-ce que est isolé pour ?
- Étant donné , existe-t-il un point de coupure isolé pour ?
Ces questions sont décidables[8]. Il apparaît qu'un objet joue un rôle particulier dans cette étude, faite dans le cadre réel : c'est le groupe qui est la fermeture, pour la topologie euclidienne, du groupe (mathématiques) engendré par les matrices orthogonales d'un automate quantique. Ce groupe est compact. De plus, ce groupe est algébrique, ce qui signifie que sa clôture euclidienne est égale à sa clôture de Zariski. Le résultat principal qui permet la preuve est que la clôture de Zariski d'un groupe de matrices finiment engendré est effectivement calculable[8].
Exemple
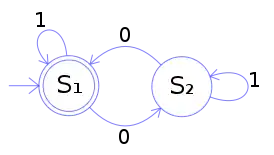
| 1 | 0 | |
| S1 | S1 | S2 |
| S2 | S2 | S1 |
Considérons l'automate fini déterministe à deux états donné ci-contre. Un état quantique est un vecteur qui s'écrit en notation bra-ket :
où les nombres complexes sont normalisés de sorte que . Les matrices de transition unitaires peuvent être simplement
- et .
Si l'on choisit comme état final, comme indiqué dans le diagramme, la matrice de projection est :
Si l'état initial est ou , le comportement de l'automate est exactement celui de l'automate fini usuel. En particulier, les mots qui sont acceptés le sont avec probabilité un, et le langage accepté a pour expression régulière l'expression : respectivement . Si en revanche et sont tous deux non nuls, le comportement est plus compliqué, et si de plus les matrices et ne sont pas aussi simples, on peut avoir d'encore d'autres résultats.
Automate fini quantique MM
Le modèle d'un automate quantique au sens de Kondacs et Watrous, appelé automate « measure many » ou « MM », diffère du modèle précédent : dans le modèle MO une mesure n'est effectuée qu'en fin de calcul. Dans le modèle MM considéré maintenant, une mesure est faite à chaque étape du calcul. Le principe de la physique quantique dit qu'une mesure est destructrice, et ce principe trouve son expression dans le formalisme proposé.
On a maintenant trois types d'états qui forment une partition de l'ensemble d'états[9]:
- des états d'acceptation
- des états de refus ou rejet,
- des états de continuation, , aussi appelés états neutres.
L'espace de Hilbert est décomposé en trois sous-espaces orthogonaux
correspondant aux trois types d'états . Pour chacun des trois ensembles d'états distingués, il y a une matrice de projection associée, notée et qui projette sur le sous-espace correspond. Elle est définie par
- ,
et de même pour les deux autres ensembles.
L'automate opère de la manière suivante : Après chaque lecture d'une lettre
- on mesure l'amplitude sur les états d'acceptation,
- on mesure l'amplitude sur les états de refus,
- on continue en ne conservant que les amplitudes des états de continuation.
La mesure consiste à vérifier si la projection est dans un sous-espace approprié. Après la lecture du mot, on a une probabilité d'acceptation et une probabilité de refus.
Plus précisément, soit l'état courant de l'automate. Soit
l'état de l’automate Après la lecture d'une lettre . Une mesure est réalisé en utilisant les opérateurs de projection, qui indiquent dans lequel des trois sous-espaces , ou se trouve l'image du vecteur. La probabilité est donnée par
pour l'espace des états acceptants, et de manière analogue pour les autres.
Pour une entrée , l'automate opère comme suit : en commençant avec le vecteur initial s, les vecteurs , sont mesurés tant que le résultat est dans l'espace de continuation. S'il est dans l'espace d'acceptation, le calcul s'arrête et le mot est accepté, s'il est dans l'espace de refus, le calcul s'arrête également, mais le mot est rejeté. On suppose que le mot est délimité par un marqueur de fin, et à la vue de ce marqueur, l'automate doit décider d'accepter ou de rejeter le mot, et il ne peut rester dans un état neutre. C'est donc un automate qui peut accepter ou rejeter un mot sans l'avoir lu dans sa totalité.
Formellement, l'automate définit une fonction sur les mots qui est
qui détermine la probabilité d'acceptation. Là aussi, l'expression « duale » se rencontre fréquemment.
Les mêmes questions que celles posées pour le modèle MO sont toutes indécidables pour le modèle MM.
Les langages reconnus par les automates MM avec un point de coupure isolé sont rationnels, mais ces automates ne sont pas assez puissants pour reconnaître tous les langages réguliers. Par exemple, le langage ne peut être reconnu par une automate MM avec point de coupure isolé[9].
Des variantes d'acceptation ont été étudiées pour les automates MM. Ainsi, des automates travaillant avec des « probabilités élevées » (par exemple au moins 7/9)[10], les langages acceptés sont reconnus aussi par des automates finis traditionnels réversibles, c'est-à-dire des automates dont les transformations définies par les lettres sont des fonctions partielles bijectives.
Les langages reconnus pas des automates MM ne sont pas fermés pour l'union, intersection ou les autres opérations booléennes usuelles.
Notes et références
- Par exemple Bertoni, Choffrut et d’Alessandro 2014.
- Moore et Crutchfield.
- Hirvensalo 2011.
- Blondel et al. 2005.
- (Rabin 1963).
- Brodsky et Pippenger 2002.
- Alex Brodsky et Nicholas Pippenger, « Characterizations of 1-Way Quantum Finite Automata », SIAM Journal of Computing, vol. 31, no 5, , p. 1456-1478 (DOI 10.1137/s0097539799353443).
- Derksen, Jeandel et Koiran 2005.
- Hirvensalo 2011, p. 162-163.
- La définition de l'acceptation par probabilité élevée est donnée dans A. Ambainis et R. Freivalds, « 1-way quantum finite automata: strengths, weaknesses and generalizations », Proceedings of the 39th FOCS, , p. 376–383 (DOI 10.1109/SFCS.1998.743469).
Bibliographie
- Michael O. Rabin, « Probabilistic Automata », Information and Control, vol. 6, no 3, , p. 230-245
- Alex Brodsky et Nicholas Pippenger, « Characterizations of 1-Way Quantum Finite Automata », SIAM Journal of Computing, vol. 31, no 5, , p. 1456-1478 (DOI 10.1137/s0097539799353443, arXiv http://xxx.lanl.gov/abs/quant-ph/9903014).
- Vincent D. Blondel, Emmanuel Jeandel, Pascal Koiran et Natacha Portier, « Decidable and undecidable problems about quantum automata », SIAM Journal of Computing, vol. 34, no 6, , p. 1464-1473 (DOI 10.1137/S0097539703425861)
- Harm Derksen, Emmanuel Jeandel et Pascal Koiran, « Quantum automata and algebraic groups », Journal of Symbolic Computation, vol. 39, nos 3-4, , p. 357-371 (DOI 10.1016/j.jsc.2004.11.008, lire en ligne).
- Alberto Bertoni, Christian Choffrut et Flavio d’Alessandro, « On the decidability of the intersection problem for quantum automata and context-free languages », International Journal on Foundations of Computer Science, vol. 25, no 8, , p. 1065-1081 (DOI 10.1142/s0129054114400243, arXiv https://arxiv.org/pdf/1303.2967v1.pdf).
- A. Yakaryilmaz et A.C.C. Say, « Unbounded-error quantum computation with small space bounds », Information and Computation, vol. 209, no 6, , p. 873-892
- Cristopher Moore et James P. Crutchfield, « Quantum automata and quantum grammars », Theoretical Computer Science, vol. 237, nos 1-2, , p. 275-306
- Attila Kondacs et John Watrous, « On the power of quantum finite state automata », FOCS’97: Proceedings of the 38th Annual Symposium on Foundations of Computer Science, , p. 66-75
- Andris Ambainis et Abuzer Yakaryilmaz, « Automata and Quantum Computing », sur arxiv,
- Mika Hirvensalo, Quantum Computing, Springer-Verlag, , 2e éd.
- Mika Hirvensalo, « Quantum Automata Theory – A Review », dans Werner Kuich et George Rahonis, Algebraic Foundations in Computer Science : Bozapalidis Festschrift, Springer-Verlag, coll. « Lecture Notes in Computer Science 7020 », (ISBN 978-3-642-24896-2, DOI 10.1007/978-3-642-24897-9), p. 146–167.
- (en) Luigi Accardi, « Quantum stochastic processes », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, (ISBN 978-1556080104, lire en ligne)






































































![{\displaystyle {\bigl [}\left[G({\mathcal {A}})\right]{\bigr ]}}](https://img.franco.wiki/i/9b6a9983b82ff3705d39e0bbccf72f6afe011d06.svg)
































