Application sous-linéaire

Soit $V$ un espace vectoriel sur ℝ. On dit qu'une application $s\,\colon \,V\to \mathbb {R} \cup \{+\infty \}$ est sous-linéaire[1] lorsque :

pour tous vecteurs $x$ et $y$ de $V$ , $s(x+y)\leq s(x)+s(y)$ (on dit que $s$ est sous-additive),
pour tout vecteur $x$ et tout $\lambda \geq 0$ , $s(\lambda x)=\lambda \,s(x)$ [2] (on dit que $s$ est positivement homogène[3]).

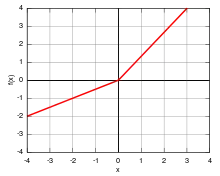
Illustration de la fonction f(x)={43xx≥012xx<0{\displaystyle f(x)={\begin{cases}{\tfrac {4}{3}}\,x&x\geq 0\\{\tfrac {1}{2}}\,x&x<0\end{cases}}}

Une application sous-linéaire est aussi dénommée pseudo-jauge en analyse fonctionnelle.

Les applications sous-linéaires sont convexes.

Comme exemples d'applications sous-linéaires, citons les semi-normes ou, plus généralement, toute jauge d'un convexe contenant l'origine. Une jauge est une pseudo-jauge à valeurs positives.

Notes et références

Cf. (en) Eric Schechter, Handbook of Analysis and Its Foundations, Academic Press, 1997 (lire en ligne), p. 313-314. Dans le cas particulier $V=\mathbb {R} ^{n}$ , on trouve une définition équivalente dans (en) Jean-Baptiste Hiriart-Urruty et Claude Lemaréchal, Fundamentals of Convex Analysis, Springer, coll. « Grundlehren Text Editions », 2004 (1^re éd. 2001) (ISBN 978-3-540-42205-1), p. 124 et dans (en) Jean-Baptiste Hiriart-Urruty et Claude Lemaréchal, Convex Analysis and Minimization Algorithms I: Fundamentals, Springer, coll. « Grundlehren Text Editions », 1993 (ISBN 3-540-56850-6), p. 198.
Pour $\lambda =0$ (avec la convention $0\times \infty =0$ ), cette condition implique $s(0)=0$ .
Ou « positivement homogène de degré 1 ».

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.