Analyse isentropique
L’analyse isentropique (sans changement d’entropie) en météorologie est une technique pour déterminer le trajet vertical et latéral que suivra une particule d’air lors d’un processus adiabatique dans l'atmosphère libre. Elle est basée sur l'étude de cartes météorologiques ou de coupes verticales des valeurs de température potentielle (ou de température potentielle équivalente) constantes[1] - [2]. La transformation de l'état de la particule d’air suivant ces iso-surfaces donne un bilan nul des échanges thermiques avec l'environnement. Ces analyses permettent aussi de connaître la stabilité de l’air si une particule d’air les croisent dans la verticale[3].
D'un point de vue synoptique, le transport par le vent des isolignes de température potentielle sur une carte météorologique permet de mieux repérer les fronts météorologiques, et les zones nuageuses associées, ainsi que la dynamique des masses d'air que l'analyse isobarique habituelle. De point de vue de la méso-échelle, elle permet de déterminer les couches de l'atmosphère où il y a potentiel de développement de nuages convectifs ou au contraire de nuages stratiformes, comme les nimbostratus[4].
Principe
Le mouvement des masses d’air à grande échelle, dite synoptique, implique un changement de volume et de température des particules d’air en mouvement selon un processus adiabatique où il n'y a idéalement aucun échange de chaleur avec l’environnement[5]. Une particule effectuant un tel processus conserve sa température potentielle et sa température potentielle équivalente car ces dernières représentent la température qu’aurait une particule d’air, quelle que soit son altitude, ramenée à une pression standard[5] :
Où :
- est la température du fluide (en kelvins) au niveau de pression
- la constante des gaz parfaits pour l'air (qui correspond à avec la constante universelle des gaz parfaits et la masse molaire de l'air)
- la chaleur massique à pression constante de l'air.
Et :
Les cartes de surfaces isentropiques représentent donc, pour une température équivalente donnée de la parcelle d'air, le niveau de pression où elle se trouve dans l’atmosphère. De façon équivalente, des cartes montrant la variation de pour un niveau de pression donnée sont également possible.
Le mouvement vertical sur une surface isentropique se fait par advection de pression, équivalent à l’advection de température sur une surface isobarique (carte de pression). Ainsi une advection de température à 850 hPa correspond à une zone de soulèvement et donc à un changement de hauteur de la surface isentropique.
Utilisation
Échelle synoptique
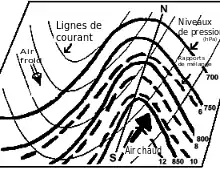
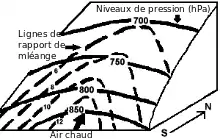
En règle générale dans la troposphère, la température diminue avec l’altitude. En faisant la transformation en température potentielle, cela veut dire que cette dernière diminue avec l’altitude[5]. De plus, les masses d’air sont plus chaude près de l’équateur et leur température diminue à niveau de pression équivalent en allant vers les pôles. Cela veut dire que la pente des surfaces isentropes (d’égal ) s'élève en allant vers les masses d’air plus froides[5]. En première approximation, un flux d’air chaud le long d’une surface isentrope va donc subir une ascension, alors qu’un flux d’air froid subira une descente. Les zones de variation de niveau de pression correspondent ainsi aux fronts météorologiques[5].
De même, l’analyse isentropique permet de suivre en trois dimensions le déplacement de l’humidité, contrairement à l’analyse isobarique qui ne permet que de voir ses variations à pression constante. Sur une carte en deux dimensions, une zone d’ascendance isentropique et de mouvement vertical d’humidité (lignes de rapport de mélange) correspond à une zone sur la carte isentropique où les vents (parallèle aux lignes de courant) croisent les lignes de et de rapport de mélange dont la valeur diminue[5]. Cela montre qu’une particule d’air suivant la surface isentrope s’élèvera graduellement vers l’altitude indiquée par le niveau de pression et que l’humidité à ce niveau augmentera. Ceci est donc associé avec la formation de précipitations le long d'un front chaud[5].
À l’inverse, une subsidence correspond à une zone où les vents croisent des valeurs de et de rapport de mélange en augmentation. Ceci indique que l’air provenant d’une altitude élevée (pression plus basse) descend vers une altitude plus basse et qu’elle apporte de l’air plus sec, donc derrière un front froid[5]. Naturellement, les processus diabatiques, où de la chaleur latente est échangée entre la masse d’air et l’environnement, comme le refroidissement nocturne ou le réchauffement diurne près de la surface terrestre, vont fausser les données isentropiques.
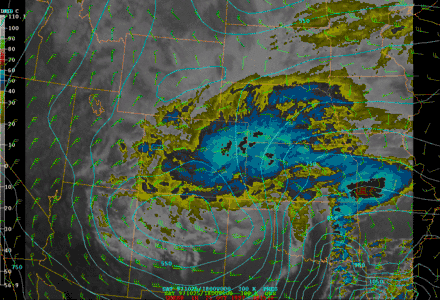
L'image en début d'article montre l'analyse isentropique lors d'une situation de blizzard au Colorado le . La photo des nuages prise par le satellite météorologique y est superposée. La position de la tête nuageuse correspond bien avec une advection des isotropes du sud vers le nord, alors que le dégagement du ciel, dans le quadrant sud-ouest, est bien corrélé avec une advection d'isotropes élevés vers le sud.
Échelle convective
Le concept de température potentielle permet également de comparer des parcelles d'air venant de différentes hauteurs dans la masse d'air[6]. Une coupe verticale à travers les surfaces isentropiques permet de voir la stratification de la température et donne une mesure de l'instabilité thermique de l'air[5] :
- Si diminue avec l'altitude, on a une masse d'air instable
- Si reste le même avec l'altitude, on a une masse d'air neutre
- Si augmente avec l'altitude, on a une masse d'air stable.
Une coupe verticale des données de température potentielle, observées ou prévues par un modèle de prévision numérique du temps, est donc équivalente à analyser un radiosondage sur un téphigramme ou un émagramme mais sur trois dimensions. La pente et la distance entre les isotropes indique jusqu'à quel point l'air est stable ou instable.
Avantages et inconvénients
- Avantages
Selon l’hypothèse de base, les mouvements de l’air à l’échelle synoptique est adiabatique sec. Cela implique que l’on se trouve dans l’atmosphère libre au-dessus de la couche limite où l’approximation géostrophique est relativement bonne. Il s’agit là d’une situation commune dans les latitudes moyennes et qui fonctionne bien avec le déplacement des dépressions frontales. L’analyse permet[5] :
- d’estimer directement la trajectoire des particules d’air à partir des données de pression et de vent rencontrées le long des surfaces isentropiques (cm/s) ;
- de mieux décrire le mouvement en trois dimensions de l’air dans la troposphère que les surface isobariques, et aussi bien le mouvement horizontal que ces dernières, si la vitesse verticale des particules est négligeable par rapport à celle horizontale ;
- la transformation de coordonnées isobariques en isentropes simplifie le calcul du tourbillon dans les équations primitives atmosphériques. Il devient le tourbillon potentiel isentrope.
- Inconvénients
D’un autre côté, l’analyse isentropique comporte certaines approximations qui comportent des désavantages[5] :
- Le flux synoptique n’est pas entièrement sec et/ou adiabatique, surtout dans la couche limite où il y a mélange vertical de l’air et échange de chaleur sensible avec le sol. La même chose peut être mentionnée dans les zones où il y a condensation(nuages, pluie et de nuages convectifs ) importante ;
- Lorsque la température potentielle diminue avec l’altitude, ce qui est courant près du sol lors de réchauffement diurne, une valeur de peut correspondre à deux altitudes ;
- Lorsque est presque constant avec l’altitude, ce qui est courant dans la couche limite où il y a homogénéisation par brassage de l’air, il peut être difficile de déterminer à quelle valeur isobarique se trouve la surface isentrope. Cependant, dans cette situation les autres paramètres (rapport de mélange, vent, etc.) sont en général uniformes avec l’altitude sur la surface isentrope.
- Contrairement aux surfaces à altitude constante, les surfaces isentropes peuvent couper le sol car elles sont calculées pour une pression standard de 1 000 hPa, et ont une pente plus raide que les surfaces isobariques ;
- Les cartes d’isotropes sont moins fréquentes que les cartes météorologiques habituelles car certaines données météorologique sont difficiles à transformer dans ces coordonnées ;
- Les valeurs standards des surfaces isentropes varient avec la saison, le thêta caractéristique des masses d’air en hiver (290-295 K) étant complètement différents de ceux en été par exemple (300 K et plus), alors que les surface isobariques standards (850, 500, 250 hPa) sont utilisables à l’année.
Notes et références
- Organisation météorologique mondiale, « Analyse isentropique », Glossaire de la météorologie, sur Eumetcal (consulté le )
- Service de traduction, « Analyse isentropique », sur Termium, Travaux publics et services gouvernementaux Canada (consulté le )
- Organisation météorologique mondiale, « Surface isentrope », Glossaire de la météorologie, sur Eumetcal (consulté le )
- (en) « Isentropic Analysis », COMET (consulté le )
- (en) James T. Moore, « Isentropic Analysis » [ppt], sur NOAA (consulté le )
- Organisation météorologique mondiale, « Analyse isentropique », sur Eumetcal (consulté le )










