Algorithme de Liu Hui pour π
L'algorithme de Liu Hui pour π a été inventé vers le IIIe siècle par Liu Hui, mathématicien chinois du royaume de Cao Wei. Avant lui, le rapport de la circonférence d'un cercle à son diamètre était souvent pris expérimentalement à trois en Chine, tandis que Zhang Heng (78 – 139) le prenait à 3,1724 (rapport du cercle céleste au diamètre de la terre, 92/29) ou encore à . Liu Hui , non satisfait de cette dernière valeur, a fait remarquer qu'elle était trop grande. Un autre mathématicien : Wang Fan (219 – 257) a proposé π ≈ 142/45 ≈ 3,156 [1]. Toutes ces valeurs empiriques de π sont exactes à deux chiffres (c'est-à-dire une décimale). Liu Hui a été le premier mathématicien chinois à fournir un algorithme rigoureux pour le calcul de π pour une précision quelconque. Le calcul personnel de Liu Hui à partir d'un polygone à 96 côtés a fourni une précision de cinq chiffres : π ≈ 3,1416 .
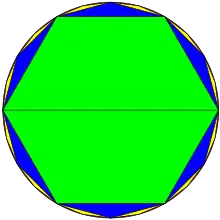
Liu Hui a remarqué dans son commentaire des Neuf chapitres sur l'art mathématique [2] que le rapport de la circonférence d'un hexagone inscrit au diamètre du cercle était de trois, donc π doit être supérieur à trois. Il a ensuite fourni une description détaillée étape par étape d'un algorithme itératif pour calculer π pour toute précision voulue basée sur des polygones bissecteurs ; il a estimé π entre 3,141024 et 3,142708 à partir d'un 96-gone ; il a suggéré que 3,14 était une approximation assez bonne et a exprimé π sous la forme 157/50 ; il a admis que ce nombre était un peu petit. Plus tard, il a inventé une méthode rapide pour l'améliorer et a obtenu π ≈ 3,1416 avec seulement un 96-gone, un niveau de précision comparable à celui d'un 1536-gone. Sa contribution la plus importante dans ce domaine a été son algorithme itératif simple de calcul de π.
Aire d'un cercle
Liu Hui a écrit :
« Multipliez un côté d'un hexagone par le rayon (de son cercle circonscrit), puis multipliez-le par trois, pour obtenir l'aire d'un dodécagone ; si nous coupons un hexagone en dodécagone, multipliez son côté par son rayon, puis multipliez à nouveau par six, nous obtenons l'aire d'un 24-gone ; plus nous coupons finement, plus la perte par rapport à l'aire du cercle est petite, donc en continuant coupe après coupe, l'aire du polygone résultant coïncidera et ne fera plus qu'un avec le cercle ; il n'y aura pas de perte. »
Apparemment, Liu Hui avait déjà maîtrisé le concept de limite [3]
De plus, Liu Hui a prouvé que l'aire d'un cercle est la moitié de sa circonférence multipliée par son rayon. Il a dit :
« Entre un polygone et un cercle, il y a un excès de rayon. Multipliez le rayon en excès par un côté du polygone. La zone résultante dépasse la limite du cercle. »
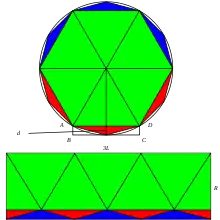
Dans le diagramme d = rayon excédentaire. En multipliant d par un côté, on obtient ABCD oblong qui dépasse la limite du cercle. Si un côté du polygone est petit (c'est-à-dire qu'il y a un très grand nombre de côtés), alors le rayon en excès sera petit, donc la zone en excès sera petite.
Comme dans le diagramme, lorsque N → ∞, d → 0 et ABCD → 0 .
« Multipliez le côté d'un polygone par son rayon, et l'aire double ; multipliez donc la moitié de la circonférence par le rayon pour obtenir l'aire du cercle. »
Lorsque N → ∞, la moitié du périmètre du N-gone s'approche d'un demi-cercle, donc une demi-circonférence d'un cercle multipliée par son rayon est égale à l'aire du cercle. Liu Hui n'a pas expliqué en détail cette déduction. Cependant, cela va de soi en utilisant le "principe du complément entrée-sortie" de Liu Hui qu'il a fourni ailleurs dans Les Neuf chapitres sur l'art mathématique : « Découpez une forme géométrique en parties, réarrangez les parties pour former une autre forme, la zone de les deux formes seront identiques. »
Ainsi, le réarrangement des six triangles verts, des trois triangles bleus et des trois triangles rouges en un rectangle de largeur vaut 3L, et la hauteur R montre que l'aire du dodécagone veut 3RL .
En général, la multiplication de la moitié de la circonférence d'un N-gone par son rayon donne l'aire d'un 2N-gone. Liu Hui a utilisé ce résultat de manière répétitive dans son algorithme pour π.
Inégalité de Liu Hui pour π

Liu Hui a prouvé un encadrement de π en considérant l'aire des polygones inscrits à N et 2N côtés.
Dans la figure, la zone jaune est celle d'un N-gone, d'aire , et la zone jaune plus la verte est celle d'un 2N-gone, d'aire . Par conséquent, la zone verte représente la différence entre celles du 2N-gone et du N-gone :
La zone rouge a même aire que la verte, et est donc aussi d'aire . Donc
- Zone jaune + zone verte + zone rouge =
Soit l'aire du disque. Alors
Si le rayon du cercle est pris égal à 1, alors nous avons l'inégalité de Liu Hui pour π :
Algorithme itératif
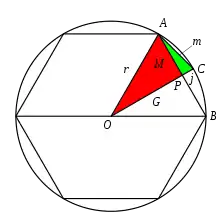
Liu Hui a commencé par un hexagone inscrit. Soit M la longueur d'un côté AB de l'hexagone, r est le rayon du cercle.
La droite (OPC) est la médiatrice de [AB] ; [AC] devient un côté du dodécagone (12-gone), soit m sa longueur . Soit j la longueur de [PC] et G la longueur de [OP].
APO, APC sont deux triangles rectangles. Liu Hui utilise plusieurs fois le théorème de Pythagore :
À partir de là, il existe une technique pour déterminer m à partir de M, qui donne la longueur du côté d'un polygone ayant le double d'arêtes. En partant d'un hexagone, Liu Hui a pu déterminer la longueur du côté d'un dodécagone à l'aide de cette formule. On itère pour déterminer la longueur du côté d'un tétraicosagone (24 côtés) compte tenu de la longueur du côté d'un dodécagone. On pourrait le faire récursivement autant de fois que nécessaire. Sachant déterminer l'aire de ces polygones, Liu Hui a pu alors approcher π.
Avec unités, il a obtenu
- aire d'un 96-gone
- aire d'un 192-gone
- Différence entre un 96-gone et un 48-gone :
- par l'inégalité de Liu Hui pour π :
- Puisque r = 10,
- donc:
-
Il n'a jamais pris π comme la moyenne de la borne inférieure 3,141024 et de la borne supérieure 3,142704. Au lieu de cela, il a suggéré que 3,14 était une approximation suffisamment bonne pour π, et l'a exprimé sous la forme d'une fraction 15750 ; il a souligné que ce nombre est légèrement inférieur à la valeur réelle de π.
Liu Hui a effectué son calcul par calcul de la tige et a exprimé ses résultats avec des fractions. Cependant, la nature itérative de l'algorithme de Liu Hui pour π est assez claire :
où m est la longueur d'un côté du polygone d'ordre suivant coupé en deux par M . Le même calcul est fait à plusieurs reprises, chaque étape ne nécessitant qu'une addition et une extraction de racine carrée.
Méthode rapide
Le calcul des racines carrées des nombres irrationnels n'était pas une tâche aisée au IIIe siècle avec les réglettes. Liu Hui a découvert un raccourci en comparant les différentiels d'aire des polygones et a découvert que la proportion de la différence d'aire des polygones d'ordre successif était d'environ 1/4[4].
Soit DN la différence des aires de N-gones et (N/2)-gones
Il a trouvé:
Ainsi:
Aire du cercle de rayon unitaire =
Dans lequel
C'est-à-dire que toutes les zones excédentaires ultérieures s'élèvent à un tiers de
- aire du cercle unitaire [2]
Liu Hui était assez satisfait de ce résultat car il avait obtenu le même résultat avec le calcul pour un 1536-gone, obtenant la surface d'un 3072-gone. Cela répond à quatre questions :
- Pourquoi s'est-il arrêté net à A192 dans la présentation de son algorithme ? Parce qu'il a découvert une méthode rapide pour améliorer la précision de π, obtenant le même résultat obtenu par un 1536-gone avec seulement un 96-gone. Après tout, le calcul des racines carrées n'était pas une tâche simple avec le calcul de la tige. Avec la méthode rapide, il lui suffisait d'effectuer une soustraction supplémentaire, une division supplémentaire (par 3) et une addition supplémentaire, au lieu de quatre extractions de racine carrée supplémentaires.
- Pourquoi a-t-il préféré calculer π en calculant les aires au lieu des circonférences des polygones successifs ? Car la méthode rapide nécessitait des informations sur la différence des aires des polygones successifs.
- Qui est le véritable auteur du paragraphe contenant le calcul de
- Ce célèbre paragraphe commençait par « Un conteneur en bronze de la dynastie Han dans l'entrepôt militaire de la dynastie Jin... ». De nombreux érudits, parmi lesquels Yoshio Mikami et Joseph Needham, pensaient que le paragraphe "conteneur en bronze de la dynastie Han" était l'œuvre de Liu Hui et non de Zu Chongzhi comme d'autres le pensaient, en raison de la forte corrélation des deux méthodes par le calcul de la surface, et parce que il n'y avait pas un seul mot mentionnant le résultat de Zu 3,1415926 < π < 3,1415927 obtenu par un 12288-gone.
Développements ultérieurs
Liu Hui a établi un algorithme solide pour le calcul de π avec n'importe quelle précision.
- Zu Chongzhi connaissait le travail de Liu Hui et a obtenu une plus grande précision en appliquant son algorithme à un 12288-gone.
- D'après la formule de Liu Hui pour un 2N-gone :
- Pour un 12288-gone inscrit dans un cercle de rayon unitaire :
- .
- De l'inégalité de Liu Hui pour π :
- Dans lequel
- .
- Donc
Tronqué à huit chiffres significatifs :
- .
C'est la fameuse inégalité de Zu Chongzhi pour π.
Zu Chongzhi a ensuite utilisé la formule d'interpolation de He Chengtian (何承天, 370-447) et a obtenu une fraction approximative : .
Cependant, cette valeur de π a disparu dans l'histoire chinoise pendant une longue période (par exemple le mathématicien de la dynastie Song Qin Jiushao a utilisé et ), jusqu'à ce que le mathématicien de la dynastie Yuan Zhao Yuqin travaille sur une variante de l'algorithme de Liu Hui, en coupant en deux un carré inscrit et obtient à nouveau [5].
Signification de l'algorithme de Liu Hui
L'algorithme π de Liu Hui a été l'une de ses contributions les plus importantes aux mathématiques chinoises anciennes. Il était basé sur le calcul de l'aire d'un N -gone, contrairement à l'algorithme d'Archimède basé sur la longueur de la circonférence du polygone. Avec cette méthode, Zu Chongzhi a obtenu le résultat à huit chiffres : 3,1415926 < π < 3,1415927, qui a détenu le record mondial de la valeur la plus précise de π pendant des siècles[6], jusqu'à ce que Madhava de Sangamagrama calcule 11 chiffres au XIVe siècle ou Jamshid al -Kashi calcule 16 chiffres en 1424 ; les meilleures approximations de π connues en Europe n'étaient précises qu'à 7 chiffres jusqu'à ce que Ludolph van Ceulen calcule 20 chiffres en 1596.
Voir aussi
- Méthode d'exhaustion (Ve siècle av. J.-C.)
- Algorithme de Zhao Youqin pour π (XIIIe – XIVe siècles)
- (en) Proof of Newton's Formula for Pi (XVIIe siècle)
Remarques
- La valeur correcte est de 0,2502009052
- 1
- Les valeurs correctes sont :
- 2
- La méthode rapide de Liu Hui était potentiellement capable de fournir presque le même résultat que l'algorithme classique avec un 12288-gone (3,141592516588) avec seulement un 96-gone.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Liu Hui's π algorithm » (voir la liste des auteurs).
- (en) Herman C. Schepler, « The Chronology of Pi », Mathematics Magazine, vol. 23, no 3, , p. 165–170 (ISSN 0025-570X).
- Needham, Volume 3, 66.
- D'abord remarqué par le mathématicien japonais Yoshio Mikami
- Yoshio Mikami: Ph.D. Dissertation 1932
- Yoshio Mikami said about the work of Zhao Yu Xin:"The sides and consequently the perimeters of these polygons are successively calculated in such a manner as followed by Liu Hui of old", p136, Development of Mathematics in China and Japan
- Robert Temple, The Genius of China, a refined value of pi, p144-145, (ISBN 1-85375-292-4)
BIbliographie
- (en) Joseph Needham, Science and Civilization in China : Volume 3, Mathematics and the Sciences of the Heavens and the Earth, Taipei, Caves Books, Ltd, .
- Wu Wenjun ed, History of Chinese Mathematics Vol III (in Chinese) (ISBN 7-303-04557-0)

















































