Algorithme de Hopcroft-Karp

Un sommet qui n'est pas extrémité d'une arête d'un couplage partiel ${\displaystyle M}$ est appelé un sommet libre. La notion de base sur laquelle repose l’algorithme est celle de chemin d'augmentation ; c'est un chemin qui commence en un sommet libre, qui finit en un sommet libre, qui alterne des arêtes hors du couplage et dans le couplage, et qui passe au plus une fois par chaque sommet, c'est-à-dire un chemin qui commence et finit en des sommets libres distincts, qui alterne des arêtes hors du couplage et dans le couplage, et qui passe au plus une fois par chaque arête. Il résulte de cette définition que, à l'exception de ses extrémités, tous les sommets d'un chemin d'augmentation, s'il y en a, sont de sommets non libres. Un chemin d'augmentation peut consister en une seule arête qui est hors du couplage et dont les deux extrémités sont des sommets libres. Plus généralement, un chemin d'augmentation a une arête de plus hors du couplage que dans le couplage.

Si ${\displaystyle M}$ est un couplage et ${\displaystyle P}$ est un chemin d'augmentation relativement à ${\displaystyle M}$, alors la différence symétrique ${\displaystyle M\oplus P}$ des deux ensembles d'arêtes constitue un couplage de taille ${\displaystyle |M|+1}$. Ainsi, en trouvant des chemins d'augmentation, on accroît par différence symétrique la taille d'un couplage.

Réciproquement, si un couplage ${\displaystyle M}$ n'est pas optimal, soit ${\displaystyle P}$ la différence symétrique ${\displaystyle P=M\oplus M^{*}}$ où ${\displaystyle M^{*}}$ est un couplage maximal. Comme ${\displaystyle M}$ et ${\displaystyle M^{*}}$ sont tous deux des couplages, chaque sommet a degré au plus 2 dans ${\displaystyle P}$ ; l'ensemble ${\displaystyle P}$ est donc constitué d'un ensemble de cycles disjoints, d'un ensemble de chemins avec autant d'arêtes dans que en dehors de ${\displaystyle M}$, de chemins d'augmentation pour ${\displaystyle M}$, et de chemins d'augmentation pour ${\displaystyle M^{*}}$ ; mais ce dernier cas est exclu puisque ${\displaystyle M^{*}}$ est maximal. Les cycles et les chemins qui ont autant d'arêtes dans et en dehors du couplage ne contribuent pas à la différence de taille entre ${\displaystyle M}$ et ${\displaystyle M^{*}}$, de sorte que cette différence est égale au nombre de chemins d'augmentation pour ${\displaystyle M}$ dans ${\displaystyle P}$. Ainsi, chaque fois qu'il existe un couplage ${\displaystyle M^{*}}$ plus grand que le couplage courant ${\displaystyle M}$, il doit aussi exister un chemin d'augmentation. Si un tel chemin d'augmentation ne peut être trouvé, l'algorithme par incrémentation termine puisque alors ${\displaystyle M}$ est optimal.

La notion de chemin d'augmentation dans un problème de couplage est étroitement liée à celle de chemin augmentant dans le problème de flot maximum ; ce sont des chemins où on peut augmenter la quantité de flot entre les extrémités. On peut transformer le problème du couplage biparti en une instance du problème du flot maximum, de sorte que les chemins alternants du problème de couplage deviennent des chemins augmentant dans le problème de flot[3]. En fait, une généralisation de la technique utilisée dans l'algorithme de Hopcroft-Karp à des réseaux de flots arbitraire est connue sous le nom d'algorithme de Dinic.

L'algorithme peut être décrit par le pseudo-code suivant :

Entrée: un graphe biparti ${\displaystyle G=(X\cup Y,E)}$

Sortie: un couplage ${\displaystyle M\subseteq E}$

${\displaystyle M\leftarrow \emptyset }$

répéter

${\displaystyle {\mathcal {P}}\leftarrow \{P_{1},P_{2},\dots ,P_{k}\}}$ ensemble maximal de chemins d'augmentation sans sommets communs et de longueur minimale

${\displaystyle M\leftarrow M\oplus (P_{1}\cup P_{2}\cup \dots \cup P_{k})}$

jusqu'à ${\displaystyle {\mathcal {P}}=\emptyset }$

Plus précisément, soient ${\displaystyle X}$ et ${\displaystyle Y}$ les deux ensembles dans la bipartition des sommets de ${\displaystyle G}$, et soit ${\displaystyle M}$ le couplage courant entre ${\displaystyle X}$ et ${\displaystyle Y}$. Une arête dans ${\displaystyle M}$ est dite couplée, les autres sont non couplées. L'algorithme opère par phases, et chaque phase consiste en les étapes suivantes :

• Un algorithme de parcours en largeur partitionne les sommets du graphe en couches. Les sommets libres de ${\displaystyle X}$ sont utilisés comme sommets de départ du parcours et forment la première couche de la partition. Au premier niveau du parcours il n'y a que des arêtes non couplées puisque par définition les sommets libres ne sont pas extrémités d'une arête couplée. Dans les étapes suivantes du parcours, le arêtes traversées doivent alternativement être couplées et non couplées. Plus précisément, lors de la recherche des successeurs d'un sommet de ${\displaystyle X}$, seules des arêtes non couplées peuvent être parcourues, alors qu'à partir d'un sommet de ${\displaystyle Y}$, seules des arêtes couplées peuvent être parcourues. La recherche se termine à la première couche ${\displaystyle k}$ où un ou plusieurs sommets libres de ${\displaystyle Y}$ sont atteints.

• Les sommets libres de ${\displaystyle Y}$ de la couche ${\displaystyle k}$ sont réunis en un ensemble ${\displaystyle F}$. Ainsi, un sommet ${\displaystyle v}$ est dans l'ensemble ${\displaystyle F}$ si et seulement s'il est l'extrémité d'un chemin d'augmentation de longueur minimale.

• L'algorithme détermine un ensemble maximal de chemins d'augmentation de longueur ${\displaystyle k}$ sans sommet commun[4]. L'ensemble de chemins disjoints est calculé par un algorithme de parcours en profondeur partant de l'ensemble ${\displaystyle F}$ vers les sommets libres dans ${\displaystyle X}$, en utilisant les couches du parcours en largeur pour guider le parcours : le parcours en profondeur ne peut suivre que des arêtes vers des sommets pas encore utilisés de la couche suivante, et les chemins dans l'arbre du parcours en profondeur doivent suivre alternativement des arêtes couplées et non couplées. Lorsqu'un chemin d'augmentation pour un des sommets de ${\displaystyle F}$ est trouvé, la recherche en profondeur redémarre à partir du sommet de départ suivant dans ${\displaystyle F}$. Tout sommet rencontré durant le parcours en profondeur est immédiatement marqué comme utilisé ; en effet, s'il n'y a pas de chemin de ce sommet vers ${\displaystyle X}$ à ce moment du parcours, alors le sommet ne pourra pas être utilisé non plus à un moment ultérieur du parcours. Ceci garanti que le temps du parcours en profondeur est en ${\displaystyle O(|E|)}$. On peut aussi opérer dans l'autre direction, des sommets libres de ${\displaystyle X}$ vers ceux de ${\displaystyle Y}$[5], qui est la variante utilisée dans le pseudo-code ci-dessous.
• Tous les chemins ainsi trouvés sont utilisés pour agrandir ${\displaystyle M}$.

L'algorithme se termine quand on ne trouve plus de chemin d'augmentation dans le parcours en largeur utilisée dans la première partie d'une phase.

Première phase.

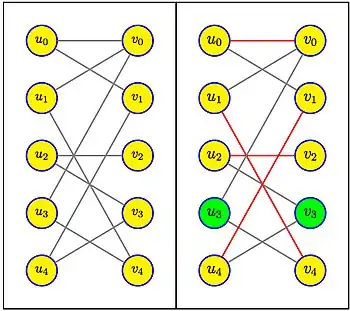
Le graphe biparti de l'exemple ci-contre a 5 sommets et 10 arêtes. Dans la partie gauche, avant la première phase, tous les sommets sont libres, le couplage est vide. Tous les chemins d'augmentation sont réduits à une seule arête entre un sommet de ${\displaystyle U}$ et un sommet de ${\displaystyle V}$. Un parcours en largeur sélectionne par exemple les arêtes ${\displaystyle (u_{0},v_{0})}$, ${\displaystyle (u_{1},v_{4})}$, ${\displaystyle (u_{2},v_{2})}$ et ${\displaystyle (u_{4},v_{1})}$ (en choisissant, pour chaque sommet de U éligible, le sommet de V de plus petit indice). Cet ensemble de chemins est bien maximal, tous ont même longueur 1, le couplage obtenu est de taille 4, et il reste deux sommets libres, ${\displaystyle u_{3}}$ et ${\displaystyle v_{3}}$.

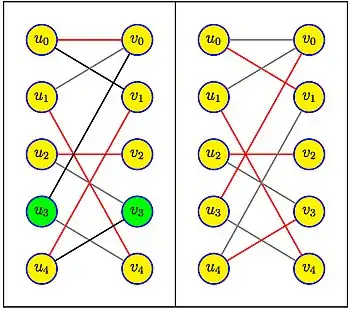
Dans la deuxième phase, il s'agit de trouver les chemins d'augmentation de longueur minimale, à partir du seul sommet libre de U (ou à partir du seul sommet libre de V). Le chemin indiqué ${\displaystyle (u_{3},v_{0},u_{0},v_{1},u_{4},v_{3})}$ en gras alterne des arêtes noires, hors couplage, et des arêtes rouges, dans le couplage. Il est de longueur 5. On voit bien qu'il n'existe pas de chemin de longueur 3 (les chemins sont toujours de longueur impaire), mais il y a un chemin de longueur 7, à savoir ${\displaystyle (u_{3},v_{4},u_{1},v0,u_{0},v_{1},u_{4},v_{3})}$. Le couplage résultant de la différence symétrique du couplage précédent avec le chemin de longueur 5 donne le couplage de taille 5 de l'exemple. Il est maximal parce qu'il n'y a plus aucun sommet libre.

Deuxième phase

Chaque phase consiste en un parcours en largeur suivi d'un parcours en profondeur. Chaque phase peut donc être réalisée en temps ${\displaystyle O(|E|)}$. Par conséquent, les ${\displaystyle |V|^{1/2}}$ premières phases, pour un graphe à ${\displaystyle |V|}$ sommets et ${\displaystyle |E|}$ arêtes, prennent un temps ${\displaystyle O(|E||V|^{1/2})}$.

On peut montrer[5] que chaque phase augmente d'au moins 1 la longueur du plus court chemin d'augmentation : dans une phase, on détermine un ensemble maximal de chemins d'augmentation d'une certaine longueur, donc tout autre chemin d'augmentation doit être plus long. Par conséquent, une fois les ${\displaystyle |V|^{1/2}}$ phases initiales de l'algorithme exécutées, le plus court chemin d'augmentation restant contient au moins ${\displaystyle |V|^{1/2}}$ arêtes. Or, la différence symétrique entre un couplage éventuellement optimal et le couplage partiel ${\displaystyle M}$ obtenu après les phases initiales de l’algorithme est une collection de chemins d'augmentation sans sommets communs, et de cycles alternants. Si chaque chemin dans cette collection a longueur au moins ${\displaystyle |V|^{1/2}}$, il y a au plus ${\displaystyle |V|^{1/2}}$ chemins dans cette collection, et la taille d'un couplage optimal diffère de la taille de ${\displaystyle M}$ par au plus ${\displaystyle |V|^{1/2}}$ arêtes. Comme chaque phase de l’algorithme augmente la taille du couplage d'au moins une unité, il y a au plus ${\displaystyle |V|^{1/2}}$ phases supplémentaires avant que l'algorithme termine .

Comme l'algorithme exécute au total au plus ${\displaystyle 2|V|^{1/2}}$ phases, il prend un temps en ${\displaystyle O(|E||V|^{1/2})}$ dans le pire des cas.

Dans de nombreux cas, le temps d'exécution peut être plus court que ce qu'indique cette analyse dans le pire des cas. Par exemple, l'analyse de la complexité en moyenne pour des graphes creux biparti aléatoires menée par Bast et al. 2006, améliorant des résultats antérieurs de Motwani 1994, montre qu'avec une grande probabilité, tous les couplages non optimaux ont des chemins d'augmentation de longueur logarithmique. Il en résulte que, pour ces graphes, l'algorithme de Hopcroft-Karp requiert ${\displaystyle O(\log |V|)}$ phases et un temps total en ${\displaystyle O(|E|\log |V|)}$.

Pour des graphes creux, l'algorithme de Hopcroft-Karp continue d'être l'algorithme le plus rapide connu dans le pire des cas, mais pour des graphes denses (pour lesquels ${\displaystyle |E|=\Omega (|V|^{2}}$) un algorithme ultérieur de Alt et al. 1991 donne une borne légèrement meilleure, à savoir ${\displaystyle O\left(|V|^{1.5}{\sqrt {|E|/\log |V|}}\right)}$. Leur algorithme commence par l'emploi de l'algorithme de poussage/réétiquetage et quand le couplage obtenu par cette méthode est près de l'optimum, bascule sur la méthode de Hopcroft-Karp.

Divers auteurs ont réalisé des comparaisons expérimentales de d’algorithmes de couplage de graphes bipartis. Leurs résultats, tels que résumés dans un rapport technique de Setubal 1996, tendent à montrer que la méthode de Hopcroft-Karp n'est pas aussi bonne en pratique qu'en théorie : d'autres méthodes sont plus rapides, en utilisant des parcours en largeur ou en profondeur plus simples pour la détermination des chemins d'augmentation, ou des techniques de poussage/réétiquetage.

La même façon de déterminer un ensemble maximal de chemins d'augmentation de longueur minimale pour trouver un couplage de taille maximale s'applique aussi dans des graphes non biparti, et pour la même raison les algorithmes basés sur cette idée demandent au plus ${\displaystyle O(|V|^{1/2})}$ phases. Toutefois, pour les graphes non biparti, trouver les chemins d'augmentation pour chacune des phases est plus difficile. En s'appuyant sur divers travaux antérieurs Micali et Vazirani 1980 ont montré comment implémenter chaque phase de l'algorithme en temps linéaire, ce qui finalement donne un algorithme pour le couplage dans les graphes non bipartis qui a la même borne de complexité que l'algorithme de Hopcroft-Karp pour les graphes bipartis. La technique de Micali-Vazirani est complexe, et leur article ne contient pas tout le détail des preuves ; une version qui se veut plus claire a été publiée ensuite par Peterson et Loui 1988, et d'autres méthodes ont été proposées par d'autres auteurs[6]. En 2012, Vazirani a fourni une démonstration simplifiée de l'algorithme de Micali-Vazirani algorithm[7].

Dans les pseudo-code ci-dessous, ${\displaystyle U}$ et ${\displaystyle V}$ forment la partition des sommets du graphe, et NIL est un somme spécial. Pour un sommet u de U, Pair_U[u] est NIL si u est libre, et sinon est égal à l'autre extrémité de l'arête à laquelle il est couplé. De même pour Pair_V[v].

function Hopcroft-Karp
    for each u in U
        Pair_U[u] = NIL
    for each v in V
        Pair_V[v] = NIL
    matching = 0
    while BFS() 
        for each u in U
            if Pair_U[u] == NIL
                if DFS(u) 
                    matching = matching + 1
    return matching

function BFS ()
    for each u in U
        if Pair_U[u] == NIL
            Dist[u] = 0
            Enqueue(Q,u)
        else
            Dist[u] = ∞
    Dist[NIL] = ∞
    while not Empty(Q)
        u = Dequeue(Q)
        if Dist[u] < Dist[NIL] 
            for each v in Adj[u]
                if Dist[ Pair_V[v] ] == ∞
                    Dist[ Pair_V[v] ] = Dist[u] + 1
                    Enqueue(Q,Pair_V[v])
    return Dist[NIL] != ∞

function DFS (u)
    if u != NIL
        for each v in Adj[u]
            if Dist[ Pair_V[v] ] == Dist[u] + 1
                if DFS(Pair_V[v]) 
                    Pair_V[v] = u
                    Pair_U[u] = v
                    return true
        Dist[u] = ∞
        return false
    return true

Dist[u] = ∞
return false

• [1993] Ravindra K. Ahuja, Thomas L. Magnanti et James B. Orlin, Network Flows: Theory, Algorithms and Applications, Prentice-Hall, 1993.
• [1991] Helmut Alt, Norbert Blum, Kurt Mehlhorn et Manfred Paul, « Computing a maximum cardinality matching in a bipartite graph in time ${\displaystyle \scriptstyle O\left(n^{1.5}{\sqrt {\frac {m}{\log n}}}\right)}$ », Information Processing Letters, vol. 37, n^o 4,‎ 1991, p. 237–240 (DOI 10.1016/0020-0190(91)90195-N).
• [2006] Holger Bast, Kurt Mehlhorn, Guido Schafer et Hisao Tamaki, « Matching algorithms are fast in sparse random graphs », Theory of Computing Systems, vol. 39, n^o 1,‎ 2006, p. 3–14 (DOI 10.1007/s00224-005-1254-y).
• Norbert Blum, « A Simplified Realization of the Hopcroft-Karp Approach to Maximum Matching in General Graphs », Tech. Rep. 85232-CS, Computer Science Department, Univ. of Bonn,‎ 2001 (lire en ligne).

• Jack Edmonds, « Paths, Trees and Flowers », Canadian J. Math, vol. 17,‎ 1965, p. 449–467 (DOI 10.4153/CJM-1965-045-4, MR 0177907).
• Harold N. Gabow et Robert E. Tarjan, « Faster scaling algorithms for general graph matching problems », Journal of the ACM, vol. 38, n^o 4,‎ 1991, p. 815–853 (DOI 10.1145/115234.115366).
• John E. Hopcroft et Richard M. Karp, « An n^5/2 algorithm for maximum matchings in bipartite graphs », SIAM Journal on Computing, vol. 2, n^o 4,‎ 1973, p. 225–231 (DOI 10.1137/0202019).
• Meena Mahajan, « Matchings in Graphs », The Institute of Mathematical Sciences, 13 janvier 2010 (consulté le 27 mars 2018).
• Silvio Micali et Vijay Vazirani, « An ${\displaystyle \scriptstyle O({\sqrt {|V|}}\cdot |E|)}$ algorithm for finding maximum matching in general graphs », Symposium on Foundations of Computer Science-Proc. 21st IEEE Symp. Foundations of Computer Science,‎ 1980, p. 17–27 (DOI 10.1109/SFCS.1980.12).
• Paul A. Peterson et Michael C. Loui, « The general maximum matching algorithm of Micali and Vazirani », Algorithmica, vol. 3, n^os 1-4,‎ 1988, p. 511–533 (DOI 10.1007/BF01762129).
• Rajeev Motwani, « Average-case analysis of algorithms for matchings and related problems », Journal of the ACM, vol. 41, n^o 6,‎ 1994, p. 1329-1356 (DOI 10.1145/195613.195663).

• João C. Setubal, « Sequential and parallel experimental results with bipartite matching algorithms », Tech. Rep. IC-96-09, Inst. of Computing, Univ. of Campinas,‎ 1996 (lire en ligne).
• Vijay Vazirani, « An Improved Definition of Blossoms and a Simpler Proof of the MV Matching Algorithm », CoRR abs/1210.4594,‎ 2012 (arXiv 1210.4594).

• Couplage biparti
• Algorithme hongrois
• Problème d'affectation
• Algorithme d'Edmonds-Karp de calcul de flot maximum

• Algorithme de Hopcroft-Karp sur Brilliant
• Algorithme de Hopcroft-Karp sur TUM