Algorithme hongrois
L'algorithme hongrois ou méthode hongroise, aussi appelé algorithme de Kuhn-Munkres, est un algorithme d'optimisation combinatoire, qui résout le problème d'affectation en temps polynomial. C'est donc un algorithme qui permet de trouver un couplage parfait de poids optimum (minimum ou maximum) dans un graphe biparti dont les arêtes sont valuées.
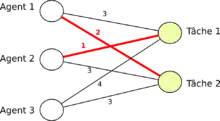
Algorithme
On peut présenter l'algorithme sous plusieurs formes. La première donnée est une présentation assez combinatoire utilisant des matrices, la seconde est une présentation dans le cadre de l'optimisation linéaire.
Description matricielle
Soit n projets et n équipes, et une matrice n×n d'entiers positifs, contenant le temps nécessaire à chaque équipe pour réaliser chaque tâche. On souhaite affecter chaque tâche à une équipe afin de minimiser le temps total de réalisation, c'est-à-dire la somme des temps pris pour chaque tâche.
On illustre ici l'algorithme avec une matrice de la forme suivante :
La version présentée ici correspond essentiellement à la version de Munkres en .
- Étape 0
Pour chaque ligne de la matrice, on soustrait à l'ensemble de la ligne la valeur minimale de celle-ci. La matrice a alors au moins un zéro par ligne. On répète la même opération sur les colonnes. On obtient alors un problème équivalent avec une matrice ayant au moins un zéro par ligne et par colonne.
| 0 | a2' | a3' | a4' |
| b1' | b2' | b3' | 0 |
| c1' | c2' | c3' | 0 |
| d1' | 0 | 0 | d4' |
Les étapes 1 et 2 vont permettre de sélectionner le maximum de zéros indépendants, c'est-à-dire sélectionner un seul zéro par ligne et par colonne. La procédure pour trouver le nombre maximum de zéros indépendants est explicitée par Munkres, là où Kuhn n'apportait pas de méthode constructive pour réaliser cette étape.
- Étape 1
On parcourt tous les zéros (non sélectionnés) et on sélectionne chaque zéro (en rouge ici) s'il n'est pas dans la même ligne ou colonne qu'un zéro déjà sélectionné.
| 0 | a2 | a3 | a4 |
| b1 | b2 | b3 | 0 |
| c1 | c2 | c3 | 0 |
| d1 | 0 | 0 | d4 |
Si l'on a sélectionné n zéros, alors on arrête l'algorithme.
Si l'on a sélectionné au moins un zéro supplémentaire au cours de cette étape, découvrez toutes les lignes et colonnes, retirez tous les primes (voir plus bas).
- Étape 2
- Couvrir chaque colonne ayant un zéro sélectionné.
| × | × | × | ||
| 0 | a2 | a3 | a4 | |
| b1 | b2 | b3 | 0 | |
| c1 | c2 | c3 | 0 | |
| d1 | 0 | 0 | d4 |
- Choisissez successivement un zéro non couvert, marquez-le d'un prime, puis
- S'il y a un zéro sélectionné sur sa ligne, alors découvrez la colonne de ce zéro-là et couvrez la ligne.
- S'il n'y a pas de zéro sélectionné sur sa ligne, alors on n'a pas sélectionné le nombre maximal de zéros indépendants, passez à l'étape 2'
× × 0 a2 a3 a4 b1 b2 b3 0 c1 c2 c3 0 d1 0 0' d4 ×
- S'il n'y a plus de zéro non couvert, alors d'après le théorème de König on a sélectionné le nombre maximal de zéros indépendants, et on a le nombre minimum de lignes et colonnes qui couvrent tous les zéros. Passez à l'étape 3.
- Étape 2'
On est dans le cas où l'on n'a pas sélectionné le nombre maximal de zéros indépendants.
Soit le seul 0' qui n'est pas couvert. Soit le zéro sélectionné sur la colonne de (qui existe sinon serait sélectionné à l'étape 1). Soit alors, , i pair, le 0' sur la ligne de qui existe nécessairement; et , i impair, le zéro sélectionné sur la colonne de s'il existe (sinon on arrête la suite).
La suite comprend alors un 0' de plus que de zéro sélectionné. On peut alors directement substituer ces 0' aux zéros sélectionnés de la suite. On a alors un ensemble avec un zéro indépendant de plus que précédemment. On retourne à l'étape 1, en gardant les nouveaux zéros sélectionnés, mais en effaçant les primes, et les couvertures de colonnes et lignes.
- Étape 3
Trouvez , la valeur minimum de la sous-matrice des éléments non couverts trouvée à l'étape 2. Il faut alors ajouter à toutes les lignes couvertes, et la retirer à toutes les colonnes non couvertes.
Retournez à l'étape 1, en conservant la sélection des zéros, la couverture les lignes et colonnes, et les primes.
Optimalité de la solution trouvée
On remarque que les seules modifications réalisées sur la matrice au cours de cet algorithme sont l'addition et la soustraction d'une valeur à l'ensemble d'une ligne ou d'une colonne. Une telle modification n’altère pas la ou les affectations optimales, mais uniquement le coût optimal. L'algorithme navigue donc entre des matrices correspondant à des problèmes équivalents.
De plus les valeurs de la matrice étant, et restant positives, l'algorithme ne peut s’arrêter, en étape 1, que sur une solution optimale pour la matrice modifiée (car de coût nul), et donc pour le problème original.
Démonstration du temps d’exécution polynomial
On peut montrer que l'algorithme, tel que présenté ici, s’arrête nécessairement en moins de opérations. Cependant, une amélioration proposée par Edmonds et Karp, (et Tomizawa indépendamment), permet de réduire le temps d’exécution à . On remarquera que n est en réalité la dimension de la matrice, et non la taille de l'entrée qui est elle de . On considère ici que l'addition, la soustraction, et la comparaison d'entiers sont des opérations de base et nécessitent . Cela dit, dans le cas contraire où l'on effectuerait les calculs sur des entiers longs (arithmétique multiprécision), cela ne changerait en rien l'aspect polynomial de l'algorithme par rapport à la taille de l'entrée du problème. En effet, la taille des entiers manipulés au fur et à mesure de l'algorithme reste forcément polynomiale, car seules les étapes 0 et 3 modifient la matrice et toutes deux ne peuvent faire augmenter la somme de tous les entiers de la matrice.
Complexité de l'algorithme original
Listons le nombre d'opérations nécessaires pour l’exécution de chacune des étapes.
- Étape 0 : . Pour chaque ligne et chaque colonne, n opérations pour calculer le minimum, puis n opérations pour le soustraire à chaque élément.
- Étape 1 : . En gardant en mémoire pour chaque ligne et chaque colonne un booléen disant si elle contient déjà un zéro sélectionné, il suffit de parcourir tous les éléments de la matrice, en vérifiant si c'est un zéro et si sa ligne et sa colonne contiennent un zéro sélectionné.
- Étape 2 : . Lister les zéros non couverts, et ajouter à cette liste les zéros nouvellement découverts lorsque l'on découvre une colonne. On suit alors la liste des zéros non couverts en vérifiant qu'ils le sont toujours. On couvre au plus n lignes, et, à chaque couverture de ligne, il est nécessaire de parcourir une ligne et une colonne, soit 2n cases.
- Étape 2' : .
- Étape 3 : .
Soit le nombre maximal de zéros indépendants dans la matrice au début de l’exécution de l'étape 3 pour la k-ième fois. On remarque facilement que, si , alors il n'y aura pas d'étape 2' entre la (k)ème et la (k+1)ème étape 3, car dans ce cas après la (k)ème étape 3 on a toujours sélectionné le nombre maximal de zéros indépendants. On peut de plus démontrer que, sous cette même hypothèse, au début de la (k+1)ème étape 3 on aura strictement plus de lignes couvertes qu'au début de la (k)ème étape 3. En effet, on remarque d'abord facilement que les zéros sélectionnés et primes sont conservés par l'étape 3. Étant donné que l'on a déjà sélectionné le nombre maximal de zéros indépendants après la (k)ème étape 3, on démontre aisément que les seules opérations qui peuvent être réalisées entre la (k)ème étape 3 et la (k+1)ème étape3 sont des couvertures de ligne. Il y aura au moins une couverture de ligne, car l'étape 3 fait apparaitre un zéro non couvert à l'endroit du minimum des éléments non couverts.
On en déduit qu'il ne peut y avoir que n successions d'étapes 1, 2 et 3 avant d'obtenir un zéro indépendant supplémentaire. L'algorithme se poursuit jusqu'à obtenir une matrice avec n zéros indépendants. Lors de l'obtention de x zéros indépendants supplémentaires à l'étape 3, au plus x étapes 2' se trouveront exécutées.
On en déduit que l'algorithme s’arrête, après l’exécution d'au plus des étapes présentées ci-dessus. Donc la complexité totale est .
On peut de plus démontrer que l'étape 3 ne peut augmenter la somme totale des entiers dans la matrice, et donc ne pose aucun problème en arithmétique multiprécision. En effet, après l'étape 2, et donc en début d'étape 3, le nombre de colonnes non couvertes est supérieur ou égal au nombre de lignes couvertes. Donc dans l'étape 3 on retire au moins autant de fois qu'on l'ajoute.
Description par l'optimisation linéaire
On présente maintenant l'algorithme depuis un autre point de vue. L'algorithme est le même, mais on utilise les résultats d'optimisation linéaire pour l'étudier[1]. On se place dans un graphe biparti dont les sommets sont divisés en deux groupes A et B de même cardinal, et où l'arête entre et est de poids .
Représentation par l'optimisation linéaire
Le programme d'optimisation linéaire en nombres entiers pour le problème du couplage parfait de poids minimum est le suivant, où la variable :
minimiser (minimiser le coût total) tel que pour tout (chaque sommet de est adjacent à une arête sélectionnée) et pour tout (chaque sommet de est adjacent à une arête sélectionnée) pour tout . (la variable vaut 1 si l'arête ab est sélectionnée, et 0 sinon)
On le relâche en un problème d'optimisation linéaire en nombres réels, en remplaçant par . Le dual de ce nouveau programme peut être écrit de la façon suivante :
maximiser tel que pour tout .
La condition d'optimalité dans ce cas est la suivante. Une solution x est optimale pour le primal (c.-à-d. pour le premier problème) s'il existe une solution (u,v) optimale pour le dual telle que :
Algorithme
Le principe de l'algorithme est de transformer peu à peu une solution (u,v) pour le dual, en respectant les contraintes, pour construire une solution primale satisfaisant les contraintes d'optimalité.
L'algorithme est le suivant :
- Initialisation :
- Boucle : Tant que le graphe G constitué des arêtes (a,b) telles que ne contient pas de couplage parfait, faire :
- Retourner un couplage parfait de G.
Correction et complexité
L'algorithme a une complexité en temps cubique[1].
Historique
Il a été proposé en 1955 par le mathématicien américain Harold Kuhn[3], qui l'a baptisé « méthode hongroise » parce qu'il s'appuyait sur des travaux antérieurs de deux mathématiciens hongrois : Dénes Kőnig et Jenő Egerváry (en)[4]. L'article a été publié dans la revue Naval Research Logistic Quarterly car le projet de recherche était financé par l'Office of Naval Research Logistics Branch[4]. James Munkres a revu l'algorithme en 1957, et a prouvé qu'il s'exécutait en temps polynomial[5].
En 2006, il a été découvert que le mathématicien allemand Charles Gustave Jacob Jacobi avait décrit l'algorithme dans un article posthume, au XIXe siècle[6].
L'algorithme est vu comme une des premières apparitions de l'idée de schéma primal-dual.
Liens avec d'autres algorithmes
L'algorithme d'Edmonds pour les couplages généralise l'algorithme hongrois et traite le problème du couplage maximum dans tous les graphes en temps polynomial.
Références
- (en) Ola Svensson (lecturer), Mateusz Golebiewski et Maciej Duleba (scribes), « Topics in Theoretical Computer Science, Lecture 5: Understanding and using Linear Programming », sur École polytechnique fédérale de Lausanne, .
- Un tel ensemble existe d'après le théorème de Hall.
- (en) « Harold W. Kuhn, in his celebrated paper entitled The Hungarian Method for the assignment problem, [Naval Research Logistic Quarterly, 2 (1955), pp. 83-97] described an algorithm for constructing a maximum weight perfect matching in a bipartite graph » dans András Frank (en), On Kuhn’s Hungarian Method – A tribute from Hungary
- (en) Harold W. Kuhn, « The Hungarian Method for the Assignment Problem: Introduction by Harold W. Kuhn », sur Tom Kelsey à l'Université de St Andrews.
- (en) James Munkres, Algorithms for the assignment and transportation Problem.
- (en) Silvano Martello, « Jenö Egerváry: from the origins of the Hungarian algorithm to satellite communication », Central European Journal of Operations Research, vol. 18, no 1, , p. 47-58 (lire en ligne).
































