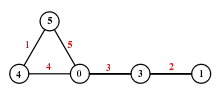
Étiquetage gracieux

En théorie des graphes, un étiquetage gracieux d'un graphe non orienté à m arêtes est un étiquetage de ses sommets par des entiers naturels distincts pris dans l'ensemble {0,...,m} qui a la propriété que les valeurs absolues des différences des étiquettes des extrémités des arêtes sont toutes distinctes et égales à 1,...,m ; elles identifient ainsi de manière unique les arêtes. Un graphe qui admet un étiquetage gracieux est un graphe gracieux[1] - [2].

Étiquetage gracieux. Les sommets sont étiquetés en noir, les arêtes en rouge.

Étiquetage gracieux d'une chaîne de 5 sommets.

Le terme « étiquetage gracieux » (en anglais « graceful labeling ») apparaît dans un article de Solomon W. Golomb[3] - [4] Le concept figure, sous le nom de « β-labeling » dans un article d'Alexander Rosa sur l’étiquetage de graphes[5].

Conjecture des arbres gracieux

Une des conjectures non résolues en théorie des graphes est la conjecture des arbres gracieux ou conjecture de Ringel-Kotzig, nommée ainsi d'après Gerhard Ringel and Anton Kotzig. Elle affirme :

Conjecture de Ringel-Kotzig — Tous les arbres sont gracieux.

La conjecture de Ringel-Kotzig est aussi connue sous le terme de « conjecture de l’étiquetage gracieux »[6]. Une version plus faible est la

Conjecture de Ringel — Le graphe complet $K_{2n+1}$ peut être décomposé en copies de tout arbre à $n$ arêtes.

Cette conjecture de Ringel a été démontrée pour des grandes valeurs de $n$ dans un article posté le 8 janvier 2020 par Richard Montgomery, Alexey Pokrovskiy et Benny Sudakov sur Arxiv[7]. Le résultat a fait l'objet d'un article dans Quanta Magazine[8] et dans Pour la Science[9]

Résultats partiels

De nombreux résultats partiels — positifs ou négatifs — concernent des classes particulières de graphes. Un catalogue est maintenu par Joseph A. Gallian[10] :

Un graphe eulérien avec m arêtes n'est pas gracieux si m ≡ 1 (mod 4) ou m ≡ 2 (mod 4)[5].
Un cycle C_n à n sommets est gracieux si et seulement si n ≡ 0 (mod 4) ou n ≡ 3 (mod 4)[5].
Toutes les chaînes et tous les graphes chenilles sont gracieux.
Tout graphe biparti complet est gracieux[1].
Les arbres à au plus 27 sommets sont gracieux[10] - [11]. Ce résultat est étendu en 2003 aux arbres à 29 sommets par Michael Horton dans sa thèse de bachelor[12]. Une autre extension, à 35 sommets, est annoncée en 2010 par Wenjie Fang[13].
Tout graphe roue, tout graphe grille est gracieux[10].
Tout hypercube est gracieux[14].
Les graphes simples avec au plus quatre sommets sont gracieux. Les seuls graphes à 5 sommets qui ne sont pas gracieux sont le 5-cycle (le pentagone); le graphe complet K₅; et le graphe graphe papillon[1].

Notes et références

(de)/(en) Cet article est partiellement ou en totalité issu des articles intitulés en allemand « Graziöse Beschriftung » (voir la liste des auteurs) et en anglais « Graceful labeling » (voir la liste des auteurs).

(en) Eric W. Weisstein, « Graceful graph », sur MathWorld
Virginia Vassilevska, « Coding and Graceful Labeling of trees », SURF 2001 PostScript
Solomon W. Golomb, « The Largest Graceful Subgraph of the Complete Graph », Amer. Math. Monthly, vol. 81,‎ 1974, p. 499-501.
Martin Gardner, Wheels, Life, and Other Mathematical Amusements, New York, W. H. Freeman, 1983, Ch. 15 : « Golomb's Graceful Graphs » p. 152-165.
A. Rosa, « On certain valuations of the vertices of a graph », dans Theory of Graphs (Internat. Sympos., Rome, 1966), New York, Gordon and Breach, 1967 (MR 0223271), p. 349-355.
C. Huang, Anton Kotzig et Alexander Rosa, « Further results on tree labellings », Utilitas Mathematica, vol. 21,‎ 1982, p. 31-48 (MR 668845).
« A proof of Ringel's Conjecture », 8 janvier 2020
Kevin Hartnett, « Rainbow Proof Shows Graphs Have Uniform Parts », sur https://www.quantamagazine.org, Quanta Magazine, 19 février 2020 (consulté le 8 juillet 2020).
« La conjecture de Ringel démontrée grâce à des coloriages de graphes », 30 juin 2020.
Joseph A. Joseph A. Gallian, « A dynamic survey of graph labeling », Electronic Journal of Combinatorics,‎ 1998-2016, Dynamic Survey #DS6: Dec 23, 2016 (MR = 1668059, lire en ligne).
R. E. L. Aldred et Brendan D. McKay, « Graceful and harmonious labellings of trees », Bulletin of the Institute of Combinatorics and its Applications, vol. 23,‎ 1998, p. 69-72 (MR 1621760).
Michael P. Horton, Graceful Trees : Statistics and Algorithms, Université de Tasmanie, 2003 (lire en ligne).
Wenjie Fang, « A Computational Approach to the Graceful Tree Conjecture », arxiv,‎ 2010 (arXiv 1003.3045).
Anton Kotzig, « Decompositions of complete graphs into isomorphic cubes », Journal of Combinatorial Theory, Series B, vol. 31, n^o 3,‎ 1981, p. 292-296 (DOI 10.1016/0095-8956(81)90031-9, MR 638285).

Bibliographie

Shalom Eliahou, « Le sudoku arboricole », Images des mathématiques : La recherche mathématique en mots et en images, CNRS, 21 décembre 2013 (consulté le 5 décembre 2017).
« Tous les arbres sont-ils gracieux ? », k a f e m a t h 2016-2017, 29 septembre 2016 (consulté le 5 décembre 2017).
Vasanti N. Bhat-Nayak et Ujwala N. Deshmukh, « Gracefulness of $C_{4t}\cup K_{1,4t-1}$ and $C_{4t+3}\cup K_{1,4t+2}$ », J. Ramanujan Math. Soc., vol. 11, n^o 2,‎ 1996, p. 187-190 (zbMATH 0867.05057).
Vasanti N. Bhat-Nayak et A. Selvam, « Gracefulness of $n$ -cone $C_{m}\vee K_{n}^{c}$ », Ars Combin., vol. 66,‎ 2003, p. 283–298 (MR 1961491).
(en) Eric W. Weisstein, « Graceful graph », sur MathWorld
Ping Zhang, A Kaleidoscopic view of graph colorings, Springer, coll. « SpringerBriefs in Mathematics », 2016, 157 p. (ISBN 978-3-319-30518-9, lire en ligne)

Étiquetage gracieux

Conjecture des arbres gracieux

Résultats partiels

Notes et références

Bibliographie

Articles liés