Voûte de pont en maçonnerie
La voûte est l’élément constitutif principal des ponts en maçonnerie, construits depuis la période romaine jusqu’à la fin du XIXe siècle, supportant toutes les charges appliquées sur l’ouvrage.
Terminologie
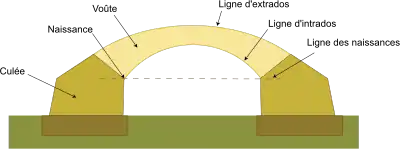
La voûte est délimitée géométriquement, dans un plan vertical, longitudinal par la ligne d’extrados, située à l’extérieur, et la ligne d’intrados, à l’intérieur. La ligne d’intrados est concave et peut présenter des points anguleux, à la clé en particulier, comme c’est le cas pour les voûtes ogivales. La ligne d’extrados peut, quant à elle, présenter des points d’inflexion, au droit des appuis souvent. Dans le plan transversal, les sections de la voûte sont rectangulaires[M 1].
Une voûte repose sur des extrémités, souvent appelées retombées, prolongées elles-mêmes par le corps des piles ou des culées sur lesquelles elle s’appuie[M 1].
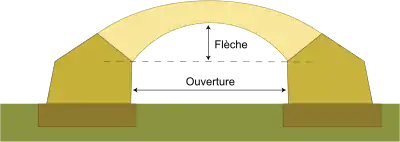
Les points d'intersection de la ligne d'intrados avec ces verticales s'appellent les naissances ou les reins. La distance qui sépare les culées s'appelle l'ouverture.
La ligne qui joint les naissances s'appelle ligne des naissances ou corde. Elle est presque toujours horizontale.
La distance verticale qui sépare la ligne d'intrados de la ligne des naissances, mesurée au milieu de celle-ci, s'appelle la flèche. Elle se représente par la lettre "f".
Caractéristiques des voûtes
Intrados voûte surmontée(image)
La forme des voûtes (ou arches) a varié selon les périodes. On distingue plusieurs types de voûtes selon la courbe affectée par la ligne d’intrados[1] - [2]:
- La voûte en plein cintre est constituée d’un demi-cercle complet,
- La voûte en arc de cercle ou segmentaire est constituée d’un demi-cercle incomplet,
- L’ogive est formée de deux arcs de cercle se coupant à la clef,
- L’anse de panier est formée d’un certain nombre d’arcs de cercle, avec des centres et des rayons différents et se raccordant aux points de passage de l’un à l’autre.
- L’ellipse est une courbe mathématique spécifique.
| Frise chronologique des caractéristiques des voûtes de ponts en maçonnerie | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Période romaine | Moyen Âge | Renaissance | XVIIe siècle XVIIIe siècle |
XIXe siècle | |||||||||||||||||
| intrados | Plein cintre | ||||||||||||||||||||
| Arc de cercle | |||||||||||||||||||||
| Ogivale | |||||||||||||||||||||
| Anse de panier | |||||||||||||||||||||
| Ellipse | |||||||||||||||||||||
| Plus grande portée | 32 m à Narni en Italie | 54,26 m Vieille-Brioude | 31,70 m Pont de Toulouse | 48,75 m Pont de Lavaur | 62 m Pont de Gournoir | ||||||||||||||||
| Surbaissement (arc de cercle) |
faible | faible | faible | 1/15,4 Nemours | 1/8 à 1/10 | ||||||||||||||||
| Appareil de la voûte | Pleine épaisseur | ||||||||||||||||||||
| Plusieurs rouleaux | |||||||||||||||||||||
| A anneaux superposés | |||||||||||||||||||||
| Par redents décalés | |||||||||||||||||||||
| Par appareils spécifiques | |||||||||||||||||||||
| Cintres | A fermes triangulaires | ||||||||||||||||||||
| retroussés | |||||||||||||||||||||
| A appuis multiples | |||||||||||||||||||||
| Rigides | |||||||||||||||||||||
Caractéristiques géométriques d’une voûte

Une voûte se définit par son ouverture et son surbaissement[M 2]. Si l'ouverture de la voûte est désignée par "2a" et la flèche par "f", le surbaissement de la voûte, désigné par la lettre , est le rapport flèche/ouverture soit :
La ligne d'intrados
Connaissant l'ouverture et la flèche, on peut déterminer la ligne d'intrados.
S'il s'agit d'un arc de cercle, on rappelle à ce sujet la formule bien connue:
S'il s'agit d'un arc de parabole ou d’un arc d'ellipse on peut construire la ligne d'intrados soit d'une façon précise, à partir de l'équation de la courbe, soit d’une façon approchée en traçant l'arc de cercle qui s'en rapproche le plus.
L'épaisseur de la voute
Il reste alors à déterminer l'épaisseur de la voûte. Celle-ci se définit à partir de certaines sections remarquables:
- celle du milieu ou section de clef,
- celles des naissances de la voûte, appelées sections des naissances,
- celles qui sont situées à mi-hauteur de la flèche, appelées sections aux reins.
Les caractéristiques d'un pont en maçonnerie ne peuvent se déterminer par les seules règles de la statique, mais seulement par approximations successives, à partir de dimensions choisies a priori que l'on vérifie; on dit que l'ouvrage est hyperstatique.
Puisque l'étude comporte un tâtonnement, on conçoit l'intérêt qui s'attache à choisir au départ, des dimensions aussi voisines que possible de celles qui seront en définitive retenues. On y parvient aisément grâce à la longue expérience que l'on a de ces ouvrages, qui a permis d'établir des formules empiriques donnant les épaisseurs à prévoir pour les sections remarquables des voûtes: clef, reins et naissances, ainsi que pour les culées et les piles.
Épaisseur à la clef
Plusieurs formules permettent de déterminer l'épaisseur à la clef (e0). Celles établies par Croizette-Desnoyers en 1885 sont :
| Type de voûte | Surbaissement (flèche/ouverture) |
Ponts-routes | Ponts-rails |
|---|---|---|---|
| Voûte en plein cintre[3] | e0 = 0,15 + 0,15 | e0 = 0,20 + 0,17 | |
| Voûte en arc de cercle[3] | e0 = 0,15 + 0,15 | e0 = 0,20 + 0,17 | |
| e0 = 0,15 + 0,14 | e0 = 0,20 + 0,16 | ||
| e0 = 0,15 + 0,13 | e0 = 0,20 + 0,15 | ||
| e0 = 0,15 + 0,12 | e0 = 0,20 + 0,14 | ||
| e0 = 0,15 + 0,11 | e0 = 0,20 + 0,13 | ||
| Voûte en arc d'ellipse[4] | e0 = 0,15 + 0,15 | e0 = 0,20 + 0,17 |
Épaisseur aux reins
A mi-hauteur de la flèche (voir illustration précédente)
Paul Séjourné conseille la formule : e1 = .e0 avec pour les valeurs suivantes :
| Type de voûte | Valeur de | Commentaires |
|---|---|---|
| Voûte en plein cintre | Cette valeur est un peu forte pour les voûtes de faible ouverture, inférieure à 8 m | |
| Voûte en arc d'ellipse | étant le surbaissement | |
| Voûte en arc de cercle | pour | |
| pour |
Épaisseur aux naissances
Pour les voûtes peu surbaissées (), il n'y a généralement pas lieu de connaître l'épaisseur aux naissances qui se confond pratiquement avec les reins, les culées commençant à partir de ceux-ci.
Pour les voûtes surbaissées (), on utilisera la formule suivante donnée par Paul Séjourné :
Notes et références
Notes
Ouvrages utilisés
- Eugène Degrand, Jean Resal, Ponts en maçonnerie, 1887, (voir dans la bibliographie)
- SETRA, Les ponts en maçonnerie, 1982, (voir dans la bibliographie)
- p. 11
- p. 37
- Marcel Prade, Les ponts, monuments historiques, 1986, (voir dans la bibliographie)
- Marcel Prade, Ponts et Viaducs au XIXe siècle, 1988, (voir dans la bibliographie)
Autres sources
- Marcel Prade - Les ponts monuments historiques – Éditions Brissaud – (ISBN 2903442819)
- Jean Mesqui, Répertoire des ponts routiers antérieurs à 1750. Tome 1, p. 26-29, SETRA, Direction des Routes, ministère de l'Équipement, Bagneux, 1975
- R est le rayon de l'intrados
- R est le rayon de l'arc de cercle qui aurait la même ouverture et le même surbaissement que l'arc d'ellipse
Annexes
Bibliographie
De très nombreux ouvrages traitant partiellement ou en totalité du sujet des ponts en maçonnerie ont été écrits. La liste ci-après, classée par ordre chronologique de parution, recense les plus significatifs et ceux qui ont servi de source à l'article.
Histoire
- Charles Duplomb, Histoire générale des ponts de Paris, Paris, Impr. Mersch, 1911.
- Éric Maré, The bridges of Britain, Londres, B.T. Batsford, 1954.
- Wolfgang W. Wurster et Joachim Ganzert, Eine Brücke bei Limyra in Lykien, Berlin, German Archaeological Institute, , 288–307 p. (ISSN 0003-8105)
- Mao Yisheng, Les ponts de Chine, Beijing (Chine), Éditions en langues étrangères, 1980.
- Sous la direction de Guy Grattesat, Ponts de France, Paris, Presses des Ponts et Chaussées, , 294 p. (ISBN 2-85978-030-0)
- Marcel Prade, Les Ponts, Monuments historiques, Poitiers, Brissaud, , 431 p. (ISBN 2-902170-54-8)
- Marcel Prade, Ponts et Viaducs au XIXe siècle, Poitiers, Brissaud, , 407 p. (ISBN 2-902170-59-9)
- Marcel Prade, Les grands ponts du Monde, Poitiers, Brissaud, , 312 p. (ISBN 2-902170-68-8)
- Marcel Prade, Ponts remarquables d'Europe : ouvrage illustré de 1000 photogr., dessins, et reprod., Poitiers, Brissaud, , 428 p. (ISBN 2-902170-65-3)
- Bernard Marrey, Les Ponts modernes : XXe siècle, Paris, Picard, , 280 p. (ISBN 2-7084-0484-9)
- Collectif, Troisième conférence internationale sur les ponts en arc, Paris, Presses des Ponts et Chaussées, , 360 p. (ISBN 978-2-85978-347-1, lire en ligne)
- Angia Sassi Perino et Giorgio Faraggiana (trad. de l'italien), Les Ponts, Paris, Gründ, , 184 p. (ISBN 978-2-7000-2640-5 et 2-7000-2640-3)
- Marc Giraud et Pascal Bejui, Paul Séjourné, génie des grands viaducs, La Roche Blanche (63) (France), La Régordane, , 208 p. (ISBN 978-2-906984-89-9)
XVIIe siècle
- Philippe de La Hire, Traité de Mécanique, Paris, (lire en ligne)
XVIIIe siècle
- Philippe de La Hire, Sur la construction des voûtes dans les édifices, Paris., Mémoires de l'Académie royale des sciences 69,, (lire en ligne)
- Antoine Parent, Essais et Recherches de Mathématiques et de Physique,, Paris.,
- Hubert Gautier, Dissertation sur l'épaisseur des culées de ponts, Paris, (lire en ligne)
- Bernard Forest de Bélidor, La Science des Ingénieurs dans la conduite des travaux de fortification et d'architecture civile, Paris., (lire en ligne)
- Couplet, De la poussée des voûtes. Histoire de l'Académie Royale des Sciences, 117, Paris., Paris, Académie royale des sciences, (lire en ligne)
- Amédée François Frézier, La théorie et la pratique de la coupe de pierres et des bois pour la construction des voûtes et autres parties des bâtiments civils et militaires, ou traité de stéréotomie à l'usage de l'architecture (3 vol.). ., Strasbourg et Paris, (lire en ligne)
- Charles Augustin Coulomb, Essai sur une application des règles de maximis et minimis à quelques problèmes de statique relatifs à l'architecture., Paris., Mémoires de Mathématique et de Physique, présentés à l'Académie royale des sciences par divers savants et lus dans ses Assemblées - Vol 7 - pp. 343-82 -, (lire en ligne)
XIXe siècle
- Joseph Balthasar Bérard, Statique des voûtes, Paris, Courcier, (lire en ligne)
- Jean-Baptiste Rondelet, Traité théorique et pratique de l'art de bâtir, Paris, l'auteur, 1802-1817.
- Jules Pillet, Traité de stabilité des constructions, Paris, Baudry et Cie, (lire en ligne)
- Pierre-Charles Lesage, Recueil de divers mémoires extraits de la Bibliothèque Impériale des Ponts et chaussées à l'usage de MM. les Ingénieurs ., Paris, (lire en ligne)
- Lamé et Clapeyron, Mémoire sur la stabilité de voûtes., Paris., Annales des Mines, 8, 789., (lire en ligne)
- Louis Bruyère, Études relatives à l'art des constructions, Paris, Bance, 1823-1828.
- Claude-Louis-Marie-Henri Navier, Résumé des leçons données à l'Ecole des Ponts et Chaussées, sur l'application de la mécanique à l'établissement des constructions et des machines, 2e édition, Paris., Paris, Carilian-Goeury, (lire en ligne)
- E. Méry, Équilibre des voûtes en berceau, pp. 50-70, Paris, Annales des ponts et chaussées,l, (lire en ligne)
- Joseph Cordier, Mémoire sur les travaux publics, Paris, Carilian-Gceury & V. Dalmont, 1841-1842.
- Emiland Gauthey, Traité de la construction des ponts, Liège (Belgique), Leduc, , 354 p.
- Tony, Fontenay, Prince Lubomirski, Construction des viaducs, ponts-aqueducs, ponts et ponceaux en maçonnerie, Paris, Carilian-Goeury & Victor Dalmont, 1852.
- J.V. Poncelet, Examen critique et historique des principales théories ou solutions concernant l'équilibre des voûtes., Paris, Comptes-rendus de l'Académie des Sciences. 35, 494, 531, 577, Tome XXXV. n° 17,
- Jules Carvallo, Étude sur la stabilité des voûtes, Paris, Carilian-Goeury, (lire en ligne)
- Herman, Scheffler (traduit par Fournié), Traité de la stabilité des constructions, Paris, Dunod, (lire en ligne)
- Alfred Durand-Claye, Stabilité des voutes en maçonnerie., Paris, Annales des Ponts et Chaussées pp. 63-96., (lire en ligne)
- Romain Morandière, Traité de la construction des ponts et viaducs, Paris, Dunod, 1874.
- Alfred Durand-Claye, Stabilité des voûtes et des arcs., Paris, Annales des Ponts et Chaussées pp. 416-440.,
- Philippe Croizette Desnoyers, Cours de construction des ponts, Vve Dunod, Paris., Paris, Dunod,
- Eugène Degrand et Jean Resal, Ponts en maçonnerie - tome 2 : Construction, Paris, Baudry et Cie, , 662 p.
XXe siècle
- Fernand de Dartein, Études sur les ponts en pierre remarquables par leur décoration antérieurs au XIXe siècle., Paris, Librairie polytechnique Beranger,
- Paul Séjourné, Grandes voûtes, Bourges, Impr. Vve Tardy, 1913-1916.
- Auguste Jouret, Paul Séjourné, Lyon, Impr. réunies, s.d. v. 1946.
- Encyclopédie pratique du bâtiment et des travaux publics : Tome I, Paris, Librairie Aristide Quillet, , 989 p.
- Encyclopédie pratique du bâtiment et des travaux publics : Tome II, Paris, Librairie Aristide Quillet, , 1035 p.
- Encyclopédie pratique du Bâtiment et des Travaux Publics : Tome III, Paris, Librairie Aristide Quillet, , 1016 p.
- Roger Valette, La construction des ponts., Paris, Dunod, 1958.
- Dragos Radenkovic, Théorie des charges limites. Séminaire de Plasticité, J. MANDEL Ed. P.S.T. Min. Air, n° 116, pp. 129-142.,
- Derrick Beckett, Bridges, Londres, Paul Hamlyn, 1969.
- O. Coussy et J. Salençon, Analyse de la stabilité des ouvrages en terre par le calcul à la rupture. Annales des Ponts et Chaussées, 4e trimestre, 1979 : pp. ?-35.,
- P. Rivière, Evaluation de la stabilité des ponts maçonnerie., Angers, Laboratoire Régional d'Angers. C.E.T.E. de l'Ouest. France.,
- Les ponts en maçonnerie, Bagneux, Ministère des Transports, Direction des routes, , 333 p.
- Guy Grattesat, Conception des ponts, Eyrolles,
- Anne Bernard-Gély, Jean-Armand Calgaro, Conception des ponts, Paris, Presses des Ponts et Chaussées, , 360 p. (ISBN 2-85978-215-X)
- Jean Salençon, De l'élasto-plasticité au calcul à la rupture, Paris, Éditions de l'école polytechnique, , 262 p. (ISBN 978-2-7302-0915-1 et 2-7302-0915-8, lire en ligne)
- Guide technique, Cours d'eau et ponts, Bagneux, SETRA, , 170 p. (ISBN 978-2-11-094626-3)
Articles connexes
Liens externes
- Structurae - Base de données et galerie internationale d'ouvrages d'art
.JPG.webp)



















