Tournoi (théorie des graphes)
En mathématiques, dans le cadre de la théorie des graphes, un tournoi est un graphe orienté obtenu en orientant chaque arête d'un graphe complet non orienté. On peut aussi le voir comme une orientation (en) d'un graphe complet, ou comme un graphe orienté où chaque paire de sommets est reliée par une arête orientée et une seule.
| Tournoi | |
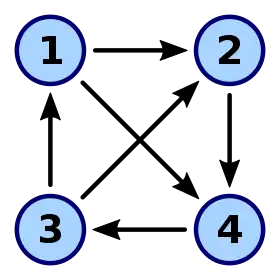 Un tournoi à 4 sommets. Ce tournoi est 1-paradoxal. Sa suite de scores est (1, 1, 2, 2). | |
| Nombre de sommets | |
|---|---|
| Nombre d'arêtes | |
Applications
De nombreuses propriétés importantes des tournois ont été explorées par H. G. Landau afin de modéliser des relations de dominations dans des groupes de poulets. Les applications actuelles des tournois concernent la théorie des systèmes électoraux ainsi que la théorie du choix en société, entre autres.
Le nom tournoi provient de l'interprétation de tels graphes comme le résultat d'un tournoi toutes rondes, dans lequel chaque participant rencontre chaque autre participant une fois et une seule, et dans lequel il n'y a pas égalité. Dans le graphe, les sommets correspondent aux participants et les arêtes correspondent aux résultats des parties jouées, l'arête allant du vainqueur au perdant. Si le participant bat le participant , on dit que domine , noté .
Chemins et circuits
Chaque tournoi sur un nombre fini de sommets contient un chemin hamiltonien, c'est-à-dire un chemin orienté passant par les sommets une fois et une seule. Ce résultat est dû à László Rédei en 1934[1].
Cette démonstration est constructive : elle fournit un algorithme permettant de trouver un chemin hamiltonien. Des algorithmes plus efficaces, qui ne supposent d'examiner qu'un nombre d'arêtes de l'ordre de , sont connus[2].
Cela a pour conséquence qu'un tournoi fortement connexe, c'est-à-dire tel qu'il existe un chemin entre n'importe quelle paire de sommets, possède un circuit hamiltonien, c'est-à-dire un cycle fermé et orienté passant par tous les sommets une fois et une seule (résultat dû à Paul Camion en 1959)[3].
Un résultat plus puissant est que tout tournoi fortement connexe est sommet-pancyclique : pour tout sommet et pour tout où est le nombre de sommets, il y a un circuit de longueur passant par [4].
Relations binaires
Un tournoi est parfois aussi défini comme une relation binaire entre et irréflexive dont la fermeture réflexive est totale et antisymétrique. Par définition, si domine , alors ne domine pas (antisymétrie); l'un des deux doit être vrai si est différent de (totalité). On peut noter l'antisymétrie de deux manières :
- où est la relation de domination.
Avec cette définition, on peut facilement vérifier que cette relation binaire est irréflexive :
- : Aucun élément ne peut être en relation avec lui-même. En effet, un participant ne peut pas se dominer lui-même.
On peut noter qu'un tournoi :
- Peut être transitif. Dans le cas où il ne l'est pas on dit que c'est un tournoi paradoxal.
- Ne peut pas être une relation totale car il n'est pas réflexif.
- Ne peut pas être une relation d'ordre (non stricte) car il n'est pas réflexif, mais c'est un ordre strict s'il n'est pas paradoxal.
- Ne peut pas être une relation d'équivalence car il n'est ni réflexif, ni symétrique.
Les relations binaires de tournoi ne sont pas des matrices de tournoi, on a donc :
- 1 si
- 0 si
- 0 si
Transitivité et tournois paradoxaux
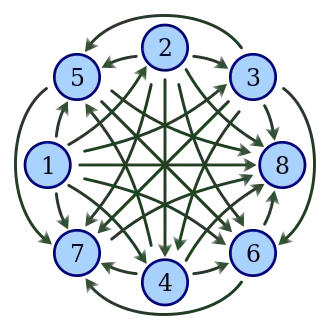
Dans les tournois de la vie réelle, on s'attend à ce que, si une personne domine une personne , et si domine à son tour une troisième personne , alors domine . Cela correspond à la transitivité de la relation binaire de domination.
Énoncé de façon formelle, cela donne la définition suivante :
On appelle transitif un tournoi dans lequel :
Étant donné un tournoi T à n sommets, les énoncés suivants sont équivalents :
- T est transitif ;
- T est acyclique ;
- T ne contient pas de circuit de longueur 3 ;
- La suite des scores de T (voir plus bas) est ;
- T possède exactement un chemin hamiltonien.
Un participant à un tournoi qui gagne toutes les parties est naturellement le gagnant du tournoi. Néanmoins, comme la figure tout en haut de cet article le montre, il est possible qu'un tel gagnant n'existe pas. Un tournoi lors duquel chaque participant perd au moins une partie est appelé tournoi 1-paradoxal.
De façon plus générale, un tournoi est appelé k-paradoxal si, pour tout sous-ensemble à éléments de , il existe un sommet dans tel que pour tous les sommets de .
Suite des scores et ensemble de scores
Dans un tournoi de la vie de tous les jours, s'il n'y a pas de vainqueur net (quelqu'un qui bat tous les autres), on peut essayer de départager les candidats en calculant leur score, c'est-à-dire le nombre de parties gagnées.
La suite des scores d'un tournoi est la suite ordonnée par ordre croissant des degrés sortants des sommets d'un tournoi.
L'ensemble des scores d'un tournoi est l'ensemble des degrés sortants des sommets du tournoi.
Le théorème de Landau (1953)[5] affirme qu'une suite d'entiers est une suite de scores si et seulement si :
- .
Par exemple, est bien une suite de scores, car :
- car ; car ; car
- car
De fait, cela correspond à la suite des scores du tournoi tout en haut de l'article.
En ce qui concerne les ensembles de scores, T. X. Yao a prouvé que n'importe quel ensemble non vide d'entiers positifs ou nuls est l'ensemble de scores d'un certain tournoi[6].
Matrice de tournoi
Il est naturel de noter les résultats d'un tournoi dans un tableau qui indique le résultat de chaque partie.
On appelle matrice de tournoi une matrice carrée dont le éléments valent :
- si
- si
- si .
Une matrice de tournoi est égale à l'opposé de sa transposée (elle est antisymétrique).
Notes et références
- (de) Lázló Rédei, « Ein kombinatorischer Satz », Acta Litteraria Szeged, vol. 7, , p. 39−43.
- (en) A. Bar-Noy et J. Naor, « Sorting, Minimal Feedback Sets and Hamilton Paths in Tournaments », SIAM Journal on Discrete Mathematics, vol. 3, no 1, , p. 7–20 (DOI 10.1137/0403002).
- Paul Camion, « Chemins et circuits hamiltoniens des graphes complets », C. R. Acad. Sci. Paris, vol. 249, , p. 2151−2152 (lire en ligne).
- J. W. Moon, « On subtournaments of a tournament », Canadian Mathematical Bulletin, vol. 9, no 3, , p. 297–301 (DOI 10.4153/CMB-1966-038-7, lire en ligne), Théorème 1.
- (en) H. G. Landau, « On dominance relations and the structure of animal societies. III. The condition for a score structure », Bulletin of Mathematical Biophysics, vol. 15, no 2, , p. 143–148 (DOI 10.1007/BF02476378).
- (en) T. X. Yao, « On Reid Conjecture Of Score Sets For Tournaments », Chinese Sci. Bull., vol. 34, , p. 804−808
Voir aussi
Sources
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Tournament (graph theory) » (voir la liste des auteurs).
- (en) Cet article reprend du contenu de la page Tournament sur PlanetMath sous licence CC_BT-SA.
Lien externe
(en) Eric W. Weisstein, « Tournament », sur MathWorld












![{\displaystyle i\in [0,n]}](https://img.franco.wiki/i/9242106e18dfff6aaf5c3150d134e96615dbe2fc.svg)







![{\displaystyle k\in [3,n]}](https://img.franco.wiki/i/4c22bb868affd20264a538ce97310ffe8377d535.svg)











































