Théorie de la similitude de Monin-Obukhov

La longueur de Monin-Obukhov Lest un paramètre ayant la dimension d'une longueur pour la couche de surface de la couche limite qui caractérise la contribution relative de l'énergie cinétique turbulente avec la production de flottabilité et de cisaillement. La longueur de Monin-Obukhov a été formulée à partir du critère de stabilité de Richardson pour la stabilité dynamique[4]. Il a été démontré que :

${\displaystyle L=-{\dfrac {u_{*}^{3}}{\kappa {\dfrac {g}{T}}{\dfrac {Q}{\rho c_{p}}}}}}$

où ${\displaystyle \kappa \approx 0.40}$ est la constante de von Kármán, ${\displaystyle u_{*}}$ est la vitesse de friction, Q est le flux de chaleur turbulent, et ${\displaystyle c_{p}}$ la capacité calorifique[4]. La température potentielle virtuelle ${\displaystyle \theta _{v}}$ est souvent utilisée au lieu de la température T pour tenir compte de l'influence de la pression et de l'humidité. Q peut être écrit comme un flux de tourbillons vertical :

${\displaystyle Q=\rho c_{p}{\overline {w'\theta _{v}'}}}$

où ${\displaystyle w'}$ et ${\displaystyle \theta _{v}'}$ sont respectivement les perturbations de la vitesse verticale et de la température potentielle virtuelle. Donc, la longueur d'Obukhov peut être définie comme suit[6] :

${\displaystyle L=-{\dfrac {u_{*}^{3}}{\kappa {\dfrac {g}{\overline {\theta _{v}}}}{\overline {w'\theta _{v}'}}}}}$

La longueur de Monin-Obukhov sert aussi de critère pour déterminer la stabilité statique de la couche de surface. Lorsque L < 0, l'atmosphère est statiquement instable tandis que lorsque L > 0, l'atmosphère est statiquement stable. La valeur de |1/L| indique l'écart par rapport à la stabilité statique neutre. On notera que dans ce cas ${\displaystyle L=\infty }$. Ainsi, lorsque |L| est petit, l'écart par rapport la stabilité neutre sera important (dans un sens ou dans l'autre). Cela veut dire que l'énergie cinétique sera dominante par rapport au cisaillement. La longueur de Monin-Obukhov est utilisée comme un facteur d'échelle pour la hauteur z.

La théorie de la similitude paramétrise les flux dans la couche de surface comme une fonction de la longueur réduite ζ = z/L. D'après le théorème de Vaschy-Buckingham de l'analyse dimensionnelle, deux groupes sans dimension peuvent être formés à partir du jeu de paramètres de base ${\displaystyle \{u_{*},g/{\overline {\theta _{v}}},\partial {\overline {u}}/\partial z,z,{\overline {w'\theta _{v}'}}\}}$,

${\displaystyle {\dfrac {\kappa z}{u_{*}}}{\dfrac {\partial {\overline {u}}}{\partial z}}}$, et ${\displaystyle \zeta ={\dfrac {z}{L}}}$

À partir de là, une fonction ${\displaystyle \varphi _{M}(\zeta )}$ peut être déterminée pour décrire empiriquement les relations entre les 2 quantités sans dimension. Cette fonction est appelée une fonction universelle. De même, ${\displaystyle \varphi _{H}(\zeta )}$ peut être définie par à partir du groupe sans dimension du profil de température moyenne. Le vent moyen et le prfil de température satisfont donc les relations suivantes[1] - [5] :

${\displaystyle {\dfrac {\partial {\overline {u}}}{\partial z}}={\dfrac {u_{*}}{\kappa z}}\varphi _{M}(\zeta )}$

${\displaystyle {\dfrac {\partial {\overline {\theta _{v}}}}{\partial z}}={\dfrac {\theta _{*}}{\kappa z}}\varphi _{H}(\zeta )}$

où ${\displaystyle \theta _{*}=-{\dfrac {\overline {w'\theta _{v}'}}{u_{*}}}}$ est la température dynamique caractéristique, ${\displaystyle \varphi _{M}}$ et ${\displaystyle \varphi _{H}}$ sont les fonctions universelles de la quantité de mouvement et de la chaleur. Les coefficients de diffusibilité des tourbillons pour les flux de quantité de mouvement et de chaleur sont définis comme suit :

${\displaystyle K_{M}=\kappa z{\dfrac {u_{*}}{\varphi _{M}(\zeta )}},\ K_{H}=\kappa z{\dfrac {u_{*}}{\varphi _{H}(\zeta )}}}$

${\displaystyle K_{M}}$ and ${\displaystyle K_{H}}$ peut être reliés au nombre de Prandtl turbulent ${\displaystyle Pr_{t}}$ comme suit :

${\displaystyle {\dfrac {K_{H}}{K_{M}}}={\dfrac {1}{Pr_{t}}}>1}$

En pratique, les fonctions universelles doivent être déterminées à partir de données expérimentales lorsque l'on utilise la théorie de la similitude. Bien que le choix des fonctions universelles n'est pas unique, certaines fonctions explicites ont été proposées et généralement acceptées car lissant bien les données expérimentales.

Fonctions universelles pour la théorie de la similitude de Monin-Obukhov

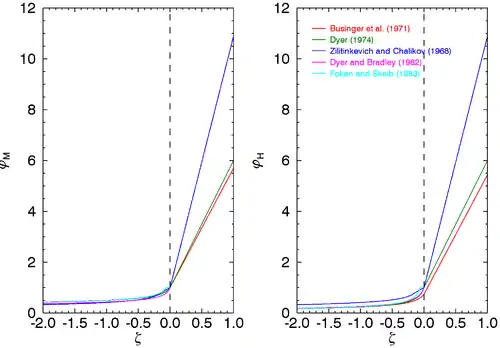
Plusieurs fonctions ont été proposées pour représenter les fonctions universelles de la théorie de la similitude. Puisque la longueur d'Obukhov est déterminée lorsque ${\displaystyle L{\Big (}{\dfrac {\partial Ri}{\partial z}}{\Big )}_{z=0}=1}$, la condition suivante doit être satisfaite par la fonction universelle choisie[1] :

${\displaystyle \varphi (0)=1}$

Une approximation au premier ordre pour le flux de moment est la suivante :

${\displaystyle \varphi _{M}(\zeta )=1+\beta \zeta }$

où ${\displaystyle \beta \approx 6}$[5]. Cependant, cette formule n'est utilisable que lorsque ${\displaystyle 0<\zeta <1}$. Lorsque ${\displaystyle \zeta <0}$, la relation devient :

${\displaystyle \varphi _{M}^{4}-\gamma \zeta \varphi _{M}^{3}=1}$

où γ est un coefficient qui doit être déterminé à partir de données expérimentales. Cette équation peut être approchée par ${\displaystyle \varphi _{M}=(1+\gamma \zeta )^{-1/4}}$ lorsque ${\displaystyle -2<\zeta <0}$.

Basée sur les résultats de l'expérience de 1968 au Kansas, les fonctions universelles suivantes ont été trouvées pour le vent moyen horizontal et la température potentielle virtuelle[7] :

${\displaystyle \varphi _{M}(\zeta )=(1-15\zeta )^{-1/4}\quad -2<\zeta <0}$

${\displaystyle \varphi _{M}(\zeta )=1+4.7\zeta \quad 0<\zeta <1}$

${\displaystyle \varphi _{H}(\zeta )=0.74(1-9\zeta )^{-1/2}\quad -2<\zeta <0}$

${\displaystyle \varphi _{H}(\zeta )=0.74+4.7\zeta \quad 0<\zeta <1}$

D'autres méthodes qui déterminent les fonctions universelles utilisant la relation entre ${\displaystyle \zeta }$ et ${\displaystyle Ri}$ ont été utilisées[8] - [9].

Pour les sous-couches ayant une rugosité importantes, comme les surfaces recouvertes de végétation ou les zones urbaines, les fonctions universelles doivent être modifiées pour tenir compte des effets de la rugosité[6].

Une pléthore d'expériences ont été effectuées pour valider la théorie de la similitude. Mesures in situ et simulations par ordinateur ont généralement démontré la validité de la théorie.

Mesures in situ

Un champ de blé typique du Kansas

L'expérience du Kansas de 1968 Kansas montrèrent un bon accord entre les mesures et les prévisions de la théorie de la similitude pour tout le spectre des paramètres de stabilité[7]. Un champ de blé plat dans le Kansas servait de site expérimental. Le vent avait été mesuré à l'aide d'anémomètres placés à différentes hauteurs le long d'une tour de 32 m de hauteur. Le profil de températures avait été mesuré de la même manière. Les résultats expérimentaux montrèrent que le rapport entre la diffusibilité des tourbillons de chaleur et de quantité de mouvement étaient de l'ordre de 1.35 en conditions de stabilité neutre. Une expérience similaire fut effectuée au nord du Minnesota en 1973. Utilisa à la fois des mesures au sol et par radiosonde de la couche de surface et validèrent plus avant les prévisions de la théorie de la similitude[10].

La théorie de la similitude bien que vérifiée expérimentalement pour la couche de surface, est essentiellement une formulation empirique basée sur la clôture au premier ordre de la turbulence. Les erreurs associées aux fonctions universelles sont typiquement de l'ordre de 10%~20%. Lorsque l'on applique ces formules pour des surfaces recouvertes de végétation ou des terrains complexes, les différences peuvent être importantes. Comme les fonctions universelles sont en général déterminées lorsque le temps est sec, la validité de la théorie de la similitude n'a pas été vérifiée suffisamment lorsque le temps est humide.

Un paramètre de base de la théorie de la similitude est la production de flottabilité ${\displaystyle {\dfrac {gQ}{T}}}$. Il est argumenté qu'avec un tel jeu de paramètres, le changement d'échelle est appliqué aux caractéristiques globales de l'écoulement, tandis qu'une relation de similitude spécifique aux tourbillons utilise préférentiellement le taux de dissipation d'énergie ε₀[12]. Cette approche permet d'expliquer les anomalies de la théorie de la similitude de Monin-Obukhov mais devient non locale en ce qui concerne les modèles et les expériences.

• Longueur de Monin-Obukhov
• Profil logarithmique des vitesses

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Monin–Obukhov similarity theory » (voir la liste des auteurs).