Taux zéro-coupon

Seul un ensemble de taux zéro-coupon permet de calculer des coefficients d'actualisation cohérents. Tout autre mode de raisonnement introduit des biais dans le calcul.

Si, pour les besoins des particuliers ou des PME, la notion de taux actuariel suffit généralement, celle-ci est tout à fait insuffisante pour les gestionnaires de fonds et les professionnels des marchés financiers. Ceux-ci utilisent, pour actualiser les flux financiers d'un instrument, des taux zéro-coupon différents, correspondant aux dates de chacun des flux, plutôt que d'appliquer un taux actuariel global, sorte de taux moyen ne tenant pas compte de la forme de la courbe des taux.

Il peut exister deux grandes catégories de courbes des taux zéro-coupon :

• celles qui sont constatées, sur le marché des strips, c’est-à-dire des emprunts d'État démembrés ;
• celles qui sont calculées.

Néanmoins, comme seulement environ 10 % des obligations assimilables du Trésor et 5 % des Bunds qui peuvent l'être sont effectivement démembrés, les instruments susceptibles de la composer ne sont pas assez liquides pour qu'on puisse disposer d'une courbe cohérente. Seules les courbes calculées, et qui dans le cas des emprunts d'État ne sont que des courbes théoriques, ont véritablement un sens.

Par définition, on a, pour une période séparant une date d d'une date D plus éloignée :

${\displaystyle CA(d,D)={\frac {1}{(1+Z(d,D))^{(D-d)}}}}$

où :

• CA(d, D) est le coefficient d'actualisation à la date d applicable à la date D;
• Z(d, D) est le taux zéro-coupon de d à D.

Si l'on dispose des coefficients d'actualisation, on disposera donc d'une courbe zéro-coupon et inversement.

On utilise nécessairement un processus itératif. En effet, jusqu'à un an, tous les taux sont nécessairement zéro-coupon. Par exemple, un taux actuariel, donc zéro-coupon, à un an plus un taux actuariel à deux ans permettent de trouver le taux zéro-coupon à deux ans, et ainsi de suite.

Ce processus est traditionnellement appelé en anglais bootstrapping, car jusqu'aux années 1990 les données des marchés de taux d'intérêt comportaient souvent des « trous » sur certaines durées, que l'explosion de l'endettement des États a depuis largement comblés, et sur lesquels il fallait interpoler. Cette expression fait référence aux aventures du baron de Münchhausen, lequel est censé s'être sorti d'un marécage où il était embourbé rien qu'en se tirant par les bottes et se propulsant ainsi dans les airs. Les bootstraps sont les anneaux, en cuir ou en tissu, cousus sur le rebord des bottes et dans lesquels on passe les doigts pour s'aider à les enfiler.

Il est particulièrement aisé de déterminer une courbe de taux zéro-coupon à partir d'une courbe de taux actuariels au pair, c'est-à-dire une dont les taux nominaux sont égaux aux taux actuariels, comme une courbe de swaps.

Si on note

${\displaystyle S_{n}=\sum _{i=1}^{n}CA(0,D_{i})}$

et ${\displaystyle T_{n}}$ le taux actuariel applicable à l'échéance n,

on a alors :

T_n . S_n + CA(0,D_n) = 1

Le problème principal, dans le calcul de taux zéro-coupon sur des emprunts d'État, vient de ce qu'ils ne sont pas véritablement fongibles, à la différence des swaps, que leur courbe de taux est donc irrégulière et qu'on doit donc procéder à un calcul statistique qui ne peut être entièrement automatisé. Il faut en effet procéder à des choix : quelles irrégularités garder, car elles sont structurelles, quelles autres faut-il corriger, etc?

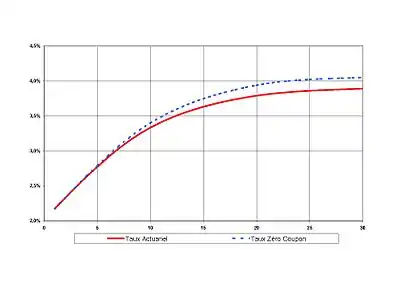
Elle ne coïncide avec la courbe des taux actuariels sous-jacente que dans un seul cas, d'ailleurs fort improbable, celui ou la courbe actuarielle serait une droite horizontale.

Dans tous les autres cas, la courbe zéro-coupon va amplifier les caractéristiques de la courbe actuarielle dont elle est issue :

• une courbe croissante, comme sur le graphe ci-dessus, donnera lieu à une courbe zéro-coupon
  • située au-dessus d'elle
  • et encore plus croissante;
• une courbe décroissante (l'expression consacrée est : inversée) donnera lieu à une courbe zéro-coupon
  • située en dessous d'elle
  • et encore plus décroissante.