Tétradécagone

Un tétradécagone ou tétrakaidécagone ou quadridécagone est un polygone à 14 sommets, donc 14 côtés et 77 diagonales.

La somme des angles internes de tout tétradécagone non croisé vaut 2 160 degrés.

Un tétradécagone régulier est un tétradécagone dont les 14 côtés ont la même longueur et dont les 14 angles internes ont même mesure. Il y en a trois : deux étoilés (les tétradécagrammes notés {14/3} et {14/5}) et un convexe (noté {14}). C'est de ce dernier qu'il s'agit lorsqu'on dit « le tétradécagone régulier ».

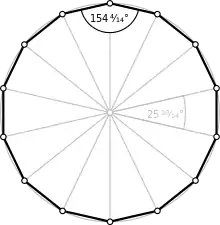
« Le » tétradécagone régulier (convexe) et ses angles remarquables.

Les deux tétradécagones réguliers étoilés
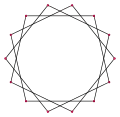{14/3}
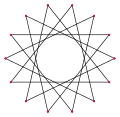{14/5}

Caractéristiques du tétradécagone régulier

Si $a$ est la longueur d'une arête :

le périmètre vaut $P = 14 a$ ;
l'aire vaut $A = (7 a 2 /2) cot (π/14)$ ;
l'apothème vaut $H = 2 A / P = (a /2) cot(π/14)$ ;
le rayon vaut $R={\frac {H}{\cos({\frac {\pi }{14}})}}={\frac {a}{2\sin({\frac {\pi }{14}})}}~;$
chacun des 14 angles au centre mesure 360°/14, soit environ 25,714° ;
chaque angle interne mesure 2 160°/14, soit environ 154,286°.

Voir aussi

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.