Square One
Le Square One est un casse-tête équivalent du Rubik's Cube. Il a été inventé par Karel Hršel et Vojtěch Kopský en 1990. Sa spécificité est qu'il prend, contrairement au cube classique, des centaines de formes différentes. Ainsi certains mouvements ne sont parfois plus possibles, ce qui en fait un puzzle des plus difficiles de la famille des Rubik's.
casse-tête

| Auteur |
Karel Hršel Vojtěch Kopský |
|---|---|
| Date de 1re édition | 1990 |
| Mécanisme | Rubik's Cube |
| Joueur(s) | 1 |
| habileté physique | réflexion décision | générateur de hasard | info. compl. et parfaite |

Histoire
Le Square One, de son nom entier "Back to Square One", et avec son nom alternatif "Cube 21", fut inventé par Karel Hršel et Vojtěch Kopský vers 1990. Son brevet tchécoslovaque fut créé le , et fut approuvé le sous le numéro de brevet CS 277266 B6. Le , il fut breveté aux États-Unis sous le numéro de brevet US5,193,809[1]. Son design fut aussi breveté le , sous le numéro de brevet D340,093.
Description
Le Square One est constitué de trois étages. Les étages du-dessus et du dessous sont tous deux faits de pièces triangulaires et trapézoïdales. Elles sont respectivement appelées arêtes et coins. Il y a en tout 8 pièces pour chaque type. Les coins font 60 degrés, tandis que les arêtes font 30 degrés. Chaque étage peut être tourné librement. Et si les pièces des trois étages sont alignées, il est possible de tourner la moitié du puzzle de 180 degrés, interchangeant les moitiés respectives des étages du haut et du bas. À partir de cela, il est très facile de mélanger le puzzle. Vu que les coins font précisément le double de l'angle d'une pièce triangulaire, on peut échanger librement les deux. Cependant, vu que l'étage du milieu ne peut prendre que deux formes, il y a une formule simple pour passer d'une forme à l'autre. Comme pour le Rubik's Cube et ses dérivés, les pièces sont colorées. Pour le résoudre, il faut qu'il soit en forme de cube, mais qu'il ait aussi une seule et unique couleur par face. Dans son état original (Résolu), si l'on se met devant la face avec le mot "Square-1" imprimé dessus, les couleurs sont : Blanc au-dessus, vert en bas, jaune devant, rouge à gauche, orange à droite, et bleu derrière. Les versions alternatives peuvent avoir un schéma de couleur différent.
Solution du Square-1
Méthode les sommets d'abord
La résolution se fait en deux phases bien distingues.
1- Notation:
La face Avant c'est la face avec l'équateur comportant le petit rectangle à gauche.
La couleur Haut, c'est la couleur-haut du sommet "correspondant" à l'équateur , càd dont les faces latérales ont les mêmes couleurs avec l'équateur voir fig1.
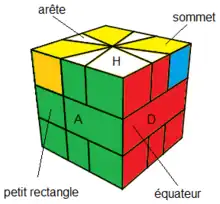
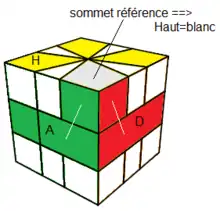
Pour nous les couleurs sont donc:
(H)aut=(b)lanc, (B)as=(j)aune, (A)vant=(v)ert, (P)ostérieur=(k)lein, (G)auche=(o)range, (D)roite=(r)ouge
Les rotations
1 sommet=2 arêtes
exemple: 3 - 2B /
3 = tourner 3 arêtes de la face Haut dans le sens horaire.
-2B = tourner 2 arêtes de la face Bas dans le sens contraire.
/ = tourner la moitié Droite 180° (/=lire slash)
Les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!
Phase I: Retrouver la forme cubique
Lorsqu'on mélange le Square-1, il donne des formes très bizarre... il faut d'abord le remettre sous la forme d'un cube. Pour cela on met le Bas sous la forme d'une "étoile" . On pousse donc tous ces 8 arêtes vers le Haut. Une fois le Bas a une étoile le Haut ne peut prendre que 5 formes distingues.
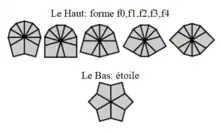
En poussant les arêtes vers le Haut on essaie de les regrouper ensemble pour avoir la forme f0 comme indique fig2
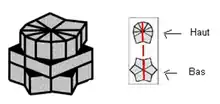
à partir de cette forme (f0) on reconstitue le Cube, la restauration se fait suivant le cas comme indique la fig3
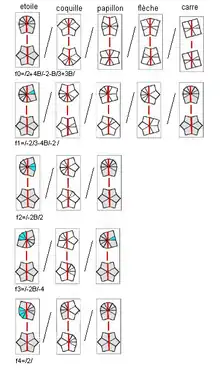
Parfois on a besoin de corriger l'équateur f=/6/6/
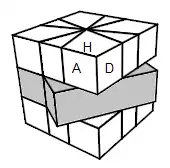
Phase II: Restituer les faces
Il faut d'abord chercher la couleur Haut. En tournant le Haut, cherchez un sommet "référence". La couleur Haut c'est la couleur-haut de ce sommet. S' il n'y a aucun sommet référence, c'est que la face Haut est en Bas, il faut donc la remonter avec: /6+6B/
1) Ranger les sommets Bas
Si un sommet Bas est dans une mauvaise position, on descend un autre à sa place ça lui force à remonter !!!
(HDA)->(BAD) = -B/ 3/ 3/ 6/ B
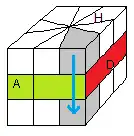
2) Permuter deux sommets Haut-Gauche
Echanger 2 sommets Haut-Gauche:
(HGP)<->(HAG) = 3/ -3+3B/ 3/ -3B/ 3B/ -3B/
On tourne H pour avoir un maximum de sommets bien placés !
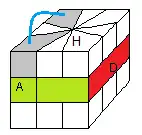
3) Ranger les arêtes Bas
On range les arêtes Bas par la formule:
(HD)->(BD) = 1/ -3B/ -1-4B/ 1+B/ 3B/ 3B/ -1
Si une arête Bas n'est pas à sa place, on descend n'importe quoi ça l'oblige à remonter !!!
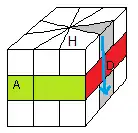
4) Ranger les arêtes Haut
On range les arêtes Haut par la formule
(HG)->(HD)->(HP) = 1/ -3B/ -1/ 3/ 1/ 3B/ -1 / -3/
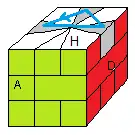
III Problème de parité
On a un problème de parité c'est quand on a 2 arêtes ou 2 sommets à échanger, voir la fig.
faites:
(HA)<->(HD) = /-3/ 3B/ -3B/ 3B/ 2/ 2B/ -2/ 4/ -2B/ 2B/ -1+4B/ 6-3B/ 6/
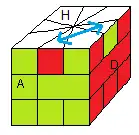
Remarque : On a 50% d'avoir la parité !
Commentaire
Un bon nombre de solutions pour ce puzzle existent sur Internet. Certaines emploient la méthode classique "étage par étage", tandis que d'autres procèdent d'une manière différente, en mettant d'abord les coins en place, puis les arêtes, ou vice versa. D'autres solutions encore, sont la combinaison de ces deux méthodes. Bien que toutes les solutions aient des approches différentes, la plupart essaient d'abord de rétablir le puzzle en forme de cube, sans tenir compte du deuxième étage, et de résoudre le puzzle en gardant sa forme de cube tout au long de la résolution. La plupart des solutions contiennent énormément d'algorithmes. Les algorithmes sont des séquences qui modifieront la position de certaines pièces du puzzle sans toucher au reste. Par exemple, interchanger deux pièces, échanger les deux étages, trianguler trois pièces, etc. Comme pour les solutions du Rubik's Cube, les solutions du Square-1 dépendent de l'utilisation des algorithmes. Les algorithmes ne peuvent être trouvés que par trois méthodes : Chercher, faire une erreur ou utiliser un ordinateur. Bien que les algorithmes d'un Rubik's Cube ne soient utiles qu'à la dernière étape, les algorithmes sont utiles pendant toute la résolution du Square-1. Dans ce dernier, l'échange libre de coins et arêtes peut poser problème, à cause de certains axes de rotation pouvant être physiquement bloqués.
Nombre de positions
Si toutes les rotations d'une permutation sont comptées une seule fois tandis que les réflexions sont comptées individuellement, il y a 170 × 2 × 8! × 8! = 552 738 816 000 positions. Si les réflexions et rotations sont comptées une seule fois seulement, le nombre de positions est réduit à 15! ÷ 3 = 435 891 456 000 positions.
Records récents
| Temps | Compétiteur | Nationalité | Lieu | Date |
|---|---|---|---|---|
| 3 s 87 | Michał Krasowski | Olsztyn Squared 2023 | 11 février 2023 | |
| 4 s 28 | Max Siauw | Big Cubes in Bothell 2022 | 10 décembre 2022 | |
| 4 s 33 | Elijah Rain Phelps | Naticube 2022 | 29 octobre 2022 | |
| Voir la suite ou | ||||
| Temps | Compétiteur | Nationalité | Lieu | Date |
|---|---|---|---|---|
| 5 s 02 | Max Siauw | CubingUSA Northeast Championship 2022 | 29 mai 2022 | |
| 6 s 06 | Sameer Aggarwal | Richmond Open B 2021 | 12 décembre 2021 | |
| 6 s 34 | David Epstein | Solving in Sale 2021 | 10 avril 2021 | |
| Voir la suite ou | ||||
La moyenne (ou average, terme anglais) est calculée sur cinq tentatives en enlevant à la fois le meilleur et le moins bon temps de la série, se basant ainsi sur trois temps.
Super Square One
Description
Le Super Square-1 est une version à quatre étages du Square-1. Tout comme le Square One, il peut prendre des formes non cubiques. Dès 2009, il est mis en vente par Uwe Mèffert dans son magasin en ligne de puzzles, Meffert's. Il est constitué de 8 pièces par étage, chacun entourant la même colonne, qui elle-même peut être tournée selon un axe perpendiculaire. Cela permet aux pièces des deux étages intérieurs et celles des deux étages extérieurs d'être échangées. Chaque étage est constitué de 4 coins et 4 arêtes. On peut dire que les coins et arêtes du Super Square-1 sont les mêmes que celles du Square-1 classique. On notera que le Super Square-1 a un centre sur les deux étages externes, ce qui peut démontrer l'existence de problèmes de parité sur le Square-1 classique.
Solution
Malgré son apparence, le Super Square-1 n'est pas plus difficile que le Square-1 classique. Les étages externes et internes sont en fait deux Square-1 indépendants. On peut ainsi utiliser la même méthode que le Square-1. Cependant, le centre des faces externes peut poser un défi supplémentaire.
 Super Square One résolu.
Super Square One résolu. Super Square One mélangé.
Super Square One mélangé. Super Square One mélangé.
Super Square One mélangé.
Nombre de positions
Sachant que le Super Square-1 est un groupement de deux Square-1 indépendants avec un centre sur les faces externes, on obtient un calcul assez simple : 4(170 × 2 × 8! × 8!)2 = 51 222 080 794 852 330 000 000 000 positions, soit plus de 50 quadrillons de positions.
Notes et références
- http://patft.uspto.gov/netacgi/nph-Parser?Sect1=PTO1&Sect2=HITOFF&d=PALL&p=1&u=/netahtml/PTO/srchnum.htm&r=1&f=G&l=50&s1=5,193,809.PN.&OS=PN/5,193,809&RS=PN/5,193,809
- La moyenne est calculée sur cinq tentatives en enlevant le meilleur et le moins bon temps.