Snark de Descartes
Dans la branche mathĂ©matique de la thĂ©orie des graphes, les snarks de Descartes sont une famille de graphes non orientĂ©s qui possĂšdent 210 sommets et 315 arĂȘtes. Ce sont des snarks.
| Snark de Descartes | |
| |
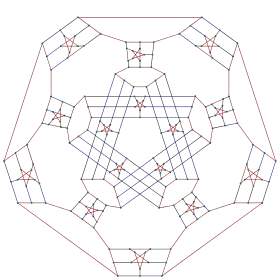
| Nombre de sommets | 210 |
|---|---|
| Nombre d'arĂȘtes | 315 |
| Maille | 5 |
| Indice chromatique | 4 |
| Propriétés | Cubique Snark |
Historique
Les snarks de Descartes ont été découverts en 1948 par William Tutte sous le pseudonyme Blanche Descartes[1].
Construction
On peut obtenir un snark de Descartes en partant du graphe de Petersen en remplaçant chaque sommet par un ennĂ©agone (polygone Ă neuf cĂŽtĂ©s) et chaque arĂȘte par le graphe ci-dessous. Le sous-graphe est lui aussi Ă©troitement liĂ© au graphe de Petersen. Comme il y a plusieurs façons de suivre cette procĂ©dure, il y a plusieurs snarks de Descartes.
Le point de départ, le graphe de Petersen
Les sommets en sont remplacĂ©s par des ennĂ©agones
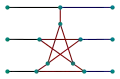Les arĂȘtes en sont remplacĂ©es par ce sous-graphe
Notes et références
(en) Cet article est partiellement ou en totalitĂ© issu de lâarticle de WikipĂ©dia en anglais intitulĂ© « Descartes snark » (voir la liste des auteurs).
- (en) Blanche Descartes, « Network Colorings », The Mathematical Gazette, Londres, no 32:299,â , p. 67 Ă 69 (lire en ligne).
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplĂ©mentaires peuvent sâappliquer aux fichiers multimĂ©dias.