Relation d'Euler dans le quadrilatère
La relation d'Euler dans le quadrilatère, découverte par Leonhard Euler en 1748[1], est une relation entre les longueurs des côtés d'un quadrilatère et celles de ses diagonales. C'est une généralisation de l'égalité du parallélogramme.
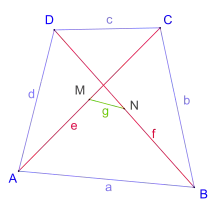
Énoncé et application
Dans un quadrilatère plan de côtés de longueurs , de diagonales de longueurs et , étant la distance entre les milieux des deux diagonales, la relation d'Euler s'écrit :
On trouvera une démonstration, utilisant la relation d'Al Kashi dans les quatre triangles formés par les côtés et les diagonales, dans [2].
Le quadrilatère étant un parallélogramme si et seulement si ses diagonales se coupent en leur milieu, autrement dit si et seulement si , on obtient le fait qu'un quadrilatère convexe est un parallélogramme si et seulement si la somme des carrés des longueurs de ses côtés est égale à la somme des carrés des longueurs de ses diagonales, ce qui généralise la règle du parallélogramme.
Généralisation et démonstration vectorielle
La relation ci-dessus est en fait valable pour tout quadruplet de points d'un espace affine euclidien, donc éventuellement non coplanaires, en l'écrivant sous la forme :
où sont les milieux de et .
Si l'on pose , alors et ; la relation d'Euler s'écrit donc :
ce qui se montre facilement en développant.
Notes et références
- (la) Leonhard Euler, Opera omnia, série 1, 26, p. 29-32
- (en) Deanna Haunsperger, Stephen Kennedy, The Edge of the Universe: Celebrating Ten Years of Math Horizons, MAA, (lire en ligne), p. 139
Voir aussi
Lien externe
- Eric W. Weisstein, "Quadrilateral" ; MathWorld.










![[AC]](https://img.franco.wiki/i/49b377aec839d74e0b48a42d2ba192d3efefc575.svg)
![{\displaystyle [BD]}](https://img.franco.wiki/i/746cf7b8dc56134be2fdb2b3819031eadc91eacd.svg)



