Rampe (fonction)
La fonction rampe (ou rampe) est la fonction réelle élémentaire définie par :
Cette fonction trouve son application en ingénierie, par exemple dans la théorie du traitement du signal.
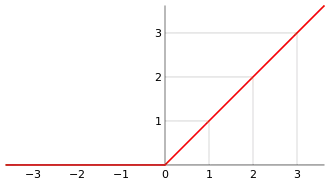
Graphe de la fonction rampe.
Définitions
La fonction rampe () peut être définie de différentes autres façons :
- la moyenne arithmétique de la variable et de la valeur absolue de celle-ci.
- Ceci peut se déduire de la définition de la fonction , avec et ;
- la fonction de Heaviside multipliée par l'application identité :
- la convolution de la fonction de Heaviside avec elle-même :
- l'intégrale de la fonction de Heaviside :
Propriétés analytiques
- La fonction rampe est positive sur la droite réelle, et même nulle pour tout réel négatif.
- Sa dérivée est la fonction de Heaviside :
- .
- Sa transformée de Fourier vaut
- ,
- où δ' désigne la dérivée de la distribution de Dirac.
- Sa transformée de Laplace vaut
- .
Lien externe
(en) Eric W. Weisstein, « Ramp function », sur MathWorld
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.











