Réseau complexe

Un graphe de réseau social est un graphe permettant de représenter les interactions spécifiques entre différents groupes de personnes, représenté respectivement par les liens et les nœuds du graphe. Ces interactions peuvent être très variées, comme des liens d'amitié ou de parenté, des activités professionnelles ou personnelles communes, ou encore partager les mêmes opinions[3]. Les réseaux sociaux en ligne en sont un bon exemple, où Facebook peut être vu comme un graphe non orienté, puisque les “amitiés” sont bidirectionnelles, et Twitter quant à lui est un graphe orienté, puisque les "abonnements" sont à sens unique[4].

Les réseaux d’information sont une autre catégorie de réseaux. Un exemple typique de ce type de réseau est le World Wide Web[5], où les nœuds correspondent aux pages web contenant de l’information, et les liens sont les hyperliens permettant de naviguer d’une page à l'autre. Ce réseau de plusieurs milliards de nœuds est un graphe dirigé, mais qui ne contient malgré tout pas de boucles fermées, puisqu’il n’y a pas de contraintes dans le classement des sites internet.

Les réseaux de citations des articles académiques sont également un bon exemple de réseau d’information[6]. Ces réseaux sont acycliques, puisque des articles ne peuvent citer que des travaux déjà publiés.

Nous pouvons également identifier les réseaux technologiques. Ce sont généralement des réseaux créés par l’Homme, comme les réseaux électriques[7], les réseaux de télécommunications, les réseaux aériens[7], les réseaux routiers[8] ou ferrés[9]. Mais, le réseau technologique le plus étudié est actuellement Internet[10], le réseau informatique mondial. Dans ce réseau, les ordinateurs et les routeurs sont les nœuds du réseau, et ces derniers sont connectés par des liens physiques comme la fibre optique modélisant les liens de ce réseau complexe.

Les réseaux complexes permettent également de représenter la majorité des systèmes biologiques. Ils sont de ce fait très étudiés en biologie des réseaux et en bio-informatique.

Les organismes vivants étant très complexes, le nombre de réseaux biologiques présents dans une cellule vivante est énorme. Ces réseaux complexes possèdent des fonctions spécifiques souvent indispensables au bon fonctionnement cellulaire. De plus, ces réseaux sont fortement interconnectés et fonctionnent de façon coordonnée et synchronisée avec une grande précision, puisque le moindre dysfonctionnement peut entraîner une maladie.

Parmi ces nombreux réseaux, nous pouvons citer les réseaux d’interaction protéine-protéine[11], les réseaux de régulation des gènes[12], les réseaux de signalisation ou encore les réseaux métaboliques[13]. Les réseaux métaboliques (ou voies métaboliques) sont un exemple typique de réseau biologique. Ils représentent l’ensemble des réactions biochimiques permettant de convertir un composé en un autre dans les cellules. Dans un tel réseau, les nœuds seront les molécules biochimiques et les liens les réactions ayant permis de les obtenir.

En plus de permettre de mieux comprendre le fonctionnement cellulaire complexe, l'analyse de ces réseaux permet d’identifier plus précisément les causes de différentes maladies, et ainsi de développer de nouveaux traitements, ce qui a même mené à la création d’une nouvelle discipline : la médecine des réseaux[14].

Figure 1 : Graphiques de la distribution des degrés selon le type de réseau[15]. A gauche, distribution des degrés pour un réseau aléatoire. A droite, distribution des degrés des nœuds pour un réseau réel.

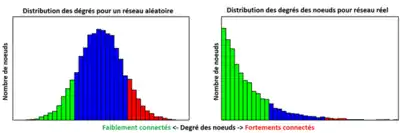
Le degré des nœuds d’un réseau est une des caractéristiques les plus importantes pour définir les réseaux complexes[16]. Le degré d'un nœud correspond au nombre de connexions qu’il possède avec les autres nœuds du réseau. Ainsi, plus le degré d'un nœud est élevé, plus le nœud d'un réseau est connecté et est important. Pour reprendre un exemple précédent, dans un réseau social, le nœud d'une personne avec 100 amitiés possède un degré de 100.

Nous pouvons ensuite étudier la distribution de ces degrés pour caractériser la structure d’un réseau. Cette fonction de distribution est définie comme la probabilité qu'un nœud sélectionné aléatoirement ait exactement k arêtes. Un réseau régulier à un degré simple, car chaque nœud est connecté à un nombre égal d'autres nœuds. On n'observe donc qu'un seul pic dans un graphique représentant la distribution des degrés. Pour un graphe aléatoire, les degré de distribution obéissent à un distribution de Poisson (Fig. 1, à gauche). Et, pour un réseau complexe, la distribution des degrés suit généralement une loi exponentielle et permet de caractériser de façon précise le type de réseau complexe d’un système (Fig. 1, à droite).

La longueur moyenne des (plus courts) chemins est une autre mesure robuste de la topologie d’un réseau. En choisissant deux nœuds quelconques dans un graphe, la distance entre ces nœuds correspond au nombre d'arêtes du plus petit chemin reliant ces deux nœuds. La longueur moyenne des chemins d'un réseau est donc définie comme la distance moyenne entre deux nœuds, moyennée sur tous les chemins disponibles entre ces nœuds[16].

L’analyse de cette propriété est très utile. Dans un réseau comme Internet, avoir une courte longueur moyenne des chemins permettra un transfert rapide des informations et de ce fait réduire les coûts de calculs. Et, dans un réseau électrique, minimiser cette longueur moyenne des plus courts chemins permet de réduire les déperditions d’énergie.

La plupart des réseaux réels ont une longueur de chemin moyenne très courte conduisant au concept d'un réseau « petit monde » où beaucoup des nœuds sont interconnectés par des chemins très courts.

Le coefficient de clustering, (aussi appelé coefficient d'agglomération, de connexion, de regroupement, d'agrégation ou de transitivité) est la probabilité que deux nœuds soient connectés sachant qu'ils ont un voisin commun[16].

Dans un réseau complexe, ce coefficient sera généralement élevé, puisqu’il est probable que des voisins d’un nœud soient également liés l’un de l’autre.

Figure 2 : Exemple de réseaux avec différents coefficient de clustering[17].

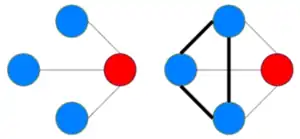
Dans l’image ci-contre (Fig. 2), nous pouvons voir sur le réseau de gauche que les 3 nœuds bleu sont reliés au nœud rouge, mais qu’ils ne forment pas de liaison entre eux. Dans le réseau à droite, tous les nœuds voisins du nœud rouge sont reliés entre eux. Ce dernier réseau à donc un coefficient de regroupement plus important.

Comme observé sur le graphique précédent, chaque voisin du nœud rouge (${\textstyle {i}}$) est connecté à chaque autre voisin du nœud rouge (${\textstyle {i}}$), alors au maximum il peut exister ${\textstyle {qi(qi-1)/2}}$ arêtes.

Ainsi, le coefficient de clustering ${\textstyle {Ci}}$ du nœud ${\textstyle {i}}$ (rouge) est défini comme :${\displaystyle Ci={\frac {2Ei}{qi(qi-1)}}}$

où ${\textstyle {Ci}}$est le rapport entre le nombre ${\textstyle {Ei}}$ de ponts qui existent parmi ces nœuds ${\textstyle {qi}}$ et le nombre total de ponts ${\textstyle {qi(qi-1)/2}}$. Pour le réseau le plus connecté à droite on obtient donc le calcul :

${\displaystyle Ci={\frac {2*3}{6(6-1)}}=0,20}$

Il existe différentes méthodes pour décomposer un réseau en sous-graphes de sommets.

Il est dans un premier temps possible de réaliser une décomposition basée sur les k-cores. Les k-cores sont des sous-graphes où chaque sommet possède au moins k voisins, avec k une valeur limite choisie par l’analyste et dépendante du graphe étudié. Cela a notamment permis d’étudier les clusters des réseaux sociaux ou décrire l'évolution des réseaux aléatoires et est fréquemment utilisé en bio-informatique pour visualiser les réseaux complexes[16] - [18].

Une autre méthode est la décomposition par k-truss. Les k-truss sont des sous graphes où chaque sommet est relié à au moins k-2 autres sommets. En d’autre termes, chaque sommet du k-truss fait partie de k-2 triangles formés à partir de nœuds de ce k-truss[19].

Il existe également des méthodes hybrides combinant la décomposition par k-core et la décomposition par k-truss comme la décomposition par noyaux. Technique qui emploie un ordre hiérarchique plus important que les deux méthodes séparées et pouvant révéler des groupes non détectés avec les méthodes précédentes[20].

Enfin, la décomposition topologique, dans laquelle le réseau est décomposé selon la distribution des degrés et la densité des noyaux. Cette approche permet de révéler la présence de groupes de nœuds partageant des densités similaires.

Ces groupes de fortes connectivité permettent d’identifier les nœuds centraux du réseau, qui possèdent potentiellement une fonction commune. Un bon exemple de ce procédé est l’étude des réseaux biologiques, en identifiant par exemple un groupe de protéines impliquées dans un symptôme important d’une maladie[21].

Une fois que le nombre de nœud du réseau à diminué, il est tout à fait possible d’appliquer les différentes métriques classique d’analyse de réseau, comme la connectivité du réseau (distribution des degrés), la distance du réseau et de ses composants (Exemple : Réseau « petit monde »), la centralité intermédiaire des nœuds, ou encore des métriques de similarité des nœuds. Il sera également possible d’utiliser des algorithmes de partitionnement des données, comme les méthodes de K-means ou de clustering hiérarchique[22].

La classification d’un graphe repose généralement sur plusieurs paramètres définit précisément, comme le coefficient de clustering ${\textstyle {C(p)}}$ et la longueur de chemin ${\textstyle {L(p)}}$. Classiquement, un réseau est considéré comme étant de type « petit monde » si le plus court chemin entre deux nœuds choisis aléatoirement croît de façon logarithmique en fonction du nombre de nœuds du réseau. Mais, il existe également plusieurs métriques spécifiques ayant pour but de déterminer si un réseau est un réseau « petit monde » ou non. L'une d'entre elles est le ratio entre le réseau supposé « petit monde » et un réseau aléatoire. Cette métrique (${\textstyle {\sigma }}$)[26] indiquera donc dans quelle mesure un réseau est de type « petit monde ». Si ${\textstyle {\sigma }}$ > 1 alors celui peut être considéré comme un réseau « petit monde ».

${\displaystyle \sigma ={\frac {\frac {C}{C_{r}}}{\frac {L}{L_{r}}}}}$

Ce ratio σ est grandement influencé par la taille du réseau, ce qui rend son appréciation difficile. Pour pouvoir mesurer la capacité d’un réseau à être de type « petit monde », il est également possible d’utiliser la différence du ratio entre un réseau aléatoire et un réseau voulu.

${\displaystyle \omega ={\frac {L_{rand}}{L}}-{\frac {C}{C_{latt}}}}$

${\textstyle {L_{rand}}}$ et ${\textstyle {C}}$ correspondent respectivement aux valeurs de longueur de chemin et du coefficient de clustering d’un réseau aléatoire, tandis que ${\textstyle {C_{latt}}}$ correspond à un réseau équivalent. ${\textstyle {\omega }}$[26] va varier entre -1 et 1 quelle que soit la taille du réseau. Plus la valeur de ω est proche de zéro plus le réseau est considéré comme « petit monde ». Des valeurs positives indiquent un caractère aléatoire dans le réseau. Des valeurs négatives indiquent un caractère plus régulier dans la composition du réseau. Le modèle de réseau « petit monde », Watts et Strogatz définissent les paramètres d’un réseau avec une petite valeur de ${\textstyle {L}}$ qui est représentatif des graphes dit "aléatoires" et une valeur de clustering ${\textstyle {C}}$ très élevé représentatif des graphes plus réguliers.

Les domaines d’application d’un réseau « petit monde » sont variés. On les retrouve en sociologie, avec les réseaux sociaux. Dans ces réseaux, il est question de la capacité d’une information à se transmettre à travers l’ensemble d’un réseau par les individus et comment l’affinité des membres peut influer sur cette même capacité de transmission.

Dans une application plus concrète comme la gestion des fermetures des aéroports. Grâce à l’application du réseau « petit monde », il est possible d’expliquer pourquoi la fermeture de certains aéroports ou lieux de transit obligerait les voyageurs à faire escale plus souvent que la normale.

On les retrouve également en informatique[27], ou l’étude des réseaux « petit monde », a permis de mieux comprendre comment stocker et gérer les informations dans un base de données pour rendre accessible le plus rapidement possible dans le futur une information pour l’utilisateur.

Enfin, ces réseaux sont présents en sciences biologiques et plus particulièrement dans les neurosciences[28]. Ici il est question de pouvoir adapter et comparer un réseau « petit monde » à un réseau cérébral. La plupart des études se sont intéressées à la comparaison sur l’anatomie et la structure des réseaux, l’aspect fonctionnel mais aussi les interactions entre nœuds et arêtes. Dans certains cas, il a été question d’utiliser ce genre de réseau pour mimer les AVC et les crises d'épilepsie[29]. Dans le cadre de la microbiologie par exemple, on étudiera la capacité de transmission des plasmides ou de l’information génétique liés à la résistance bactérienne ou virale.

Pour la plupart des applications pratiques, l'espace de ces réseaux est un espace bidimensionnel, et la valeur associée aux nœuds est la distance euclidienne classique[30]. Cela implique en général que la probabilité de trouver un lien entre deux nœuds diminue avec la distance. Cependant, cela n'implique pas forcément qu'un réseau spatial soit planaire. Par exemple, le réseau aérien reliant les aéroports du monde entier n'est pas un réseau planaire, soit un réseau qui peut être représenté dans un plan de façon ou ses liens ne se croisent pas. Avec cette définition d'un réseau spatial, les liens ne sont pas nécessairement dans l'espace : les réseaux sociaux par exemple relient les individus à travers des relations d'amitié. Dans ce cas, l'espace intervient dans le fait que la probabilité de connexion entre deux individus diminue généralement avec la distance qui les sépare. Cependant, de nombreux réseaux d'infrastructure seront inévitablement planaires. En plus d’être des réseaux spatiaux, les routes, le rail et les autres réseaux de transport sont principalement des réseaux planaires.