Problème de couverture par sommets

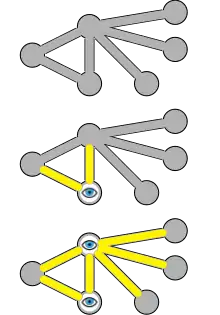
Une couverture par sommets ou transversal d'un graphe G est un ensemble C de sommets tel que chaque arête de G = (V, E) est incidente à au moins un sommet de C, ie un sous-ensemble de sommets ${\displaystyle S\subseteq V}$ tel que pour chaque arête ${\displaystyle (u,v)}$ de ${\displaystyle G}$ on a ${\displaystyle u\in S}$ ou ${\displaystyle v\in S}$. On dit que l'ensemble C couvre les arêtes de G. La figure suivante montre des exemples de couvertures des sommets de deux graphes (l'ensemble C est formé des sommets rouges).

Une couverture minimale par sommets est une couverture des sommets de taille minimale. La figure suivante montre des exemples de couvertures minimales des sommets dans les mêmes graphes que ci-dessus.

Si un ensemble de sommets ${\displaystyle S}$ est un transversal, son complément ${\displaystyle {\bar {S}}=V\setminus S}$ est un stable (ou ensemble indépendant). Donc un graphe à n sommets a un transversal de taille k si et seulement s'il a un stable de taille n - k. On en déduit immédiatement le résultat suivant[2] :

où α(G) désigne la taille d'un stable maximum, τ(G) désigne la taille d'un transversal minimum et ${\displaystyle n=|V|}$.

Le problème d'optimisation, appelé problème de la couverture minimum par sommets, est le suivant :

Entrée : un graphe G

Question : quel est le plus petit entier k, tel qu'il existe une couverture par sommets de G de taille k ?

et le problème de décision :

Entrée : un graphe G et un entier k

Question : existe-t-il une couverture par sommet de G de taille k ?

Le programme d'optimisation linéaire en nombres entiers associé est :

minimiser	${\displaystyle \sum _{v\in V}x_{v}}$			(minimiser le coût total)
tel que	${\displaystyle x_{u}+x_{v}\geq 1}$	pour tout ${\displaystyle \{u,v\}\in E}$		(toutes les arêtes sont couvertes)
	${\displaystyle x_{v}\in \{0,1\}}$	pour tout ${\displaystyle v\in V}$.		(chaque sommet est dans la couverture ou non)

La relaxation linéaire de ce système est le dual de la relaxation du programme d'optimisation pour le problème du couplage maximum[3].