Probabilités des dés
Les probabilités des résultats obtenus par lancer de dés ont fait l'objet de nombreuses études mathématiques. En effet, ce type de générateur de nombres aléatoires est à la base de nombreux jeux de société.
Application des lois de probabilité
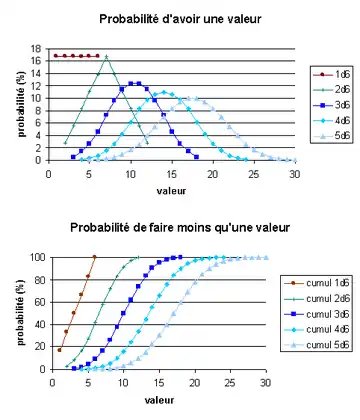
Pour un simple lancer d'un seul dé à 6 faces, qu'on considère équilibré, la probabilité d'obtenir n'importe quelle valeur 1 à 6 est exactement de 1/6. Le tirage suit donc une loi uniforme discrète. Le tirage de n dés suit une loi multinomiale dont les probabilités p1, p2, …, p6 sont toutes égales à 1/6, si le dé n'est pas pipé.
Si on jette deux dés et qu'on additionne les nombres obtenus sur les deux faces supérieures, les tirages ne sont plus distribués de façon uniforme mais suivent une distribution triangulaire :
| Somme des dés | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Probabilité | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
Le tirage le plus probable est alors 7.
Il y a un certain nombre de combinaisons possibles avec deux dés à 6 faces pour obtenir un certain nombre : (Rappel : le chiffre 6 est le chiffre maximum, car c'est le nombre de faces)
- 1+1 =2
- 1+2 et 2+1 =3
- 1+3; 2+2 et 3+1 =4
- 1+4; 2+3; 3+2 et 4+1 =5
- 1+5; 2+4; 3+3; 4+2 et 5+1 =6
- 1+6; 2+5; 3+4; 4+3; 5+2 et 6+1 =7
- 2+6; 3+5; 4+4; 5+3 et 6+2 =8
- 3+6; 4+5; 5+4 et 6+3 =9
- 4+6; 5+5 et 6+4 =10
- 5+6 et 6+5 =11
- 6+6=12
On peut aussi appliquer ceci sous forme de tableau:
| N° | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Avec trois dés ou plus, la distribution se rapproche d'une distribution normale avec l'ajout de chaque dé (conséquence du théorème central limite). La distribution de probabilité exacte pour un nombre de dés peut être calculée par convolution répétée de la distribution de probabilité d'un dé simple avec elle-même :
- Fi(m ) = ∑n F1(n ) Fi-1(m - n ).
La somme variant de 1 à d lorsque les dés ont d faces et que les faces sont numérotées de 1 à d.
Voir aussi
- Loi triangulaire
- Calculs des probabilités pour le jeu du Martinetti
Bibliographie
- (en) Catalin Barboianu, Probability Guide to Gambling. The Mathematics of Dice, Slots, Roulette, Baccarat, Blackjack, Poker, Lottery and Sport Bets, INFAROM Publishing, , 316 p. (ISBN 973-87520-3-5, présentation en ligne, lire en ligne).
- (en) Paul J. Nahin, Digital Dice. Computational Solutions to Practical Probability Problems, Princeton University Press, , 263 p. (ISBN 978-0-691-12698-2 et 0-691-12698-4, présentation en ligne, lire en ligne).
- Martine Quinio Benamo, Probabilités et statistique aujourd'hui. Pourquoi faire? Comment faire?, Paris/Budapest/Kinshasa etc., L'Harmattan, , 273 p. (ISBN 2-7475-9799-7, lire en ligne)
- Bernard Ycart, Modèles et Algorithmes Markoviens, Berlin/Heidelberg/New York etc., Springer, , 272 p. (ISBN 3-540-43696-0, lire en ligne)
- Maurice Fréchet et Maurice Halbwachs, Le calcul des probabilités à la portée de tous, Dunod, , 297 p.

