Polynôme de Laguerre

En mathématiques, les polynômes de Laguerre, nommés d'après Edmond Laguerre, sont les solutions normalisées de l'équation de Laguerre :

x\,y''+(1-x)\,y'+n\,y=0\,

qui est une équation différentielle linéaire homogène d'ordre 2 et se réécrit sous la forme de Sturm-Liouville :

$-{{\rm {d}} \over {\rm {d}}x}\left(x{\rm {e}}^{-x}{{\rm {d}}y \over {\rm {d}}x}\right)=n{\rm {e}}^{-x}y.$

Cette équation a des solutions non singulières seulement si $n$ est un entier positif. Les solutions $L n$ forment une suite de polynômes orthogonaux dans $L 2$ (ℝ⁺, $e - x d x$ ), et la normalisation se fait en leur imposant d'être de norme 1, donc de former une famille orthonormale. Ils forment même une base hilbertienne de $L 2$ (ℝ⁺, $e - x d x$ ).

Cette suite de polynômes peut être définie par la formule de Rodrigues

L_{n}(x)={\frac {\mathrm {e} ^{x}}{n!}}{\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\left(\mathrm {e} ^{-x}x^{n}\right).

La suite des polynômes de Laguerre est une suite de Sheffer.

Les polynômes de Laguerre apparaissent en mécanique quantique dans la partie radiale de la solution de l'équation de Schrödinger pour un atome à un électron[1].

Le coefficient dominant de $L n$ est $(-1) n / n!$ . Les physiciens utilisent souvent une définition des polynômes de Laguerre où ceux-ci sont multipliés par $(-1) n n!$ , obtenant ainsi des polynômes unitaires.

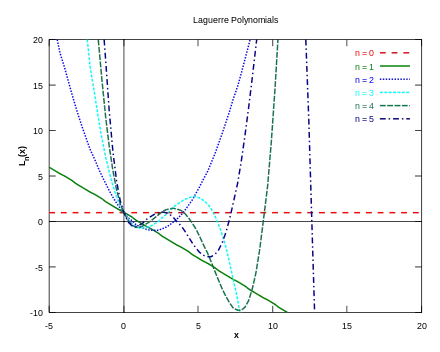
Les premiers polynômes

Voici les premiers polynômes de Laguerre :

n	$L_{n}(x)\,$
0	$1\,$
1	$-x+1\,$
2	${\begin{matrix}{\frac {1}{2}}\end{matrix}}(x^{2}-4x+2)\,$
3	${\begin{matrix}{\frac {1}{6}}\end{matrix}}(-x^{3}+9x^{2}-18x+6)\,$
4	${\begin{matrix}{\frac {1}{24}}\end{matrix}}(x^{4}-16x^{3}+72x^{2}-96x+24)\,$
5	${\begin{matrix}{\frac {1}{120}}\end{matrix}}(-x^{5}+25x^{4}-200x^{3}+600x^{2}-600x+120)\,$
6	${\begin{matrix}{\frac {1}{720}}\end{matrix}}(x^{6}-36x^{5}+450x^{4}-2400x^{3}+5400x^{2}-4320x+720)\,$

Les six premiers polynômes de Laguerre

Propriétés

Transformée de Laplace des polynômes de Laguerre dans ℝ⁺

En désignant $H (x)$ comme étant la fonction de Heaviside, on a l'égalité :

{\mathcal {L}}\left\{H(x)L_{n}(x)\right\}={\mathcal {L}}\left\{H(x){\frac {\mathrm {e} ^{x}}{n!}}{\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\left(\mathrm {e} ^{-x}x^{n}\right)\right\}={\frac {n!}{z}}\left({\frac {z-1}{z}}\right)^{n}

Démonstration

Calcul de ${\mathcal {L}}\{H(x)x^{n}\}$

{\mathcal {L}}\{H(x)x^{n}\}=A_{n}(z)=\int _{0}^{+\infty }x^{n}{\rm {e}}^{-zx}{\rm {d}}x

Après intégrations par parties successives, on trouve :

A_{n}(z)={\frac {n}{z}}A_{n-1}(z)=......={\frac {n!}{z^{n}}}A_{0}(z)={\frac {n!}{z^{n+1}}}

Calcul de ${\mathcal {L}}\{H(x)x^{n}{\rm {e}}^{-x}\}$

On rappelle que:

{\mathcal {L}}\{H(x)f(x){\rm {e}}^{-x}\}=F(z+1)

avec

F(z)={\mathcal {L}}\{H(x)f(x)\}

Alors :

{\mathcal {L}}\{H(x)x^{n}{\rm {e}}^{-x}\}=\int _{0}^{+\infty }x^{n}{\rm {e}}^{-x(1+z)}{\rm {d}}x=B_{n}(z)=A_{n}(z+1)={\frac {n!}{(z+1)^{n+1}}}={\mathcal {L}}\{H(x){\rm {e}}^{-x}x^{n}\}

Calculons maintenant la transformée de Laplace de $H(x){\rm {e}}^{x}{\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\{x^{n}{\rm {e}}^{-x}\}$

{\mathcal {L}}\left\{H(x){\rm {e}}^{x}{\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\{x^{n}{\rm {e}}^{-x}\}\right\}=\int _{0}^{+\infty }{\rm {e}}^{x}{\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\{x^{n}{\rm {e}}^{-x}\}{\rm {e}}^{-zx}{\rm {d}}x

En utilisant la formule de Leibniz :

(fg)^{(n)}=\sum _{p=0}^{n}{n \choose p}f^{(p)}g^{(n-p)}\Rightarrow (x^{n}{\rm {e}}^{-x})^{(n)}=\sum _{p=0}^{n}{n \choose p}(x^{n})^{(p)}({\rm {e}}^{-x})^{(n-p)}=\sum _{p=0}^{n}{n \choose p}{\frac {n!}{(n-p)!}}x^{n-p}(-1)^{n-p}{\rm {e}}^{-x}

Donc

{\mathcal {L}}\left\{H(x){\rm {e}}^{x}{\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\{x^{n}{\rm {e}}^{-x}\}\right\}=\sum _{p=0}^{n}{n \choose p}{\frac {n!(-1)^{n-p}}{(n-p)!}}\int _{0}^{+\infty }x^{n-p}{\rm {e}}^{-zx}{\rm {d}}x

Il en résulte

{\mathcal {L}}\left\{H(x){\frac {\mathrm {e} ^{x}}{n!}}{\frac {{\rm {d}}^{n}}{{\rm {d}}x^{n}}}\left(\mathrm {e} ^{-x}x^{n}\right)\right\}={\frac {n!}{z}}\left({\frac {z-1}{z}}\right)^{n}

Fonction génératrice

La fonction génératrice pour les polynômes de Laguerre est $\sum _{n=0}^{\infty }L_{n}(x){\frac {t^{n}}{n!}}\,={\frac {{\rm {e}}^{-xt/(1-t)}}{1-t}}$ .

Démonstration

Calculons tout d'abord la transformée de Laplace de la fonction génératrice des polynômes de Laguerre:

{\mathcal {L}}\left\{\sum _{n=0}^{\infty }L_{n}(x){\frac {t^{n}}{n!}}\right\}=\sum _{n=0}^{\infty }{\mathcal {L}}\{L_{n}(x)\}{\frac {t^{n}}{n!}}=\sum _{n=0}^{\infty }{\frac {n!}{z}}\left({\frac {z-1}{z}}\right)^{n}{\frac {t^{n}}{n!}}={\frac {1}{z}}\sum _{n=0}^{\infty }\left(t-{\frac {t}{z}}\right)^{n}

La convergence de cette série est assurée pour $\left|t-{\frac {t}{z}}\right|<1$ . Dans ces conditions on a

\sum _{n=0}^{\infty }\left(t-{\frac {t}{z}}\right)^{n}=\lim \limits _{n\to \infty }{\frac {1-(t-{\frac {t}{z}})^{n+1}}{1-(t-{\frac {t}{z}})}}={\frac {1}{1-t+{\frac {t}{z}}}}

Donc

{\mathcal {L}}\left\{\sum _{n=0}^{\infty }L_{n}(x){\frac {t^{n}}{n!}}\right\}={\frac {1}{z}}{\frac {1}{1-t+{\frac {t}{z}}}}={\frac {1}{1-t}}{\frac {1}{z+{\frac {t}{1-t}}}}={\frac {1}{1-t}}{\mathcal {L}}\left\{{\rm {e}}^{-x{\frac {t}{1-t}}}\right\}

car

{\mathcal {L}}\{{\rm {e}}^{-ax}\}={\frac {1}{z+a}}

On en déduit finalement

\sum _{n=0}^{\infty }L_{n}(x){\frac {t^{n}}{n!}}={\frac {1}{1-t}}{\rm {e}}^{-x{\frac {t}{1-t}}}

Équations diverses

Le n-ième polynôme de Laguerre satisfait l'équation différentielle suivante :

xL_{n}''(x)+(1-x)L_{n}'(x)+nL_{n}(x)=0.\,

On a aussi la suite récurrente suivante :

(n+1)L_{n+1}(x)+(x-2n-1)L_{n}(x)+nL_{n-1}(x)=0.\,

Les polynômes respectent la propriété

xL_{n}'(x)-nL_{n}(x)+nL_{n-1}(x)=0.\,

Expression par une intégrale de contour

Les polynômes peuvent être exprimés en termes d'une intégrale de contour

L_{n}(x)={\frac {1}{2\pi {\rm {i}}}}\oint {\frac {{\rm {e}}^{-xt/(1-t)}}{(1-t)\,t^{n+1}}}\,{\rm {d}}t

où le contour entoure l'origine une fois dans le sens trigonométrique.

Polynômes de Laguerre généralisés

La propriété d'orthogonalité évoquée plus haut revient à dire que si $X$ est une variable aléatoire distribuée exponentiellement avec la fonction densité de probabilité

f(x)=\left\{{\begin{matrix}{\rm {e}}^{-x}&{\mbox{si}}\ x>0,\\0&{\mbox{si}}\ x<0,\end{matrix}}\right.

alors

\mathbb {E} (L_{n}(X)L_{m}(X))=0\ {\mbox{si}}\ n\neq m.

La distribution exponentielle n'est pas la seule distribution Gamma. Une suite de polynômes orthogonaux par rapport à la distribution gamma dont la fonction densité de probabilité est, pour $α > -1$ ,

f(x)=\left\{{\begin{matrix}x^{\alpha }{\rm {e}}^{-x}/\Gamma (1+\alpha )&{\mbox{si}}\ x>0,\\0&{\mbox{si}}\ x<0,\end{matrix}}\right.

(cf.fonction gamma) est donnée par la formule de Rodrigues pour les polynômes de Laguerre généralisés:

L_{n}^{(\alpha )}(x)={x^{-\alpha }{\rm {e}}^{x} \over n!}{{\rm {d}}^{n} \over {\rm {d}}x^{n}}\left({\rm {e}}^{-x}x^{n+\alpha }\right).

Ils sont parfois appelés les polynômes de Laguerre associés. On retrouve les polynômes de Laguerre simples en prenant $α = 0$ :

L_{n}^{(0)}(x)=L_{n}(x).

Les polynômes de Laguerre généralisés sont orthogonaux sur $[0 , \infty[$ par rapport à la fonction de poids $x α e - x$ :

\int _{0}^{\infty }{\rm {e}}^{-x}x^{\alpha }L_{n}^{(\alpha )}(x)L_{m}^{(\alpha )}(x){\rm {d}}x={\frac {\Gamma (n+\alpha +1)}{n!}}\delta _{nm}.

Les polynômes de Laguerre généralisés obéissent à l'équation différentielle

xL_{n}^{(\alpha )\prime \prime }(x)+(\alpha +1-x)L_{n}^{(\alpha )\prime }(x)+nL_{n}^{(\alpha )}(x)=0.\,

Exemples de polynômes de Laguerre généralisés

Les premiers polynômes de Laguerre généralisés sont

L_{0}^{(\alpha )}(x)=1

L_{1}^{(\alpha )}(x)=-x+\alpha +1

L_{2}^{(\alpha )}(x)={\frac {x^{2}}{2}}-(\alpha +2)x+{\frac {(\alpha +2)(\alpha +1)}{2}}

L_{3}^{(\alpha )}(x)={\frac {-x^{3}}{6}}+{\frac {(\alpha +3)x^{2}}{2}}-{\frac {(\alpha +2)(\alpha +3)x}{2}}+{\frac {(\alpha +1)(\alpha +2)(\alpha +3)}{6}}

Dérivées des polynômes de Laguerre généralisés

Le calcul de la dérivée d'ordre $k$ de la représentation en série d'un polynôme de Laguerre généralisé fois conduit à

{\frac {\mathrm {d} ^{k}}{\mathrm {d} x^{k}}}L_{n}^{(\alpha )}(x)=(-1)^{k}L_{n-k}^{(\alpha +k)}(x).

Relation aux polynômes d'Hermite

Les polynômes de Laguerre généralisés apparaissent dans le traitement de l'oscillateur harmonique quantique, à cause de leur relation aux polynômes d'Hermite, qui peuvent être exprimés par

H_{2n}(x)=(-1)^{n}\,2^{2n}n!\,L_{n}^{(-1/2)}(x^{2})

H_{2n+1}(x)=(-1)^{n}\,2^{2n+1}n!\,xL_{n}^{(1/2)}(x^{2})

où les $H_{n}(x)$ sont les polynômes d'Hermite.

Relation aux fonctions hypergéométriques

Les polynômes de Laguerre peuvent être reliés aux fonctions hypergéométriques, plus précisément à la fonction hypergéométrique confluente, par

L_{n}^{(\alpha )}(x)={n+\alpha  \choose n}M(-n,\alpha +1,x)={\frac {(\alpha +1)_{n}}{n!}}\,_{1}F_{1}(-n,\alpha +1,x)

où $(a)_{n}$ est le symbole de Pochhammer (qui, dans ce cas particulier, est utilisé pour représenter la factorielle croissante $a(a+1)(a+2)...(a+n-1)$ ).

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Laguerre polynomials » (voir la liste des auteurs).

(en) The Legendre and Laguerre Polynomials & the Elementary Quantum Mechanical Model of the Hydrogen Atom, par Timothy Jones

Voir aussi

Liens externes

(en) Eric W. Weisstein, « Laguerre Polynomial », sur MathWorld
(en) Eric W. Weisstein, « Associated Laguerre Polynomial », sur MathWorld

Bibliographie

(en) George Arfken et Hans Weber, Mathematical Methods for Physicists, Academic Press, 2000 (ISBN 0-12-059825-6)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.