Planimètre
Le planimètre est un outil qui permet la mesure mécanique directe des surfaces sur les plans, cartes géographiques, etc., en suivant le contour par l'extrémité d'un bras articulé.

Le planimètre a inspiré l'invention de la souris (informatique) : Douglas Engelbart a construit le premier prototype de souris à partir de la technologie du planimètre[1].
Planimètre polaire d'Amsler
Inventé en 1854 par le Suisse Jakob Amsler-Laffon (1823-1912), il est simple, précis et bon marché (brevet français 24338 pour 15 ans du [2]).
Description et fonctionnement
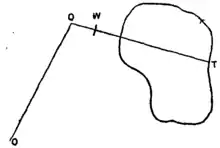
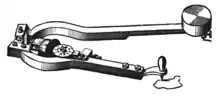
Le planimètre d'Amsler se compose de deux bras articulés, le bras polaire, et le bras extérieur. Une extrémité du bras polaire peut tourner autour d'un point fixe (généralement immobilisé par une masse). Le bras extérieur est fixé à l'autre extrémité du bras polaire, autour de laquelle elle est libre de tourner. À l'extrémité du bras extérieur se trouve le curseur avec lequel l'opérateur suit le périmètre de la figure dont il veut mesurer la surface. Le bras extérieur porte de plus une roue, qui permet de mesurer les déplacements perpendiculaires au bras.
Lorsque la roue glisse en se déplaçant, elle subit toujours une force de frottement dans la direction du glissement. Comme la roue peut tourner sur son axe, la seule force de frottement qu'elle peut transmettre au bras extérieur est parallèle à cet axe, puisqu'une force perpendiculaire la ferait immédiatement tourner: la roue tourne toujours de manière que la force de frottement transmise soit en permanence parallèle à son axe. La roue décompose donc en permanence les déplacements de son point de contact en un déplacement parallèle à l'axe (qui entraîne un frottement) et un déplacement perpendiculaire (qui la fait tourner).
Lorsque le curseur est déplacé dans une direction perpendiculaire au bras extérieur, la roue tourne, et sa rotation est proportionnelle au déplacement du curseur. Lorsqu'il est déplacé dans la direction du bras extérieur, en revanche, la roue glisse sans tourner, et n'enregistre pas de déplacement. Globalement, la rotation de la roue intègre la projection du déplacement du curseur sur la direction perpendiculaire au bras extérieur.
Or, lorsque le curseur décrit une courbe fermée, cette intégrale est proportionnelle à la surface délimitée par la courbe.
Démonstration
Le théorème de Green relie l'intégrale curviligne d'un champ le long d'une courbe fermée avec l'intégrale du rotationnel de ce champ sur la surface correspondante:
Ici, le dispositif intègre donc un champ de vecteurs F qui associe en chaque point M du plan atteint par le curseur un vecteur unitaire perpendiculaire au bras S, dans la position qu'il prend en ce point.
On démontre (tout calcul fait) que le rotationnel de ce champ est constant. L'intégrale sur la surface est donc simplement proportionnelle à cette surface.
Planimètre de Prytz
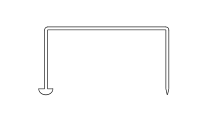
Ce planimètre, inventé à la fin du XIXe siècle par Holger Prytz[3], officier de cavalerie Danois et mathématicien, est remarquable par son côté extrêmement rudimentaire. Il consiste en une simple tige en forme de U, dont une extrémité, appelée le curseur, se termine en pointe, et dont l'autre extrémité est généralement taillée en une petite lame parallèle au plan de la tige pour éviter tout glissement perpendiculaire à ce plan (une roulette remplirait le même rôle). Le fil de la lame est généralement un peu courbe, ce qui donne à l'instrument l'allure générale d'une hachette, nom également attribué à ce planimètre.
On fait parcourir au curseur la frontière de la surface à mesurer. Ce faisant, la lame située à l'autre extrémité suit une courbe tractrice, telle que la tangente en tout point de la tractrice reste colinéaire au bras horizontal de la tige du planimètre. Lorsque le curseur a parcouru la courbe, la lame ne se retrouve pas à sa position initiale. Si la longueur de la tige est assez grande pour que le planimètre n'ait pas fait un tour complet sur lui-même, l'angle dont a varié la tige est à peu près proportionnel à la surface. La valeur mesurée de la surface est obtenue en multipliant la longueur L du bras par le déplacement de la lame entre sa position initiale et sa position finale, le long de l'arc de cercle dont le rayon est formé par le bras de la tige et dont le centre est la position initiale (ou finale) du curseur.
C'est un instrument bon marché mais peu précis du fait de l'existence d'une erreur systématique. Cette erreur est inversement proportionnelle à la longueur L du bras de sorte que sa précision augmente avec cette longueur. L'erreur provient du fait que la surface mesurée diffère de la surface réelle par une quantité égale à l'aire algébrique du domaine délimité par la trajectoire suivie par la lame (y compris l'arc de cercle final). Il n'est pas facile de compenser exactement cette erreur systématique. Tout au plus peut-on l'atténuer en s'arrangeant pour que les écarts de la trajectoire de la lame soient répartis de manière à peu près équilibrée de part et d'autre de l'arc de cercle.
Soit (X,Y) les coordonnées du curseur, et (x,y) celle de la lame. Soit l'angle que fait le bras du planimètre avec l'axe Ox. On a donc :
Soit . On vérifiera que :
- .
On intègre ces formes différentielles lors du parcours suivi par le planimètre (y compris la rotation finale pour le ramener à sa position initiale). D'après le théorème de Green, l'intégrale de est l'aire A cherchée. L'intégrale de est l'aire du domaine limité par la courbe parcourue par la lame. Elle va donner l'erreur systématique E. L'intégrale de est nulle car on intègre alors une différentielle exacte sur un parcours fermé. Il en est de même de l'intégrale de à condition que le planimètre n'ait pas fait de tour complet sur lui-même entre sa position initiale et finale. On obtient donc la relation :
Tant qu'on est dans la phase de parcours du curseur, est nul car la lame se déplace parallèlement à la tige. Seule la rotation finale apporte une contribution non nulle à cette intégrale, mais alors , de sorte qu'on obtient la relation annoncée :

Une autre source d'imprécision est que le déplacement du bras est souvent mesuré en distance rectiligne, alors que pour une meilleure précision il devrait l'être suivant sa trajectoire curviligne de retour. Pour compenser cette imprécision, le bras de certains planimètres est courbe, et porte une graduation le long de laquelle la mesure du déplacement peut être faite. Prytz ne manquait pas d'ironiser sur cette amélioration apportée à son planimètre, car elle ne pouvait supprimer l'erreur systématique et enlevait à son planimètre son intérêt rudimentaire[4].
Voir aussi
Articles connexes
Liens externes
- Marie-José Durand-Richard, Loïc Petitgirard, Les instruments du calcul savant : Planimètre polaire d'Amsler et intégraphe, CNRS
- (en) Paul Kunkel, The Planimeter But what about a polar planimeter?, , une jolie démonstration.
- (en) Un site sur les planimètres
- (en) fonctionnement d'un planimètre de Prytz
- Une vidéo montrant l'utilisation d'un planimètre.
Références
- « L’évolution de la souris d’ordinateur », sur www.journaldunet.com (consulté le )
- GoogleBooks : Catalogue des brevets d'invention (1855), Paris 1856, p. 273
- (da) H. Pritz, « Stangplanimetret », Den Tekniske Forenings Tidsskrift, no 10, , p. 23-28 (lire en ligne)
- (en) Robert Foote, Mark Levi et Serge Tabachnikov, « Tractrices, bicycle tire tracks, hatchet planimeters, and a 100-year-old conjecture », Amer. Math Monthly, vol. 120, no 3, , p. 199-216 (DOI 10.4169/amer.math.monthly.120.03.199)
















