Plan de Sorgenfrey

En mathématiques, le plan de Sorgenfrey est un espace topologique souvent utilisé, à plusieurs titres, comme contre-exemple[1]. C'est le produit S×S de la droite de Sorgenfrey S par elle-même. Robert Sorgenfrey a démontré que le plan S×S est non normal (donc non paracompact), tandis que la droite S est paracompacte (donc normale)[2].

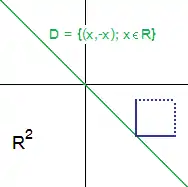
Plan de Sorgenfrey avec l’antidiagonale comme sous-espace.

Définition

Le plan de Sorgenfrey S×S est l'ensemble produit ℝ×ℝ, muni de la topologie dont une base d'ouverts est constituée des rectangles de la forme [a, b[×[c, d[, c'est-à-dire que les ouverts de S×S sont les réunions de tels rectangles.

Propriétés

La topologie de S×S est strictement plus fine que la topologie usuelle de ℝ×ℝ. Elle n'est tout de même pas discrète.
S×S est séparable, à bases dénombrables de voisinages et complètement régulier (car S l'est).
Il n'est pas localement compact (car le fermé S×{0} ne l'est pas).
Sa petite dimension inductive $ind(S \times S)$ étant nulle (comme celle de S), il est totalement discontinu.
Il n'est pas de Lindelöf (alors que S l'est). En effet, l'antidiagonale Δ = {(x, –x) | x ∈ ℝ} est un fermé discret non dénombrable.
Par conséquent, il n'est pas à base dénombrable ni σ-compact.
Il n'est pas métrisable car, bien que séparable, il possède un sous-espace non séparable (l'antidiagonale Δ).
S×S n'est pas normal (alors que S est parfaitement normal), puisqu'il est séparable et possède un fermé discret Δ ayant la puissance du continu ou, plus directement, puisque K = {(x, –x) | x ∈ ℚ} et Δ\K sont deux fermés disjoints non séparés (en) par deux ouverts disjoints.

Notes et références

(en) Lynn Arthur Steen et J. Arthur Seebach, Jr., Counterexamples in Topology, Dover, 1995, 244 p. (ISBN 978-0-486-68735-3, lire en ligne)
(en) R. H. Sorgenfrey, « On the topological product of paracompact spaces », Bull. Amer. Math. Soc., vol. 53,‎ 1947, p. 631-632 (lire en ligne)

(en) John L. Kelley, General Topology, Springer, coll. « GTM » (n^o 27), 1975, 298 p. (ISBN 978-0-387-90125-1, lire en ligne)
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Sorgenfrey plane » (voir la liste des auteurs).

Article connexe

Plan de Moore

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.