Partitionnement spectral

Le partitionnement spectral est une méthode de partitionnement en K groupes reposant sur la minimisation d'un critère de type « coupe » (coupe simple à K=2, ou coupe multiple à K≥2). Ces deux mesures expriment la cohésion interne des groupes, relativement à leur dissociation les uns des autres. Elles sont directement fonctions d'une matrice de similarités entre objets, notée S.

Étant donné un ensemble de N objets, il est possible d'obtenir une représentation détaillée de cet ensemble sous la forme d'un graphe pondéré (cf. théorie des graphes), noté G(V,E,S). V désigne l'ensemble des N nœuds du graphe, correspondant aux objets ; E est l'ensemble des arcs inter-nœuds et S est la matrice de poids des arcs (matrice de similarités), symétrique et non négative (S_ij indiquant la similarité entre les objets x_i et x_j).

Exemple de graphe pondéré des données (en rouge, la coupe du graphe souhaitée).

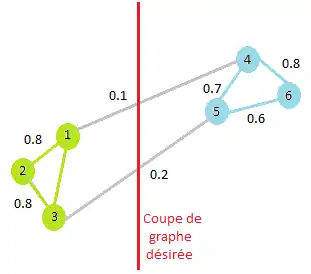
Dans le but de résoudre le problème d'optimisation du critère de coupe défini précédemment, le partionnement spectral s'appuie sur l'utilisation du spectre de la matrice de similarités des données en vue du partitionnement de l'ensemble des objets dans un espace de plus faible dimension. On a alors un problème de partitionnement de graphe pour lequel les nœuds d'un même groupe sont similaires et les nœuds appartenant à des groupes différents sont dissimilaires[1].

L'objectif de la construction d'un graphe pondéré est de rendre compte (ou de modéliser) les relations de voisinage entre les objets. Il existe alors plusieurs façons de procéder :

• Graphe de voisinage ε : connexion des nœuds pour lesquels la similarité S_ij est supérieure à ε,
• Graphe des k plus proches voisins : connexion du i^e nœud avec le j^e nœud si et seulement si l'objet x_j fait partie des k plus proches voisins de l'objet x_i.
• Graphe totalement connecté : connexion de tous les nœuds entre eux et pondération des arcs de liaison par la valeur de S_ij.

Dans la littérature, plusieurs techniques permettent d'obtenir une mesure de similarité entre deux objets. Le choix de la fonction de similarité dépend essentiellement du domaine de provenance des données (par exemple, fouille de documents, fouille de données web, etc.), mais également du type de données (qui peuvent être décrit par des variables numériques, catégorielles, binaires, etc.). Cependant, les deux formules les plus répandues et les plus utilisées sont :

• Noyau Gaussien[2] :

${\displaystyle S_{ij}=\exp \left({-d^{2}(x_{i},x_{j}) \over {2\sigma ^{2}}}\right)}$

avec d étant une mesure de distance (de type Euclidienne, Manhattan, Minkowski, etc.), et σ, un paramètre d'échelle dont la valeur est fixé par l'utilisateur.

• Distance cosinus[3] :

${\displaystyle S=B^{T}B}$

avec B désignant la matrice de données (constituée de N objets décrits chacun par M attributs) normalisée en ligne.

Les algorithmes de partitionnement spectral utilisent l'information contenue dans les vecteurs propres d'une matrice laplacienne (construite à partir de la matrice de similarités S) afin de détecter une structure des données. Soit D, la matrice diagonale des degrés (D=diag(D₁₁,...,D_NN)) telle que :

${\displaystyle {D_{ii}}=\sum _{j=1}^{N}S_{ij}}$

représente le degré du i^e nœud du graphe G. Il est alors possible de construire la matrice laplacienne L en utilisant une des nombreuses normalisations présentes dans la littérature :

• Aucune normalisation[4] :

${\displaystyle {L}=S}$

• Normalisation par division[5] :

${\displaystyle {L}=D^{-1}S}$

• Normalisation par division symétrique[6] :

${\displaystyle {L}=D^{-1 \over 2}SD^{-1 \over 2}}$

• Normalisation additive[7] :

${\displaystyle {L}={(S+d_{max}I-D) \over d_{max}}}$

(avec d_max désignant le degré maximum de D et I étant la matrice identité). L'étape suivante consiste à extraire les vecteurs propres de la matrice laplacienne. Il est démontré que l'utilisation des K (nombre de groupes souhaité) premiers vecteurs propres orthogonaux de L (correspondant aux K plus petites valeurs propres), permet d'obtenir un espace de projection de plus faible dimension (en K dimensions) que l'espace original (en M dimensions). La matrice X est alors construite en stockant ces vecteurs propres (en colonnes) : ${\displaystyle {X}=[x_{1},x_{2},...,x_{K}]}$. Parmi les algorithme de calcul des valeurs propres, on peut citer la méthode de la puissance itérée.

Le partitionnement des données est alors effectué sur la matrice X. En effet, la première étape consiste à considérer chaque ligne de cette matrice comme représentant un objet dans l'espace spectral (en K dimensions). La seconde étape est alors d'appliquer un algorithme de classification non-supervisée sur cette matrice. Le partitionnement des données en K groupes se résume alors à l'affectation de l'objet original x_i au groupe k si et seulement si la i^e ligne de X a été affectée au groupe k.

Bien que l'algorithme de partitionnement utilisé le plus souvent dans la littérature soit l'algorithme des K-moyennes, il est tout à fait envisageable d'utiliser n'importe quelle autre méthode non-supervisée afin de classer les différents objets[8] - [9].

• Indexation et recherche par le contenu[4],
• Recherche de documents Web[10],
• Segmentation d'images[5],
• Analyse de marchés,
• Analyse de documents[11],
• Classification non-supervisée.