Onglet sphérique
En géométrie, un onglet sphérique est le solide découpé dans un boule par deux demi-plans ayant pour frontière le même diamètre. Plus précisément, ces demi-plans découpent dans la boule deux onglets sphériques, un, plus petit qu'un hémisphère, est l'onglet mineur, l'autre est l'onglet majeur.
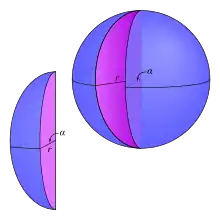
Un onglet sphérique est une portion de boule interceptée par un dièdre dont l'arête passe par le centre de la sphère. Son angle dièdre α et le rayon r de la sphère sont les deux dimensions caractérisant un onglet sphérique.

Un quartier d'orange ou de citron est un exemple d'onglet sphérique.
La surface enfermant l'onglet sphérique est constituée d'un fuseau sphérique et de deux demi-disques.
Propriétés géométriques
Un onglet sphérique possède deux plans de symétrie: le plan médiateur de l'arête du dièdre (dans les cas des fuseaux terrestres c'est le plan équatorial) et le plan bissecteur de l'angle dièdre. Il possède donc un axe de symétrie qui est l'intersection de ces deux plans. L'axe antipodal est le diamètre commun aux deux demi-plans. Un plan perpendiculaire à l'axe antipodal découpe dans l'onglet sphérique des secteurs circulaires
- Volume : où S est l'aire du fuseau servant de base à l'onglet;
- Aire latérale : la surface enfermant l'onglet sphérique est constituée d'un fuseau sphérique et de deux demi-disques donc
- Centre de gravité : le centre de gravité de l'onglet sphérique est au trois quarts du segment joignant le centre de la sphère au centre de gravité du fuseau sphérique[1] soit
Références
- Mémoire de la Société royale des sciences de Liège, t. 6, (lire en ligne), p. 10
Voir aussi
Articles connexes
Lien externe
- (en) Eric W. Weisstein, « Spherical wedge », sur MathWorld







![{\displaystyle Mx={\Big [}\sin \varphi {\Big ]}_{-\alpha /2}^{\alpha /2}\cdot \left[{\frac {\theta }{2}}-{\frac {\sin(2\theta )}{4}}\right]_{0}^{\pi }\cdot \left[{\frac {\rho ^{4}}{4}}\right]_{0}^{r}}](https://img.franco.wiki/i/9b318ada46836b78dc42449311cc32e83cfcff7e.svg)

