Fuseau sphérique
En géométrie, un fuseau sphérique ou digone sphérique est une portion de sphère délimitée par deux demi-grands cercles de mêmes extrémités. Plus précisément ces deux demi-grands cercles découpent deux fuseaux sphériques, l'un, plus petit qu'un hémisphère est appelé le fuseau mineur, tandis que l'autre est qualifié de fuseau majeur.

Par exemple, les fuseaux horaires sont issus (avec ajustement géopolitique) du découpage de la sphère terrestre en 24 fuseaux d'angle de 2π/24 radians soit 15°. En première approximation, la portion de surface de la Lune, éclairée par le Soleil et visible depuis la Terre est un fuseau sphérique et cela explique le nom anglais de cet objet spherical lune.
Un fuseau sphérique est la portion de sphère interceptée par un dièdre dont l'arête passe par le centre du cercle.
Ce même dièdre découpe dans la boule un solide géométrique qui porte le nom d'onglet sphérique.
Lorsque l'angle dièdre est plat, le fuseau sphérique coïncide avec un hémisphère.
Propriétés géométriques
Les dimensions d'un fuseau sphérique sont entièrement déterminées par la donnée du rayon r de la sphère et de l'angle dièdre α, exprimé en radians, qui l'intercepte.
Il possède deux plans de symétrie: le plan médiateur de l'arête du dièdre (dans les cas des fuseaux terrestres c'est le plan équatorial) et le plan bissecteur de l'angle dièdre. Il a donc un axe de symétrie qui est l'intersection de ces deux plans. L'axe antipodal est l'axe joignant les extrémités des deux demi-grands cercles.
- Surface :
- Centre de gravité. Il est situé sur l'axe de symétrie du fuseau. Sa distance au centre est donnée par[1]
- pour un fuseau sphérique d'épaisseur infiniment petite
- pour un fuseau d'angle diédral α, il faut trouver le centre de gravité de l'arc de cercle sur lequel se trouvent tous les centres de gravité des fuseaux d'épaisseur infiniment petite
Pavage et développement de la sphère
Pavage
Tout fuseau d'angle 2π/n permet de générer un pavage régulier de la sphère, pavage que les anglophones appellent hosohedron[2] du grec «hosos» (aussi grand que, aussi nombreux que) et «hedra» (base, face)[3], en relation au fait que ce pavage comporte autant de faces que l'on souhaite.
Développement

Une sphère n'étant pas développable, un fuseau, qui est un élément de pavage de la sphère, ne l'est pas non plus. Cependant, un développement approximatif d'un fuseau assez étroit permet de proposer une bonne approximation d'un développement de la sphère. C'est ce principe qui est utilisé tant dans le simple ballon de plage qu'en aérostation dans la construction des aérostats sphériques[4]. Concernant la représentation plane de chaque fuseau, on propose tantôt d'utiliser des arcs de cercle[5], tantôt des arcs de sinusoïdes[6] - [7]
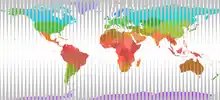
C'est ce même principe de développement qui est utilisé en cartographie dans le développement de la sphère terrestre selon la transverse universelle de Mercator dans laquelle la sphère est découpée en 60 fuseaux, chacun de ces fuseaux étant représenté ensuite suivant une projection de Mercator transverse centrée sur le méridien médian de chaque fuseau.
Références
- Édouard Collignon, Traité de mécanique, vol. 2, Hachette, (lire en ligne), p. 296
- Voir en:Hosohedron
- (en) Steven Schwartzman, The words of mathematics : an etymological dictionary of mathematical terms used in English, Mathematical association of America, (lire en ligne), p. 108
- Thomas Monge, « Calculs de l'enveloppe du ballon à gaz », sur Construction d'un ballon à gaz (consulté le )
- E. Sergent, Traité pratique et complet de tous les mesurages, métrages, jaugeages de tous les corps, vol. 1, Lacroix, (lire en ligne), p. 468
- Raoul Marquis et Henry Graffigny, Traité d'aérostation: théorique et pratique, Baudry et cie, (présentation en ligne), pp.2 et 3
- Daniel Jaques et Jean-François Calame, Géométrie spatiale : Le vade-mecum, PPUR Presses polytechniques, (présentation en ligne), p. 267