Onde mécanique progressive

Une onde mécanique progressive est le phénomène de propagation d'une perturbation locale dans un milieu matériel[1]. Si elle est de plus périodique, la caractéristique principale de l'onde progressive est que la perturbation se retrouve identique à elle-même après une durée T (période temporelle de propagation) et à une distance de lambda (période spatiale de propagation ou longueur d'onde). Il faut pour cela que le milieu de propagation ait une extension infinie ou, tout du moins, une taille très grande devant celle de la longueur d'onde. Dans le cas contraire, sous certaines conditions liant la dimension du milieu et la longueur d'onde, il s'établit une onde stationnaire. C'est le cas du confinement, par exemple dans le cas d'une corde vibrante fixée aux deux extrémités, l'onde émise se voit superposée à l'onde réfléchie ce qui donne naissance, grâce au théorème de superposition des ondes, à une onde stationnaire vibrant selon des modes propres précis : la longueur entre les extrémités doit être un multiple entier de la demi-longueur de l'onde[2].

Lors de la propagation d'une onde mécanique, il y a un « transport d'énergie sans transport de matière » ; cela signifie simplement que l'intensité de la perturbation peut s'exprimer sous la forme d'une énergie. Par exemple, si l'on met de l'air sous pression dans un tube, on peut exprimer cette compression sous la forme d'une énergie élastique ; si l'on transporte le tube, on a donc un « transport d'énergie avec transport de matière ». Mais si l'on crée une surpression locale (par exemple en ouvrant brutalement le tube), alors cette surpression va se propager, mais sans créer de vent ; l'air sera resté sur place mais la pression se sera déplacée, on a donc un « transport d'énergie sans transport de matière ».

Célérité

La célérité d'une onde est une propriété du milieu de propagation. Tout point du milieu de propagation reproduit avec un certain retard, la perturbation imposée par la source.

$v={\frac {d}{t}}$
Dans le Système international :

v, célérité de l'onde en mètre par seconde (m/s)
d, distance parcourue par l'onde en mètre (m)
t, temps pendant lequel l'onde a parcouru la distance d en seconde (s)

Les ondes progressives périodiques

Une onde mécanique progressive périodique est une onde mécanique dont le mouvement de la source est périodique, c'est-à-dire qu'il se répète au bout du temps T. Exemple d'une corde : On bouge une corde toutes les x secondes
Ici, T = x On mesure la période en secondes.
Cette période est la plus petite durée au bout de laquelle un point de cette corde subit la même déformation. La période est liée à la fréquence par la formule $f=1/T$ .

Schéma longueur d’onde

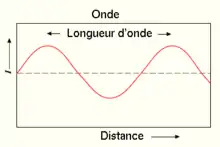
La déformation peut être la même sur deux points de la corde, on dit alors que ces deux points sont en phase. Si l'on mesure l'écart entre deux points en phase les plus proches, on obtient la longueur d'onde λ. Deux points vibrant en phase sont séparés d'une distance multiple entier de la longueur d'onde.

Il existe un rapport entre la longueur d'onde λ, la période T et la vitesse de propagation v des ondes mécaniques périodiques, il s'agit de $\lambda =v*T$ .

On associe également à chaque point de la corde une fréquence de vibration notée f qui s'exprime en hertz : $\lambda =v/f$ .

Ondes transversales et ondes longitudinales

Ondes transversales

Une onde transversale est provoquée par une perturbation qui est perpendiculaire à la direction de propagation de l'onde. C'est le cas notamment d'une onde à la surface de l'eau. Le mouvement d'une corde tendue entre deux points fixes est quant à lui une onde stationnaire transversale.

Ondes longitudinales

Une onde longitudinale est provoquée par une perturbation dont la direction est parallèle à la direction de propagation de l'onde.

exemples :

onde produite par le relâchement brutal d'un élastique étiré
propagation d'une onde sur un ressort tendu
propagation d'un son

Exemple d'ondes mécaniques

Notes et références

Marie-Noëlle Sanz, Stéphane Cardini, Elisabeth Ehrhard, Annie Guerillot, et al., Physique tout-en-un PSI-PSI*, J'intègre, DUNOD, 2014
Christian GARING, Ondes mécaniques et diffusion, Ellipses, 1998, 238 p.

Voir aussi

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.