Noyau de Fejér

Tracé des noyaux de Fejér à différents ordres.

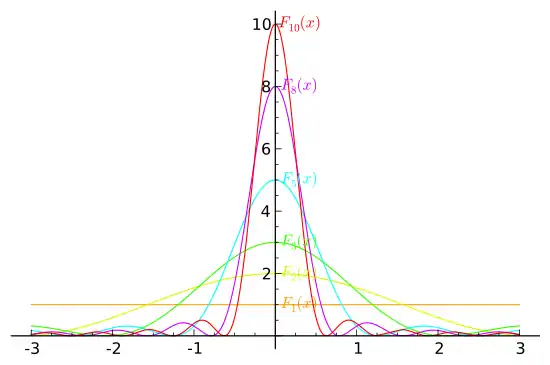
Le noyau de Fejér est la suite (F_n)_n∈ℕ* de fonctions analytiques dont le terme de rang n, appelé noyau de Fejér d'ordre n, est la moyenne arithmétique des n premiers noyaux de Dirichlet :

${\displaystyle \forall x\in \mathbb {R} \quad F_{n}(x)={\frac {1}{n}}\sum _{k=0}^{n-1}D_{k}(x)}$.

En développant la définition ci-dessus, les deux expressions classiques du noyau de Dirichlet donnent respectivement :

1. ${\displaystyle F_{n}(x)={\frac {1}{n}}\left({\frac {\sin {\frac {nx}{2}}}{\sin {\frac {x}{2}}}}\right)^{2}}$ si ${\displaystyle x\notin 2\pi \mathbb {Z} }$ (donc, par continuité, F_n(x) = n si x est un multiple entier de 2π) ;
2. ${\displaystyle F_{n}(x)=\sum _{k=-n}^{n}\left(1-{\frac {|k|}{n}}\right)\mathrm {e} ^{\mathrm {i} kx}}$.

On obtient la somme de Fejér d'ordre n d'une fonction f (intégrable sur [–π, π] et 2π-périodique) en effectuant un produit de convolution de f par le noyau de Fejér.

Le noyau de Fejér est un noyau de sommabilité positif sur ${\displaystyle \mathbb {R} /2\pi \mathbb {Z} }$, c'est-à-dire que :

• ${\displaystyle \forall n\in \mathbb {N} ^{*}\quad F_{n}\geq 0}$ ;
• ${\displaystyle \forall n\in \mathbb {N} ^{*}\quad {\frac {1}{2\pi }}\int _{-\pi }^{\pi }F_{n}(x)\,\mathrm {d} x=1}$ ;
• ${\displaystyle \forall \varepsilon >0\quad \lim _{n\to \infty }\int _{\pi \geq |x|>\varepsilon }|F_{n}(x)|\,\mathrm {d} x=0}$.

La suite (F_n) est donc une approximation de l'unité de l'algèbre de Banach ${\displaystyle \mathrm {L} ^{1}(\mathbb {R} /2\pi \mathbb {Z} )}$ (munie de produit de convolution).